The ideal gas laws show the correlation of the temperature, pressure, volume, and the amount of a gas. It is derived from the individual gas laws such as the Boyle’s law, Charles’ law, etc. Remember, when discussing those, we used a pump with a freely moving plunger and by changing the parameters one by one, we were able to get the following correlations:
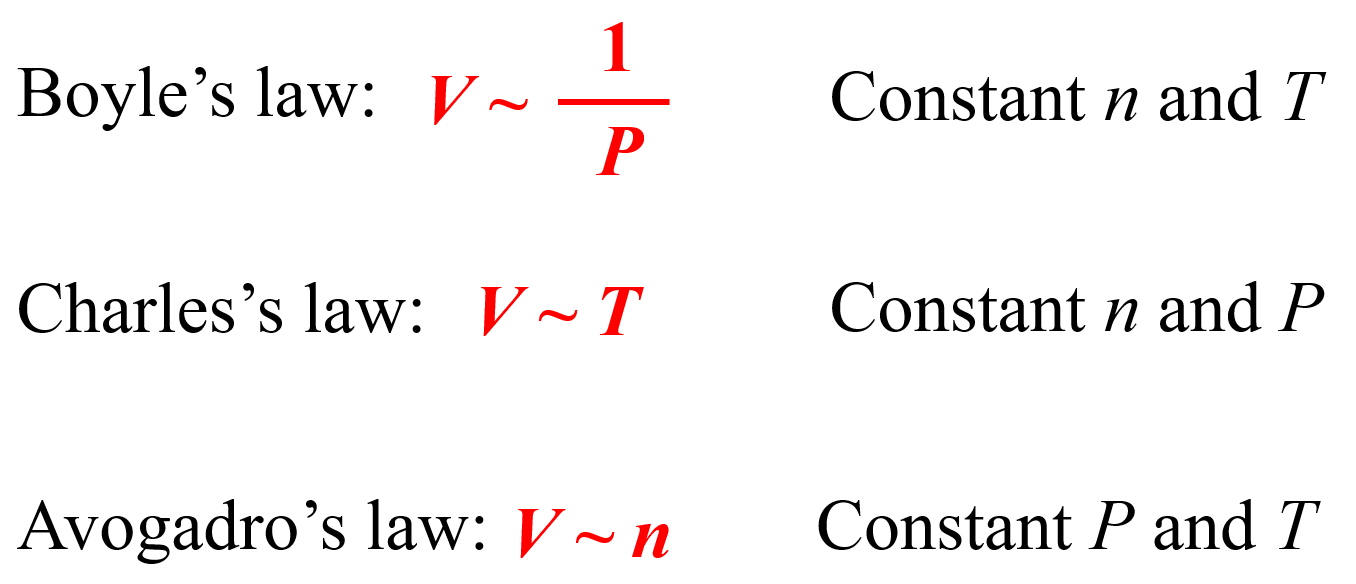
We can combine all of these to get an expression showing how, for example, the volume of an ideal gas is correlated to the temperature, pressure, and the moles of the gas:
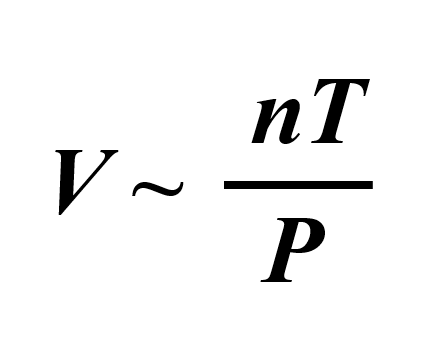
To bring in the equal sign, we introduce a constant:
This can be explained using the example of a car dealership income. The income depends on the number of sales which we can represent as:
income ~ number of cars sold
However, we cannot say income = number of cars sold, so to switch an equal sign, we need to introduce a constant. This can be the price of the car transforming the equation to:
Income = price x number of cars
Now, for the parameters of ideal gases, the constant is the R, which is called the ideal gas constant.
\[V\;{\rm{ = }}\,R\, \times \,\frac{{nT}}{P}\]
By rearranging it, we obtain the ideal gas law equation:
Again, R is called the ideal gas constant. Although it has different values and units, you will mostly be using this:
\[R\;{\rm{ = }}\;{\rm{0}}{\rm{.08206}}\;\frac{{{\rm{L}} \cdot {\rm{atm}}}}{{{\rm{mol}} \cdot {\rm{K}}}}\]
The Ideal Gas Law in Problems
The ideal gas law equation is used when you need to find P, V, T, or n, for the system where they do not change.
For example, A sample of hydrogen gas is added into a 5.80 L container at 56.0 °C. How many moles of the gas are present in the container if the pressure is 6.70 atm?
Rearrange the ideal gas law to get an expression for the moles (n):
PV = nRT
\[{\rm{n}}\;{\rm{ = }}\;\frac{{{\rm{PV}}}}{{{\rm{RT}}}}\]
Now, before entering the numbers, remember to always convert the temperature to Kelvin whenever solving a gas problem:
T = 56.0 oC + 273 = 329 K
And now, we can plug in the numbers:
\[{\rm{n}}\;{\rm{ = }}\;\frac{{{\rm{6}}{\rm{.70}}\;\cancel{{{\rm{atm}}}}\; \times \;{\rm{5}}{\rm{.80}}\;\cancel{{\rm{L}}}}}{{{\rm{0}}{\rm{.08206}}\;\cancel{{\rm{L}}}\;\cancel{{{\rm{atm}}}}\;\cancel{{{{\rm{K}}^{{\rm{ – 1}}}}}}\;{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}{\rm{ }} \times \;{\rm{329}}\;\cancel{{\rm{K}}}}}\; = \;1.44\;{\rm{mol}}\]
Molar Mass and Density of Gases
Density and molar mass are calculated by modifying the ideal gas law equation. What we do is first replace the moles (n) in PV = nRT with mass over the molar mass:
Next, we rearrange this formula to bring the V under the m which is the density of the gas (mass/volume = density):
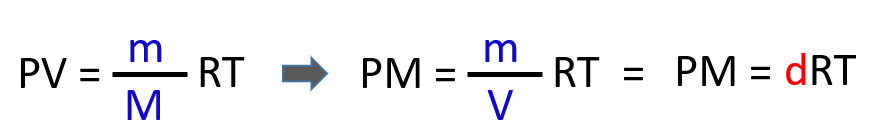
From this equation, we can obtain an expression for the density and molar mass of an ideal gas:
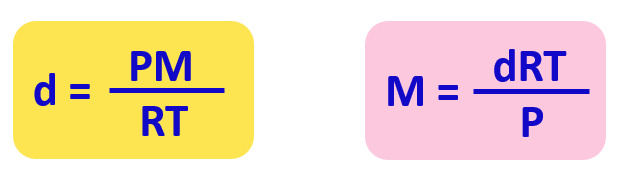
Check this article for details and some examples of determining the molar and the density using the ideal gas law equation.
How do I know which gas law to use?
When the problem has varying parameters, then instead of trying to figure out which gas law to use, you can go with the combined gas law equation:
Let’s keep it for another article because there is quite a lot of information in this one.
Here are some summary of gas law problems and if you are not sure how to start, make sure to check the articles on the gas law chapter.
Practice
A 3.00-L bulb containing N2 at 1.80 atm pressure is connected to a 2.00-L bulb filled with H2 at 3.50 atm pressure. What is the final pressure of the system when the valve is opened?
Sodium azide is used in automobile airbags as a source of nitrogen gas to rapidly inflate the bags upon a hit. If the volume of the airbag is 7.95 L, what mass of NaN3 is required to produce enough nitrogen to fill it at 23.0 °C and 1.20 atm?
2NaN3(s) → 2Na(s) + 3N2(g)
In a particular reaction, at 25 °C, 16.4 L of carbon monoxide at a 950.0 torr is mixed with 11.2 g of iron (III) oxide, and 5.68 g iron is obtained. What is the percent yield of the reaction?
Fe2O3 + 3CO(g) → 2Fe + 3CO2(g)