The Avogadro’s Law studies the correlation between the amount of the gases (mole) and the volume of an ideal gas. To demonstrate it, we can use a pump equipped with a freely moving plunger that is filled with an ideal gas.
The idea is simple: as we pump in some gas into the system, the plunger, as expected starts moving up indicating that the volume of the gas increases:
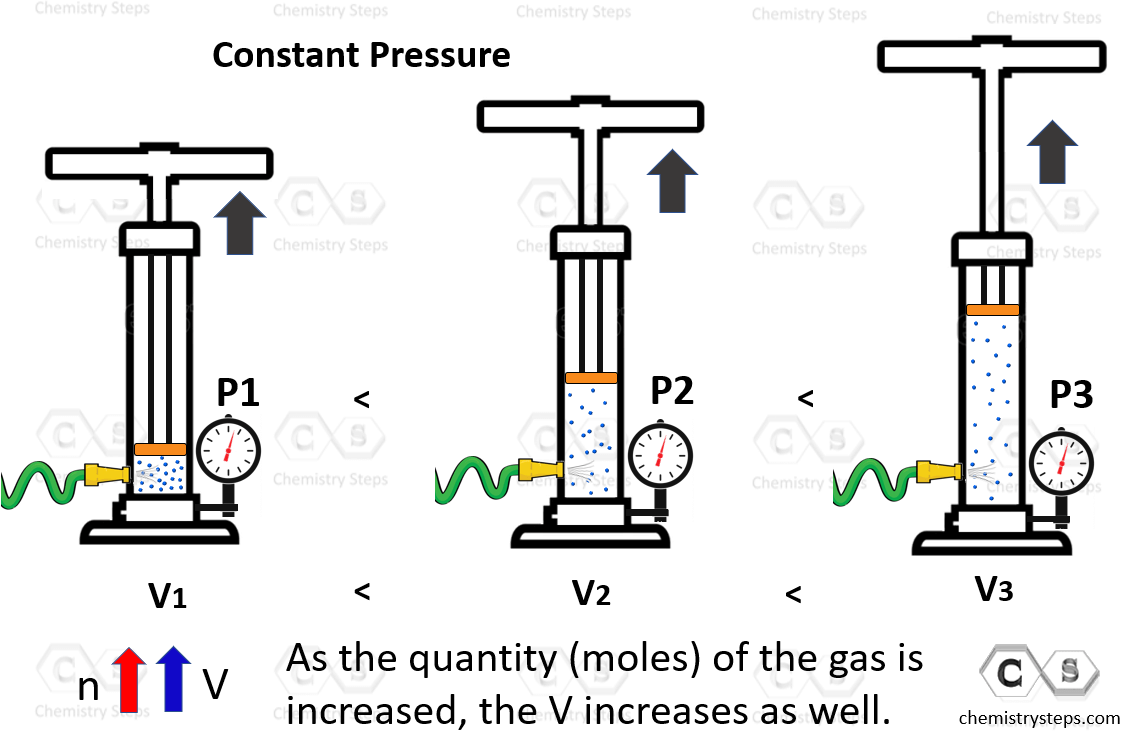
Notice that the pressure of the system remains constant as the plunger can freely move with the expanding of the gas. This experiment demonstrates that the volume of a gas is directly proportional to its number of moles. In other words, the more gas, the larger the volume which again is a very intuitive observation.
V ~ n
To bring in the equal sign instead of the proportional sign, we introduce a constant:
V = constant x n
This can be explained using the example of a car dealership income. The income depends on the number of sales which we can represent as:
Income ∼ number of cars
However, we cannot say income = number of cars sold, so to switch an equal sign, we need to introduce a constant. This can be the price of the car transforming the equation to:
Income = price x number of cars
So, for our experiment, we are not interested too much in the constant, but rather in how it links the volume and the amount of the gas at positions 1 and 2. If we rearrange the equation with the constant, we can write that:
\[\frac{{\rm{V}}}{{\rm{n}}}\;{\rm{ = }}\,{\rm{constant}}\]
Because the ratio V/n is constant, we can write that:
\[\frac{{{{\rm{V}}_{\rm{1}}}}}{{{{\rm{n}}_{\rm{1}}}}}\;{\rm{ = }}\,{\rm{constant}}\,{\rm{ = }}\,\frac{{{{\rm{V}}_{\rm{2}}}}}{{{{\rm{n}}_{\rm{2}}}}}\]
Omitting the constant, we obtain the following formula:
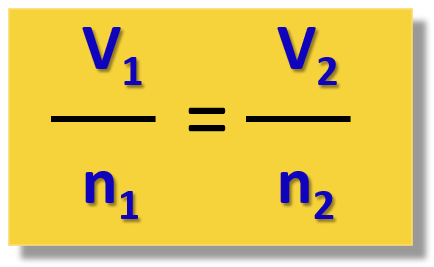
This is the practical implication of the Avogadro’s law that is used for solving gas problems.
For example, what is the volume of 0.451 mol of nitrogen gas if at the same temperature 1.25 mole of it occupies 24.8 L volume?
First, write down the data given in the problem:
n1 = 0.451 mol
n2 = 1.25 mol
V2 = 24.8 L
V1 = ?
We need to rearrange the Avogadro’s law to get an expression for V1.
\[\frac{{{{\rm{V}}_{\rm{1}}}}}{{{{\rm{n}}_{\rm{1}}}}}\;{\rm{ = }}\,\frac{{{{\rm{V}}_{\rm{2}}}}}{{{{\rm{n}}_{\rm{2}}}}}\]
\[{{\rm{V}}_{\rm{1}}}\,{\rm{ = }}\,\frac{{{{\rm{n}}_{\rm{1}}}{{\rm{V}}_{\rm{2}}}}}{{{{\rm{n}}_{\rm{2}}}}}\]
\[{{\rm{V}}_{\rm{1}}}\,{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.451}}\,\cancel{{{\rm{mol}}}}\,{\rm{ \times }}\,{\rm{24}}{\rm{.8}}\,{\rm{L}}}}{{{\rm{1}}{\rm{.25}}\,\cancel{{{\rm{mol}}}}}}\,{\rm{ = }}\,{\rm{8}}{\rm{.95}}\,{\rm{L}}\]
The answer is reasonable because, as expected, the volume of 0.451 mol gas is smaller than that of 1.25 mol.
The Ideal Gas Law
Notice that in the experiment, we made an assumption that the pressure is constant, and this is what we also do the other gas laws to determine the desired correlation. For example, in the Boyle’s law, we study a constant amount of gas at constant temperature and find that the pressure increase as the volume is decreased.
To combine all the laws together and have the four variables (n, P, V, T) in one place, the Ideal Gas Law equation is obtained:

The R is called the ideal gas constant. Although it has different values and units, you will mostly be using this:
\[R\;{\rm{ = }}\;{\rm{0}}{\rm{.08206}}\;\frac{{{\rm{L}} \cdot {\rm{atm}}}}{{{\rm{mol}} \cdot {\rm{K}}}}\]
The ideal gas law equation is used when you need to find P, V, T, or n, for the system where they do not change.
We will cover the ideal gas law in a separate post with some examples.
How do I know which gas law to use?
You are probably wondering about this question now that every gas law brings a new equation. For this, there is what is called the combined gas law and as long as you remember it, you do not need to remember all the gas laws to solve a problem.
Let’s keep it for another article because there is quite a lot of information in this one.
The Molar Volume of Ideal Gases
Talking of the volume and the moles of a gas, remember that at STP, one mole of any gas occupies a volume of 22.4 L called the molar volume, Vo.
This is because in ideal gases, the size of molecules is very small compared to the intermolecular distances. So, most of the volume is almost empty, and therefore, it does not matter what gas it is, the volume is determined to be 22.4 L at 0 oC and 1 atm.
Check Also
- Boyle’s Law
- Charle’s Law
- Gay-Lussac’s Law
- The Ideal Gas Law
- Celsius or Kelvin
- Ideal-Gas Laws
- Combined Gas Law Equation
- How to Know Which Gas Law Equation to Use
- Molar Mass and Density of Gases
- Graham’s Law of Effusion and Diffusion
- Graham’s Law of Effusion Practice Problems
- Dalton’s Law of Partial Pressures
- Mole Fraction and Partial Pressure of the Gas
- Gases in Chemical Reactions
- Gases-Practice Problems
