Hess's law state function diagram explanation

General Chemistry

Hess’s law allows measuring the enthalpy change (ΔH) for a reaction without making calorimetric measurements. To do this, we need the enthalpies of some other reactions.

For example,

Using the given data for reactions (1) and (2), calculate the ΔH for the reaction:

 

2NO2(g) + Cl2(g) → 2NOCl(g) + O2(g), ΔH = ?

 __________________________________________________

1) 2NO(g) + Cl2(g) → 2NOCl(g), ΔH = -76 kJ

2) 2NO(g) + O2(g) → 2NO2(g), ΔH = -114 kJ

 

To find the ΔH for the target reaction, we need to modify equations 1 and 2 such that we add them together and get the target equation.

 

Of course, by doing so, we need to follow rules for manipulating thermochemical equations:

 

  • If the equation is multiplied by any factor, the ΔH must be multiplied by the same factor.
  • If the equation is reversed, the sign of ΔH must be changed.

 

So, to get the target equation, first look up which of its components appear in the equations with known ΔH (equations 1 and 2).

NO2 is the first reactant in the target equation, and it appears in equation (2) as a product. Therefore, reverse the second reaction to make NO2 a reactant like in the target reaction. Let’s label the new equation as (2a). Make sure to change the sign for ΔH:

 

2a) 2NO2(g) → 2NO(g) + O2(g), ΔH = +114 kJ

 

Pay attention to the coefficient as well; in both the target and (2a) equations, we have 2 NO2 and this is what you want. The component in the reference equation most often needs to have the same coefficient as in the target equation.

The Cl2, on the other hand, is a reactant in the target equation and so is it in equation (1), therefore, we keep equation (1) intact.

At this point, we can add equations (1) and (2a) to see if we get the target equation. Remember to add the enthalpies with correct signs as well:

 

1) 2NO(g) + Cl2(g) → 2NOCl(g), ΔH = -76 kJ

+

2a) 2NO2(g) → 2NO(g) + O2(g), ΔH = +114 kJ

__________________________________________

2NO(g) + Cl2(g) + 2NO2(g) → 2NOCl(g) + 2NO(g) + O2(g)

ΔH = -76 kJ + 114 kJ = +38 kJ

 

Cancel any molecules with the same coefficient that appear on both sides of the equation. In this case, it the NO:

 

2NO(g) + Cl2(g) + 2NO2(g) → 2NOCl(g) + 2NO(g) + O2(g)

 

The final equation is:

 

2NO2(g) + Cl2(g) → 2NOCl(g) + O2(g)  ΔH = +38 kJ

 

And this matches the target equation, therefore, the ΔH was determined correctly.

 

How does Hess’s Law Work?

The secret souse of Hess’s law is that enthalpy is a state function, and therefore, ΔHrxn is the same whether the reaction takes place in one step or in a series of steps.

Remember, a state function is a variable that only depends on the initial and final states and not how it was achieved. For example, altitude is a state function and wouldn’t matter how two hikers meet at a 500 ft altitude. One may be on his way to the top, and the other going back having behind a longer walk distance:

 

 

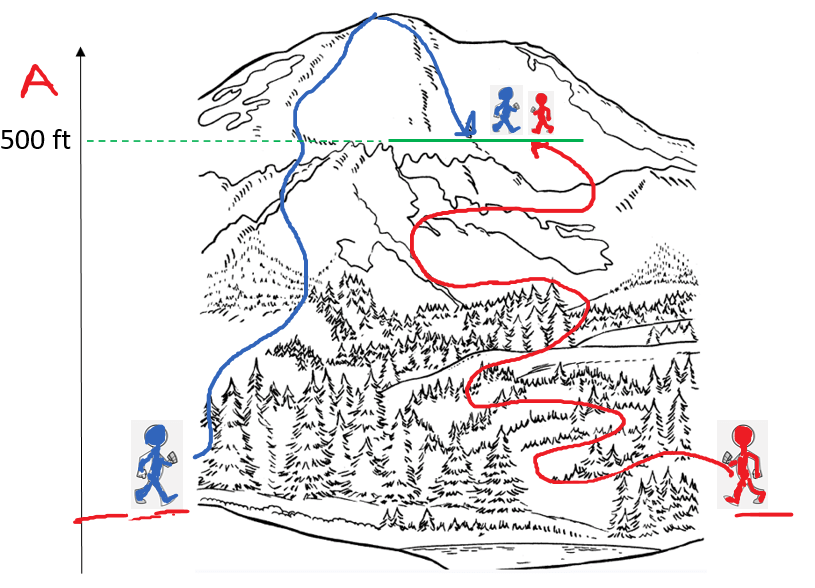
Now, by the same analogy, suppose we need to determine the enthalpy of the reaction 2A + B → 2D, given the enthalpies of the other two reactions:

 

2A + B → 2D ΔH = ?
_____________________

2A + B  →  C ΔH = +50 kJ

C  →  2D ΔH = -80 kJ

 

On an energy diagram, the objective is to go from  “2A + B” to “2D”, but we cannot directly measure the enthalpy change of this process. However, we know that if “2A + B” goes to C, it is +50 kJ, and “C” going to “2D” is -80 kJ.

 

 

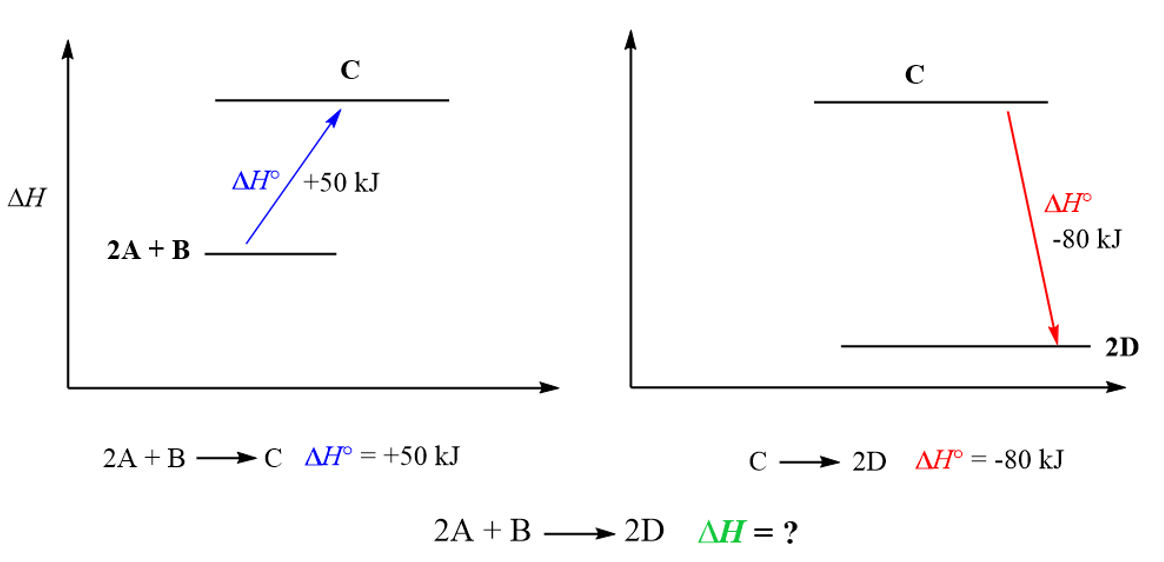
And because enthalpy is a state function, it does not matter how “2A + B” goes to “2D”, so we add the enthalpy changes for these two routes/reactions to find the enthalpy change for going “2A + B” to “2D” directly:

 

 

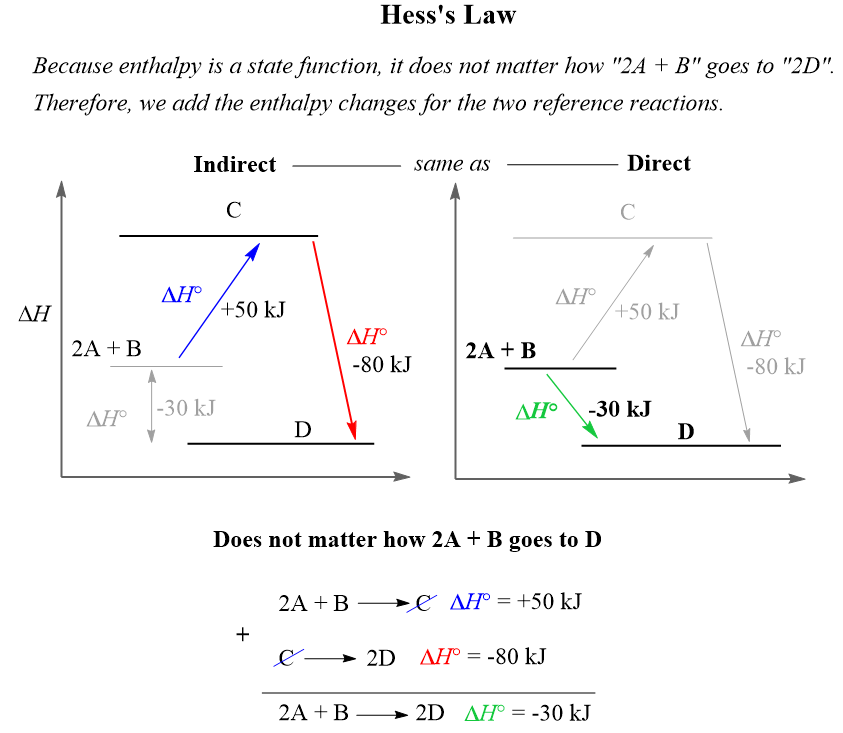
So, to summarize, when solving a problem on the Hess’s law, remember your objective is to manipulate the reference equations such that when you add them up, the target equation is obtained. Remember, to multiply all the coefficients and the ΔH when needed, and to change the sign of ΔH when the equation is reversed.

 

Check Also

Practice

1.

Calculate the enthalpy for the oxidation of CO to CO2 using the enthalpy of reaction for the combustion of C to CO (ΔH = -221.0 kJ) and the enthalpy for the combustion of C to CO2 (ΔH = -393.5 kJ).

2CO(g) + O2(g)  →  2CO2(g)  ΔH = ?

C(s) + O2(g)  →  CO2(g)  ΔH = -393.5 kJ

2C(s) + O2(g)  →  2CO(g)  ΔH = -221.0 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
2.

Calculate the enthalpy for the combustion reaction of sulfur to sulfur trioxide using the enthalpies of the two reactions shown below:

2S(s) + 3O2(g)  →  2SO3(g)  ΔH = ?

S(s) + O2(g)  →  SO2(g)  ΔH = -297 kJ

2SO3(g)  → 2SO2(g) + O2(g)  ΔH = 198 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
3.

Using the Hess’s law, calculate ΔHo for the combustion reaction of butene:

C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(l), ΔHo = ?

Use the following reactions and given ΔH’s:

1) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ

2) C4H8(g) + H2(g) → C4H10(g), ΔHo = -126 kJ

3) 2C4H10(g) + 13O2(g) → 8CO2(g) + 10H2O(l), ΔHo = -5754 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
4.

Using the Hess’s law and the enthalpies of the three combustion reactions below, calculate the enthalpy of the reaction producing methanol (CH3OH) from carbon monoxide and hydrogen gas.

CO(g) + 2H2(g) → CH3OH(g), ΔH = ?

1) 2CO(g) + O2(g) → 2CO2(g), ΔH = -566 kJ

2) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ

3) 2CH3OH(g) + 3O2(g) → 2CO2(g) + 4H2O(g), ΔHo = −1430 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
5.

Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the combustion reaction of CH3Cl:

CH3Cl(g) + O2(g) → CO(g) + HCl(g) + H2O(l), ΔH = ?

1) CO(g) + 2H2(g) → CH3OH(g), ΔHo = -139 kJ

2) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ

3) CH3OH(g) + HCl(aq) → CH3Cl(g) + H2O(l), ΔHo = -28 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
6.

Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the following oxidation reaction of ammonia:

4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g), ΔH = ?

1) N2(g) + 3H2(g) → 2NH3(g), ΔH = -92 kJ

2) 2H2(g) + O2(g) → 2H2O(g), ΔH = -484 kJ

3) N2(g) + O2(g) → 2NO(g), ΔH = 181 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
7.

Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the following oxidation reaction between CuO and HCl:

2CuO(s) + 4HCl(g) → 2CuCl(s) + Cl2(g) + 2H2O(g), ΔH = ?

1) CuO(s) + H2(g) → Cu(s) + H2O(g), ΔH = -85 kJ

2) 2Cu(s) + Cl2(g) → 2CuCl(s), ΔH = -274 kJ

3) H2(g) + Cl2(g) → 2HCl(g), ΔH = -184 kJ

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  

Leave a Comment