In the previous post, we talked about heat capacity, specific heat, and the formula for the relationship between these and the change in temperature.
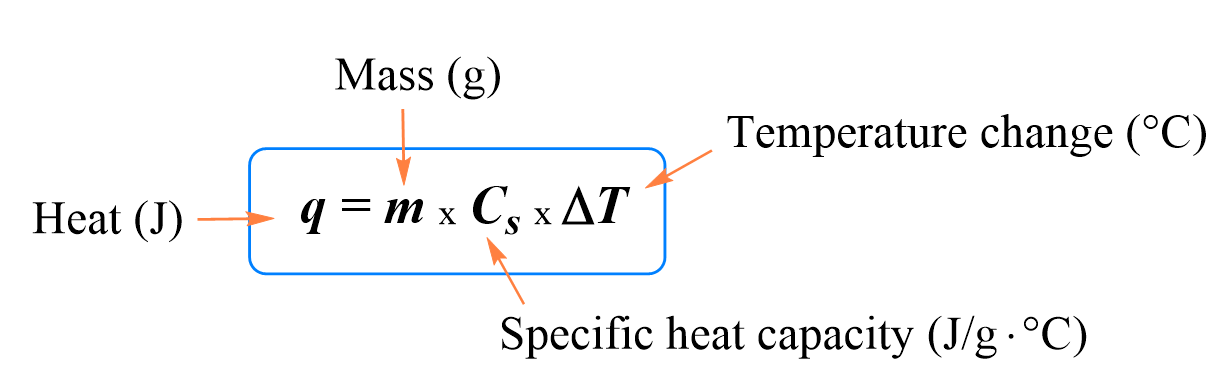
Below are some additional practice examples of heat capacity problems.
When solving a problem related to heat capacity and heat transfer, remember that most of the time, it is assumed the heat is not lost, and it only flows from the object with a higher temperature to the colder one:

The second expression adding the lost and gained heat is easier to use because you do not need to remember which one has a negative sign.
1.
How much heat does it take to increase the temperature of a 540.6-g sample of Fe from 20.0 °C to 84.3 °C? The specific heat of iron = 0.450 J/g °C.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
2.
Calculate the specific heat capacity of a metal if a 17.0 g sample requires 481 J to change the temperature of the metal from 25.0 °C to 67.0 °C?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
3.
Calculate the energy of combustion for one mole of butane if burning a 0.367 g sample of butane (C4H10) has increased the temperature of a bomb calorimeter by 7.73 °C. The heat capacity of the bomb calorimeter is 2.36 kJ/ °C.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
4.
How many joules of energy is required to melt 40.0 g of ice at 0 °C? The heat of fusion (ΔHfus) for ice is 334.0 J/g.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
5.
How many kJ of energy does it take to change 36.0 g of ice at -15.0 °C to water at 0. °C ? The specific heat of ice is 2.10 J/g°C and the heat of fusion (ΔHfus) for ice is 334.0 J/g.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.


