Different objects require a different amount of heat to increase their temperature. For example, if you heat a beaker with 100 g of water and a 100-g iron plate, the latter will reach a high temperature a lot faster than the water.
This is due to what is called heat capacity (C). The heat capacity of a substance is the amount of heat required to raise the temperature of a given quantity of the substance by one degree Celsius. There are two cases when the heat capacity is given to a specific amount of the material:
- Specific heat capacity (Cs) is the amount of heat required to raise the temperature of 1 gram of the substance by 1 °C. (C or S are often used instead of Cs for specific heat capacity).
- Molar heat capacity is the amount of heat required to raise the temperature of 1 mole of a substance by 1 °C.
The specific heat capacity is shown interchangeably as C, Cs, or S.
The specific heat capacity of iron and water are 0.449 J/g · oC and 4.18 J/g · oC respectively. The smaller heat capacity of iron means that it takes less heat to increase the temperature by 1 oC than water does.
Regardless of what material is used, it is determined experimentally that the temperature change is directly proportional to the heat absorbed by the material: q ∝ ΔT.
The constant of proportionality between the temperate change and the absorbed heat is the heat capacity:
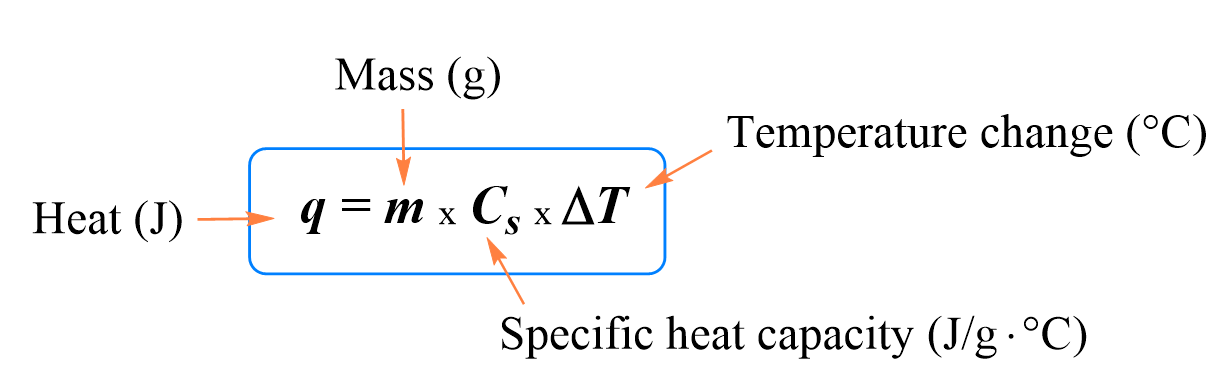
Example:
A 356-g sample of water is heated from 15.0 °C to 84.0 °C. Calculate the amount of heat absorbed (in kilojoules) by the water.
The specific heat capacity of iron is 0.449 J/g · oC, and all we need to do is plug the numbers:
\[q\; = \;mC\Delta T\; = \,{\rm{356}}\;\cancel{{\rm{g}}}{\rm{ \times 0}}{\rm{.449}}\;\frac{{\rm{J}}}{{\cancel{{\rm{g}}}\,\cancel{{^{\rm{o}}{\rm{C}}}}}}\, \times (84.0\, – \;15.0)\,\cancel{{^{\rm{o}}{\rm{C}}}}\; = \;11.0\, \times \,{10^3}\,{\rm{J}}\]
And one last step is to convert the J to kJ:
\[{\rm{11}}{\rm{.0}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{3}}}\,{\rm{J}}\,{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{kJ}}}}{{{\rm{1000}}\,{\rm{J}}}}\;{\rm{ = }}\;{\rm{11}}{\rm{.0}}\;{\rm{kJ}}\]
Mixing Hot and Cold Samples
Another type of problem, related to heat capacity is finding the final temperature when hot and cold water samples are mixed.
For example,
What is the final temperature when a 40 g sample of water at 90 °C is mixed with a 60 g sample at 25 °C?
When mixing any samples at different temperatures, the system goes to final temperature that is in between the temperature of the hot and cold samples. What happens is the heat transfers from the hot to the cold sample:
The basis of solving this problem is the assumption that there is no heat lost to the surroundings and therefore, qgained = –qlost.
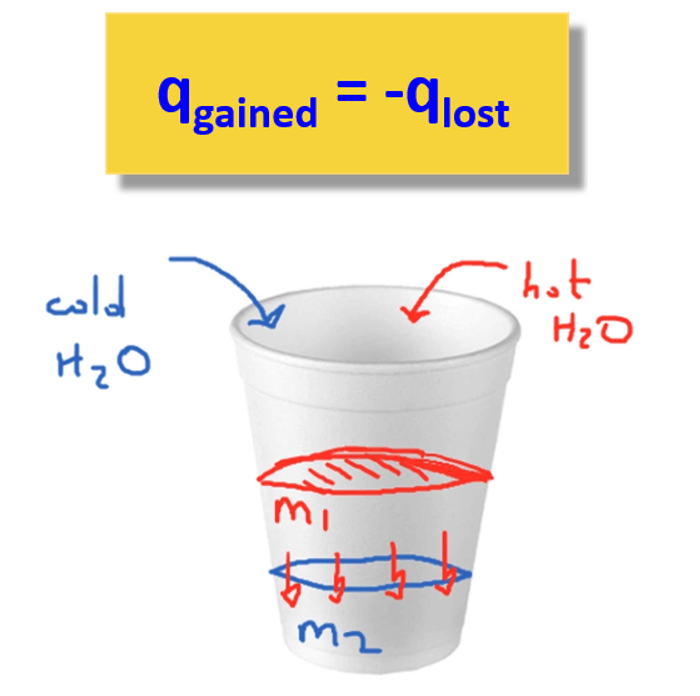
The heat flows from the warmer sample (qlost) to the cooler one (qgained), and the amount of heat lost by the warmer sample is equal to the amount of heat gained by the cooler sample.
We can also write the heat transfer as qlost + qgained = 0 or
q1 + q2 = 0
For our problem, q1 = mCΔT1 , q2 = mCΔT2
so, m1CΔT1 + m2CΔT2 = 0
Let’s assign “1” for the notation of the warmer water sample, and “2” for the colder sample. The temperature changes then would be:
ΔT1 = Tf – 90, and ΔT2 = Tf – 25
Where Tf is the final temperature of the system, so it is the same for the worm and cold samples.
Plug in the numbers and solve for Tf in the following equation:
40 g x C x (Tf – 90) + 60 g x C x (Tf – 25) = 0
Because C (heat capacity of water) appears on both sides of the equation and can be canceled out.
40 g x (Tf – 90) + 60 g x (Tf – 25) = 0
Tf = 51 °C
Notice that the equation can also be set up by using kelvin (K).
A Metal in Water
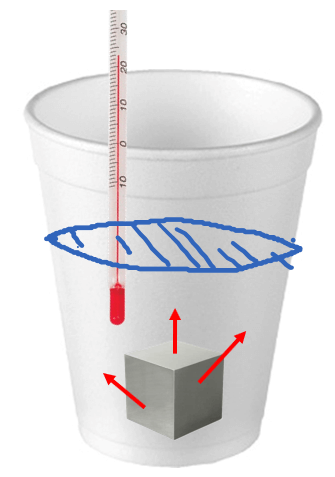 A styrofoam coffee cup contains 150 grams of water at 23.0 oC. A 45.0-gram block of silver metal is heated to 100.0 oC and then placed in the water in the cup. The contents of the cup come to a final temperature of 24.3 oC. What is the specific heat capacity of silver?
A styrofoam coffee cup contains 150 grams of water at 23.0 oC. A 45.0-gram block of silver metal is heated to 100.0 oC and then placed in the water in the cup. The contents of the cup come to a final temperature of 24.3 oC. What is the specific heat capacity of silver?
Remember, again, all the problems in thermochemistry are based on the principle that the heat is not lost, and it only flows from the object with a higher temperature to the colder one:

The second expression adding the lost and gained heat is easier to use because you do not need to remember which one has a negative sign.
So, what we do is write the formula correlating the heat and heat capacity for both water and silver samples, added to make a zero:
150 g x 4.18 J/g oC x (24.3 oC – 23.0 oC) + 45 g (X J/g oC) x (24.3 oC – 100.0 oC) = 0
q (water) q (silver)
Let’s write the equation without the units:
250 x 4.18 x (24.3 – 23.0 ) + 45 (X) x (24.3 – 100.0) = 0
15236.1 – 14421 + 1093.5X – 4500X = 0
815.1 – 3406.5X = 0
X = 815.1/3406.5 = 0.239
Therefore, the calculated specific heat capacity of silver is 0.239 J/g oC.
Practice
How much heat does it take to increase the temperature of a 540.6-g sample of Fe from 20.0 °C to 84.3 °C? The specific heat of iron = 0.450 J/g °C.
Calculate the specific heat capacity of a metal if a 17.0 g sample requires 481 J to change the temperature of the metal from 25.0 °C to 67.0 °C?
Calculate the energy of combustion for one mole of butane if burning a 0.367 g sample of butane (C4H10) has increased the temperature of a bomb calorimeter by 7.73 °C. The heat capacity of the bomb calorimeter is 2.36 kJ/ °C.
How many joules of energy is required to melt 40.0 g of ice at 0 °C? The heat of fusion (ΔHfus) for ice is 334.0 J/g.
How many kJ of energy does it take to change 36.0 g of ice at -15.0 °C to water at 0. °C ? The specific heat of ice is 2.10 J/g°C and the heat of fusion (ΔHfus) for ice is 334.0 J/g.
Check Also
- Energy Related to Heat and Work
- Endothermic and Exothermic Processes
- Heat Capacity Practice Problems
- What is Enthalpy
- Constant-Pressure Calorimetry
- Bomb calorimeter – Constant Volume Calorimetry
- Stoichiometry and Enthalpy of Chemical Reactions
- Hess’s Law and Enthalpy of Reaction
- Hess’s Law Practice Problems
- Standard Enthalpies of Formation
- Enthalpy of Reaction from Enthalpies of Formation
- Thermochemistry Practice Problems
