In the previous post that a calorimeter is a device for measuring the heat flow, and for reactions under constant pressure, the calorimeter measures the enthalpy of the reaction (ΔH).

Now, a bomb calorimeter is an equipment that measures ΔE for combustion reactions. This can be seen in the equation of internal energy change:

 

ΔE = q + w

 

w = PΔV and ΔV is zero when the volume is constant. So, for a constant volume, ΔE = q, and therefore, the bomb calorimeter measures the energy change of a chemical reaction.

 

 

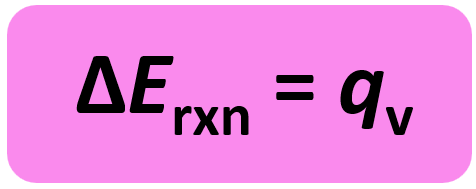
The experiment is carried out in an insulated sealed vessel called a bomb which is designed to withstand high pressures. The bomb is placed in a water container and by measuring its temperature change caused by the reaction, we determine the heat of the calorimeter.

 

 

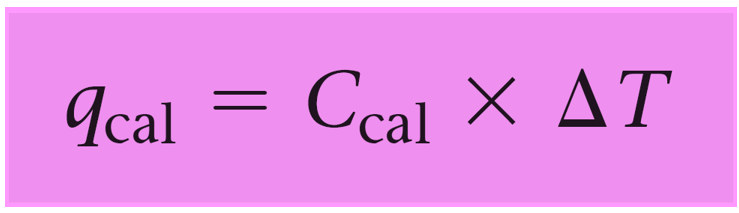
The heat capacity of the calorimeter is determined experimentally and is already known when measuring the energy change of a reaction.

Remember, because, it is a closed system, there is no heat loss, the heat released by the reaction is equal to the heat absorbed by the calorimeter q_rxn = – q_cal. This means once we calculate the q_cal, we only need to change its sign to know the heat of the reaction.

 

For example,

Calculate the energy of combustion for one mole of butane if burning a 0.367 g sample of butane (C₄H₁₀) has increased the temperature of a bomb calorimeter by 7.73 °C. The heat capacity of the bomb calorimeter is 2.36 kJ/ °C.

2C₄H₁₀(g) + 13O₂(g) → 8CO₂(g) + 10H₂O(g)

Solution

Because the combustion of butane increased the temperature of a bomb calorimeter, it is an exothermic reaction. This means, the heat goes from the reaction to the calorimeter and assuming there is no heat loss, the heat released by the reaction is equal to the heat absorbed by the calorimeter:

-q_reaction  = q_cal

 

Since the reaction occurs under conditions of constant volume, q_rxn = ΔE_rxn, so we need to calculate the q_cal using the following formula:

 

q_cal = C_cal x ΔT

 

\[{q_{{\rm{cal}}}}\; = \;{\rm{2}}{\rm{.36}}\;\frac{{{\rm{kJ}}}}{{\,\cancel{{^{\rm{o}}{\rm{C}}}}}}\,{\rm{ \times 7}}{\rm{.73}}\,\cancel{{^{\rm{o}}{\rm{C}}}}\;{\rm{ = }}\;{\rm{18}}{\rm{.2}}\,{\rm{kJ}}\]

 

Therefore, q_rxn = -18.2 kJ. However, this is not the final answer, because it is the change in the internal energy of the reaction for that specific amount of butane that was burned.

To get ΔE_rxn per mole of butane, we need to divide q_rxn by the number of moles that actually reacted. To find the number of moles, we use the mas and molar mass of butane:

 

\[{\rm{n}}\left( {{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}} \right){\rm{  =  0}}{\rm{.367 }}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{58}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.00633}}\;{\rm{mol}}\]

 

And after this, we divide the heat of the reaction by the number of moles of butane, to get the heat of the reaction per mole of butane:

 

ΔE_rxn = 18.2 kJ/0.00633 mol = 2.88 x 10³ kJ/mol

 

Alternatively, we can set up a cross-multiplication correlation reading as, 0.00633 mol C₄H₁₀  releases 18.2 kJ heat, and 1 mol will release X kJ heat:

 

0.00633 mol C₄H₁₀ – 18.2 kJ

1 mol C₄H₁₀ – X kJ

________________________________

18.2 = 0.00633 X

X = 18.2 / 0.00633 = 2.88 x 10³ kJ/mol

 

Check Also

• Energy Related to Heat and Work
• Endothermic and Exothermic Processes
• Heat Capacity and Specific Heat
• Heat Capacity Practice Problems
• What is Enthalpy
• Constant-Pressure Calorimetry
• Stoichiometry and Enthalpy of Chemical Reactions
• Hess’s Law and Enthalpy of Reaction
• Hess’s Law Practice Problems
• Standard Enthalpies of Formation
• Enthalpy of Reaction from Enthalpies of Formation
• Thermochemistry Practice Problems