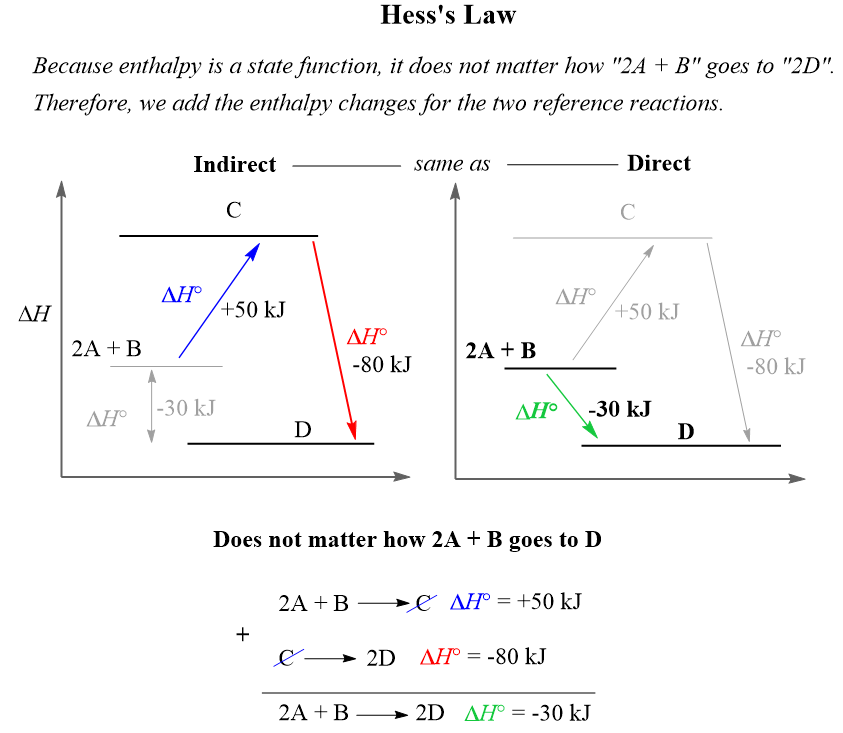
In this set of practice questions, we will summarize the main concepts of thermochemistry such as the relationship between internal energy, work and heat, exothermic and endothermic process, heat capacity, constant pressure calorimetry, constant-volume calorimetry, the enthalpy, the standard enthalpies of formation and their use in determining the heat of the reaction, and the Hess’s law.
The links to the corresponding topics are given below:
- Energy Related to Heat and Work
- Endothermic and Exothermic Processes
- Heat Capacity and Specific Heat
- Heat Capacity Practice Problems
- What is Enthalpy
- Constant-Pressure Calorimetry
- Bomb calorimeter – Constant Volume Calorimetry
- Stoichiometry and Enthalpy of Chemical Reactions
- Hess’s Law and Enthalpy of Reaction
- Hess’s Law Practice Problems
- Standard Enthalpies of Formation
- Enthalpy of Reaction from Enthalpies of Formation
Practice
What is the sign of ΔEsystem if energy flows from the surroundings into a chemical system?
A gas absorbs 62 kJ of heat and does 48 kJ of work. Calculate ΔE.
Calculate the change in internal energy of the system if it releases 415 kJ of heat and does 562 kJ of work on the surroundings.
Calculate ΔE for each of the following.
a) q = -62 kJ, w = +59 kJ
b) q = +48 kJ, w = –56 kJ
c) q = -92 kJ, w = 0 kJ
The gas in a piston is heated up by absorbing 984 J of heat and expands performing 541 J of work on the surroundings.
What is the change in internal energy for the system (the gas)?
A pump is held under 1.30 atm external pressure. How much work (in J) is required to expand its volume from 1.80 L to 3.50 L?
A balloon filled with 8.50 moles of nitrogen at 23.0 oC expands from 3.54 L to 5.64 L by increasing its temperature to 58.0 oC under constant pressure of 1.10 atm. Calculate q, w, and ΔE in kJ for the nitrogen gas in the balloon if its heat capacity is 29.15 J/°C · mol.
How much heat in kJ is required to warm 1.50 L of water from 25.0 oC to 100.0 °C? (Assume a density of 1.0 g/mL for the water.)
What is the final temperature when a 40 g sample of water at 90 °C is mixed with a 60 g sample at 25 °C?
How much heat does it take to increase the temperature of a 540.6-g sample of Fe from 20.0 °C to 84.3 °C? The specific heat of iron = 0.450 J/g °C.
Calculate the specific heat capacity of a metal if a 17.0 g sample requires 481 J to change the temperature of the metal from 25.0 °C to 67.0 °C?
Calculate the energy of combustion for one mole of butane if burning a 0.367 g sample of butane (C4H10) has increased the temperature of a bomb calorimeter by 7.73 °C. The heat capacity of the bomb calorimeter is 2.36 kJ/ °C.
How many joules of energy is required to melt 40.0 g of ice at 0 °C? The heat of fusion (ΔHfus) for ice is 334.0 J/g.
How many kJ of energy does it take to change 36.0 g of ice at -15.0 °C to water at 0. °C ? The specific heat of ice is 2.10 J/g°C and the heat of fusion (ΔHfus) for ice is 334.0 J/g. Ignore the significant figures for this problem.
The enthalpy change for the reaction is given below:
2CH3OH(l) + 3O2(g) → 4H2O(l) + 2CO2(g) ΔH = -1452.8 kJ
a) What quantity of heat is released for each mole of water formed?
b) What quantity of heat is released for each mole of oxygen reacted?
How much heat will be released if 44.8 g of SO2 is reacted with an excess of oxygen according to the following chemical equation?
2SO2(g) + O2(g) → 2SO3(g), ΔH° = –198 kJ
What is ΔH° for the following reaction
2C6H6(l) + 15O2(g) → 12CO2(g) + 6H2O(l), ΔH° = ? kJ
if the consumption of 27.3 g of benzene (C6H6) produces 1144 kJ of heat?
Based on the heat of reaction for the chlorination of methane, how much heat will be released if 233.6 grams of hydrochloric acid are formed?
CH4(g) + 3Cl2(g) → CHCl3(l) + 3HCl(g), ΔH° = -334 kJ
Calculate how many kJ of heat-energy will be released when 12.65 g of magnesium carbonate reacts with 650. mL of 0.400 M hydrochloric acid?
MgCO3(s) + 2HCl(aq) → MgCl2(aq) + H2O(l) + CO2(g), ΔH° = –112 kJ
Using the standard heats of formation given below, calculate the heat of reaction for the combustion of ammonia:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g), ΔH°rxn = ?
ΔHf° for NH3(g) = –46.2 kJ/mol
ΔHf° for NO(g) = 90.4 kJ/mol
ΔHf° for H2O(g) = –241.8 kJ/mol
Combustion of butane (C4H10) releases 5755 kJ of energy according to the following chemical equation.
2C4H10(g) + 13O2(g) → 8CO2(g) + 10H2O(l), ΔH°rxn = -5755 kJ
Calculate the molar enthalpy of formation of butane using the information given below:
ΔHf° for CO2(g) = –393.5 kJ/mol
ΔHf° for H2O(l) = –285.8 kJ/mol
Zinc is recovered from ZnS by first oxidizing it to ZnO. Calculate the enthalpy of this oxidation reaction using the data given below:
2ZnS(s) + 3O2(g) → 2ZnO(s) + 2SO2(g)
ΔHf° for SO2(g) = -296.8 kJ/mol
ΔHf° for ZnS(s) = -206.0 kJ/mol
ΔHf° for ZnO(s) = -350.5 kJ/mol
Using the standard heats of formation given below, calculate the heat of reaction between barium carbonate (BaCO3) and sulfuric acid (H2SO4).
BaCO3(s) + H2SO4(aq) → BaSO4(s) + CO2(g) + H2O(l)
ΔHf° for BaSO4(s) = -1473.2 kJ/mol
ΔHf° for CO2(g) = –393.5 kJ/mol
ΔHf° for H2O(l) = –285.8 kJ/mol
ΔHf° for BaCO3(s) = -1213.0 kJ/mol
ΔHf° for H2SO4(aq) = -814.0kJ/mol
The heat of reaction for the reaction of nitrogen oxide and chlorine is –76 kJ:
2NO(g) + Cl2(g) ⇆ 2NOCl(g)
What is the enthalpy change for the following reaction?
2NOCl(g) ⇆ 2NO(g) + Cl2(g)
The heat of reaction for the oxidation of hydrogen sulfide to sulfur dioxide accord according to the following equation is -1036 kJ:
2H2S(g) + 3O2(g) → 2SO2(g) + 2H2O(g)
What is the enthalpy change for the following reaction?
H2S(g) + 1.5O2(g) → SO2(g) + H2O(g)
Consider the thermochemical equation for the combustion of nitromethane (CH3NO2):
2CH3NO2(l) + 3/2O2(g) → 2CO2(g) + 3H2O(l) + N2(g), ΔH °rxn = -1418 kJ
What is the enthalpy change for this reaction represented by the following equation?
4CH3NO2(l) + 3O2(g) → 4CO2(g) + 6H2O(l) + N2(g), ΔH °rxn = ?
Using the Hess’s law, calculate ΔHo for the reaction:
2NO2 + Cl2(g) → 2NOCl(g) + O2(g), ΔHo = ?
Use the following reactions and given ΔH’s:
1) 2NO(g) + Cl2(g) → 2NOCl(g), ΔHo = -76 kJ
2) 2NO(g) + O2(g) → 2NO2(g), ΔHo = -114 kJ
Calculate the enthalpy for the oxidation of CO to CO2 using the enthalpy of reaction for the combustion of C to CO (ΔH = -221.0 kJ) and the enthalpy for the combustion of C to CO2 (ΔH = -393.5 kJ).
2CO(g) + O2(g) → 2CO2(g) ΔH = ?
1) C(s) + O2(g) → CO2(g) ΔH = -393.5 kJ
2) 2C(s) + O2(g) → 2CO(g) ΔH = -221.0 kJ
Calculate the enthalpy for the combustion reaction of sulfur to sulfur trioxide using the enthalpies of the two reactions shown below:
2S(s) + 3O2(g) → 2SO3(g) ΔH = ?
1) S(s) + O2(g) → SO2(g) ΔH = -297 kJ
2) 2SO3(g) → 2SO2(g) + O2(g) ΔH = 198 kJ
Using the Hess’s law, calculate ΔHo for the combustion reaction of butene:
C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(l), ΔHo = ?
Use the following reactions and given ΔH’s:
1) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ
2) C4H8(g) + H2(g) → C4H10(g), ΔHo = -126 kJ
3) 2C4H10(g) + 13O2(g) → 8CO2(g) + 10H2O(l), ΔHo = -5754 kJ
Using the Hess’s law and the enthalpies of the three combustion reactions below, calculate the enthalpy of the reaction producing methanol (CH3OH) from carbon monoxide and hydrogen gas.
CO(g) + 2H2(g) → CH3OH(g), ΔH = ?
1) 2CO(g) + O2(g) → 2CO2(g), ΔH = -566 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ
3) 2CH3OH(g) + 3O2(g) → 2CO2(g) + 4H2O(g), ΔHo = −1430 kJ
Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the combustion reaction of CH3Cl:
CH3Cl(g) + O2(g) → CO(g) + HCl(g) + H2O(l), ΔH = ?
1) CO(g) + 2H2(g) → CH3OH(g), ΔHo = -139 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ
3) CH3OH(g) + HCl(aq) → CH3Cl(g) + H2O(l), ΔHo = -28 kJ
Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the following oxidation reaction of ammonia:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g), ΔH = ?
1) N2(g) + 3H2(g) → 2NH3(g), ΔH = -92 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔH = -484 kJ
3) N2(g) + O2(g) → 2NO(g), ΔH = 181 kJ
Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the following oxidation reaction between CuO and HCl:
2CuO(s) + 4HCl(g) → 2CuCl(s) + Cl2(g) + 2H2O(g), ΔH = ?
1) CuO(s) + H2(g) → Cu(s) + H2O(g), ΔH = -85 kJ
2) 2Cu(s) + Cl2(g) → 2CuCl(s), ΔH = -274 kJ
3) H2(g) + Cl2(g) → 2HCl(g), ΔH = -184 kJ