In the previous post, we talked about the Hess’s law and how it can be used for measuring the enthalpy change (ΔH) for a reaction without making calorimetric measurements.
In short, the Hess’s law is based on the fact that enthalpy is a state function, and therefore, ΔHrxn is the same whether the reaction takes place in one step or in a series of steps.
For example, the enthalpy change for the reaction 2A + B → 2D can be calculated using the enthalpies of the two reference reactions:
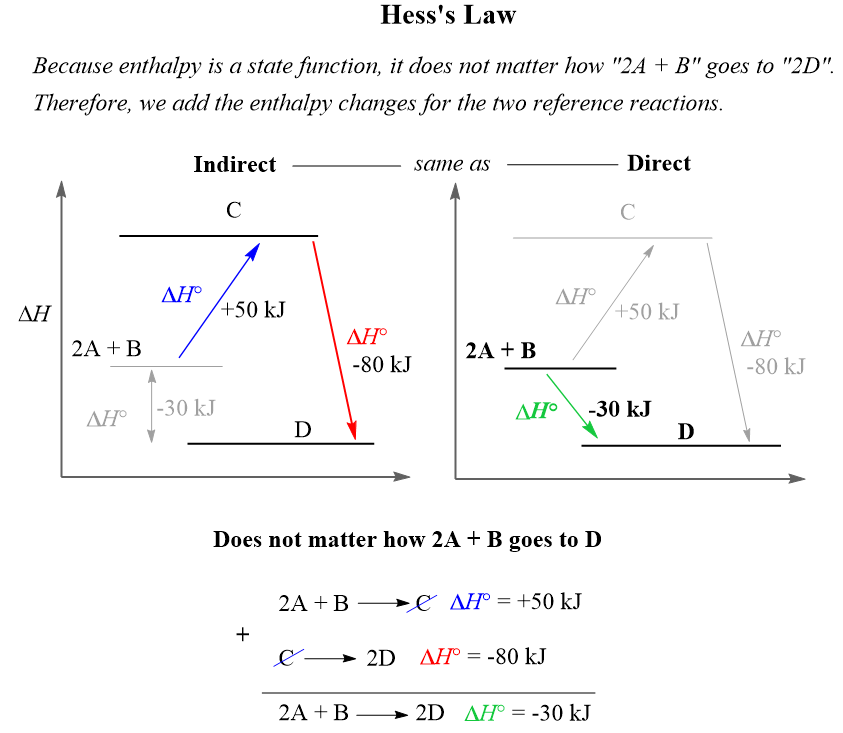
When solving a Hess’s law problem, remember your objective is to manipulate the reference equations such that when you add them up, the target equation is obtained.
Follow these two rules when changing the reference equations:
- If the equation is multiplied by any factor, the ΔH must be multiplied by the same factor.
- If the equation is reversed, the sign of ΔH must be changed.
1.
Calculate the enthalpy for the oxidation of CO to CO2 using the enthalpy of reaction for the combustion of C to CO (ΔH = -221.0 kJ) and the enthalpy for the combustion of C to CO2 (ΔH = -393.5 kJ).
2CO(g) + O2(g) → 2CO2(g) ΔH = ?
C(s) + O2(g) → CO2(g) ΔH = -393.5 kJ
2C(s) + O2(g) → 2CO(g) ΔH = -221.0 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
2.
Calculate the enthalpy for the combustion reaction of sulfur to sulfur trioxide using the enthalpies of the two reactions shown below:
2S(s) + 3O2(g) → 2SO3(g) ΔH = ?
S(s) + O2(g) → SO2(g) ΔH = -297 kJ
2SO3(g) → 2SO2(g) + O2(g) ΔH = 198 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
3.
Using the Hess’s law, calculate ΔHo for the combustion reaction of butene:
C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(l), ΔHo = ?
Use the following reactions and given ΔH’s:
1) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ
2) C4H8(g) + H2(g) → C4H10(g), ΔHo = -126 kJ
3) 2C4H10(g) + 13O2(g) → 8CO2(g) + 10H2O(l), ΔHo = -5754 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
4.
Using the Hess’s law and the enthalpies of the three combustion reactions below, calculate the enthalpy of the reaction producing methanol (CH3OH) from carbon monoxide and hydrogen gas.
CO(g) + 2H2(g) → CH3OH(g), ΔH = ?
1) 2CO(g) + O2(g) → 2CO2(g), ΔH = -566 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ
3) 2CH3OH(g) + 3O2(g) → 2CO2(g) + 4H2O(g), ΔHo = −1430 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
5.
Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the combustion reaction of CH3Cl:
CH3Cl(g) + O2(g) → CO(g) + HCl(g) + H2O(l), ΔH = ?
1) CO(g) + 2H2(g) → CH3OH(g), ΔHo = -139 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔHo = -571 kJ
3) CH3OH(g) + HCl(aq) → CH3Cl(g) + H2O(l), ΔHo = -28 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
6.
Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the following oxidation reaction of ammonia:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g), ΔH = ?
1) N2(g) + 3H2(g) → 2NH3(g), ΔH = -92 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔH = -484 kJ
3) N2(g) + O2(g) → 2NO(g), ΔH = 181 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
7.
Using the Hess’s law and the enthalpies of the given reactions, calculate the enthalpy of the following oxidation reaction between CuO and HCl:
2CuO(s) + 4HCl(g) → 2CuCl(s) + Cl2(g) + 2H2O(g), ΔH = ?
1) CuO(s) + H2(g) → Cu(s) + H2O(g), ΔH = -85 kJ
2) 2Cu(s) + Cl2(g) → 2CuCl(s), ΔH = -274 kJ
3) H2(g) + Cl2(g) → 2HCl(g), ΔH = -184 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
8.
Determine the enthalpy of formation of methane using the following data obtained from bomb calorimetry:
C(graphite) + 2H2(g) → CH4(g) ΔH °f = ?
____________________________________________
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l), ΔH ° = -891 kJ
C(s) + O2(g) → CO2(g) ΔH = -393 kJ
2H2(g) + O2(g) → 2H2O(l) ΔH = -572 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.

