When discussing the principles of electrolysis, we have seen that reduction of metal cations takes place on the cathode, and as a result, there is an accumulation of that metal. This feature of electrolysis is used in electroplating which is the coating of one metal onto another one which is used as the cathode of the electrolytic cell. For example, we can set up an electrolytic cell to plate Cr metal via electrolysis of Cr2(SO4)3:
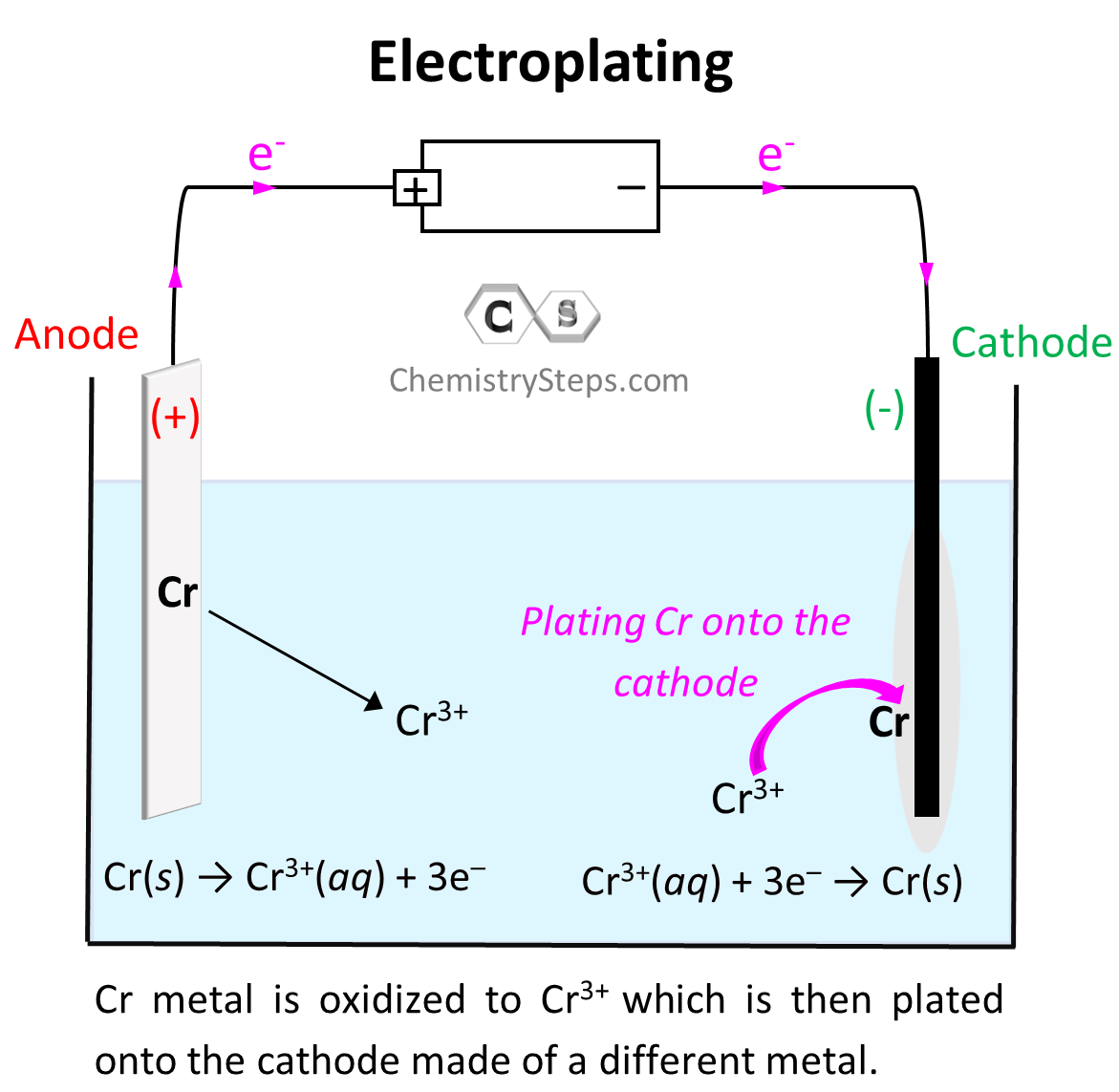
Electroplating is used for example when coating inexpensive metals with gold to prepare beautiful but more affordable jewelries.
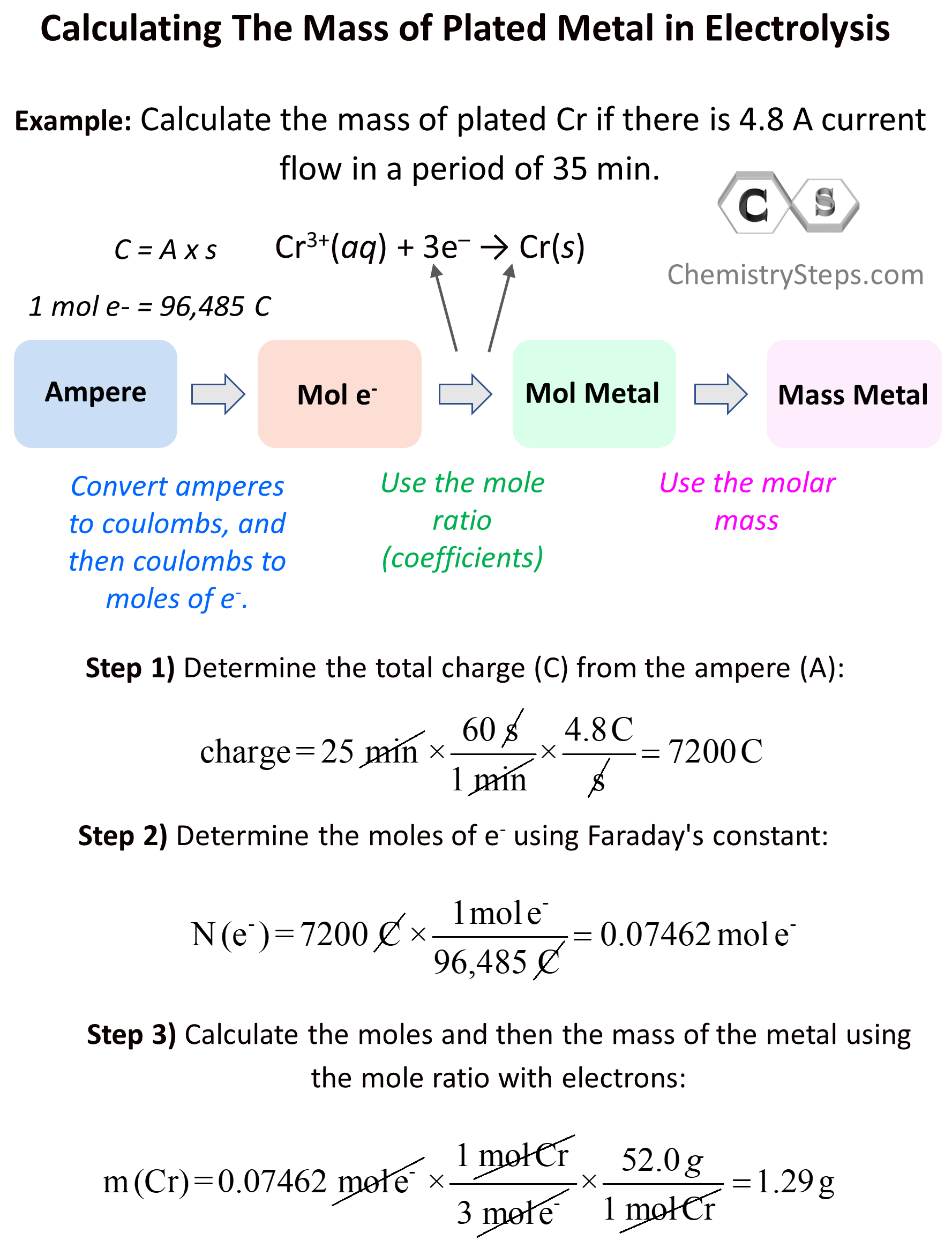
Sometimes, aside from the qualitative aspects of electrolysis, you may need to address the quantities of the species. Let’s say the question states that there is 4.8 A current flow in a period of 35 min and we need to calculate the mass of plated Cr.
The first thing we will need is the half-reaction for the formation of that metal. In this case, we have Cr, and the half-reaction can be written as:
Cr3+(aq) + 3e– → Cr(s)
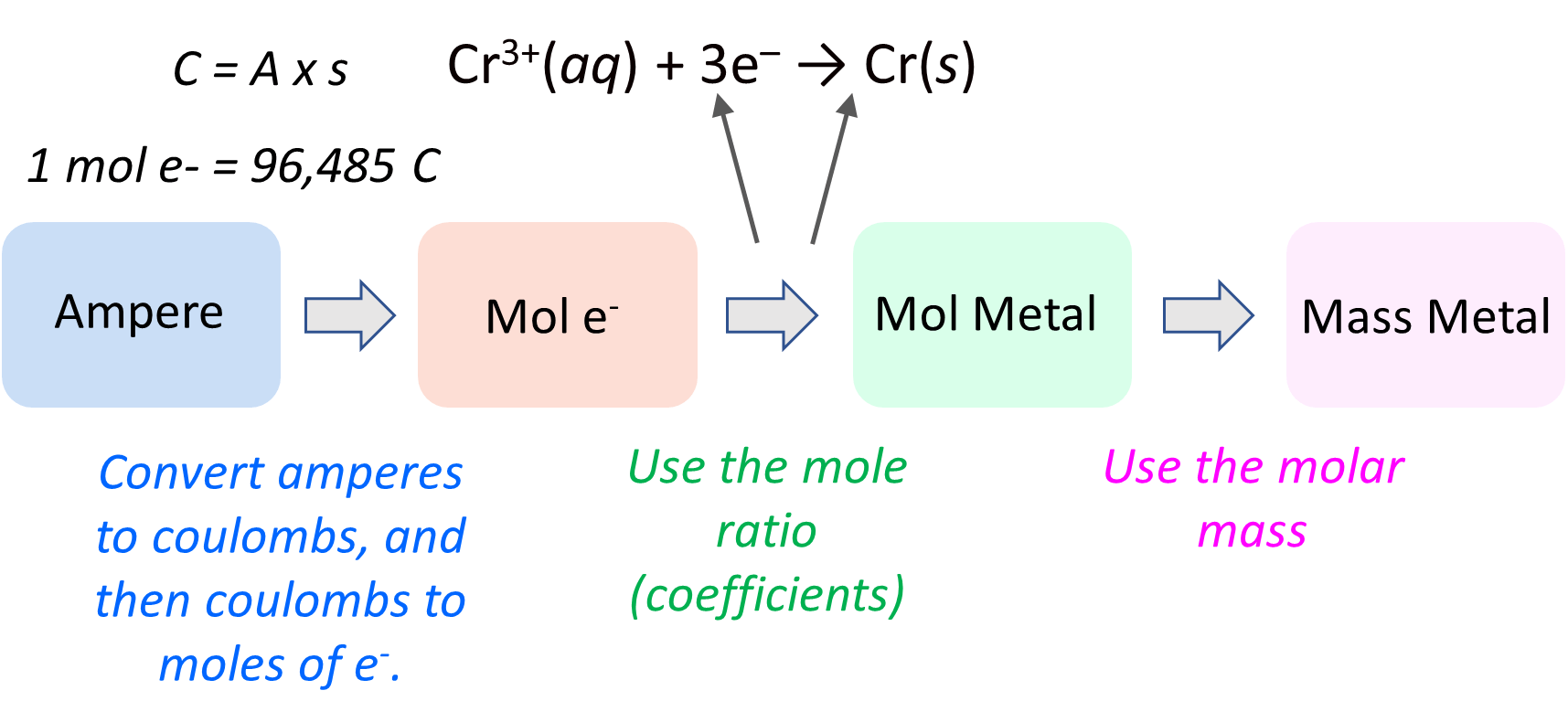
Now, how can we calculate the mass of the metal accumulated during the electrolysis? The overall plan is the following:

Let’s now break this down. The first link in the whole process is the mole ratio of the electrons and the metal. Here, we can see that there is one mole of Cr for every three moles of electrons:
3 mol e– : 1 mol Cr(s)
This means if we find the moles of the electrons, we can simply use the stoichiometric ratio with the Cr to determine its moles, and finally convert the moles to the mass of the metal. These should be pretty straightforward at this point of the semester, but if you need some refreshing of these concepts, feel free to check the linked articles.
We can also represent the half-reaction by including the moles and mass of the metal for better visualization:
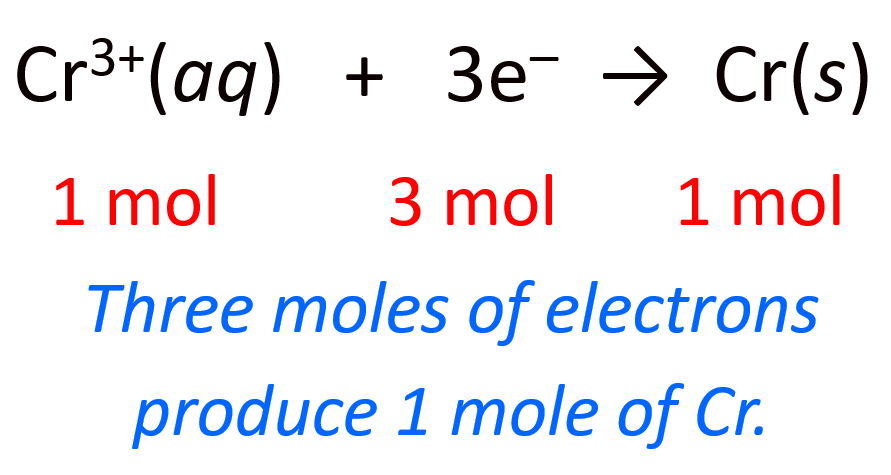
Okay, so we know that the first part of the plan is to determine the moles of the electrons. But how can we do that? The link is this part is the correlation between the A (amperes), Coulombs (C), and the moles of electrons which we can calculate based on the Faraday’s constant. Some reminders on these quantities:
Ampere (A) measures the current that passes through an electrolytic cell in a given period of time. A – how may Coulombs per second: A = C/s
Coulomb is the total electrical charge that passes through the cell. One coulomb is the magnitude of the charge delivered by a current of one ampere flowing for one second: 1C = 1A x 1s.
And Faraday’s constant (F) is the charge of 1 mole of electrons (F = 9.6485 × 104 C/mol e−).
This will be a more detailed action plan for calculating the mass of the metal:
Now, first, we need to be able to switch from A to Coulombs using this formula: 1C = 1A x 1s
Charge (C) = Current (A) x Time (s)
1C = 1A x 1s
So, let’s calculate how many coulombs per second is 4.8 A:
\[{\rm{charge}}\,{\rm{ = }}\,{\rm{25}}\,\cancel{{{\rm{min}}}}\,{\rm{ \times }}\,\frac{{{\rm{60}}\,\cancel{{\rm{s}}}}}{{{\rm{1}}\,\cancel{{{\rm{min}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{4}}{\rm{.8}}\,{\rm{C}}}}{{\cancel{{\rm{s}}}}}\, = \;7200\,{\rm{C}}\]
Now that we have the coulombs, we can use its relationship with the Faraday’s constant to calculate the mole of the electrons (F = 9.6485 × 104 C/mol e−):
\[{\rm{N}}\,{\rm{(}}{{\rm{e}}^{\rm{ – }}}{\rm{)}}\,{\rm{ = }}\,7200\,\cancel{{\rm{C}}}\,{\rm{ \times }}\,\frac{{\,{\rm{1}}\,{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}{{{\rm{96,485}}\,\cancel{{\rm{C}}}}}\, = \;0.07462\,{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}\]
Note: the answer should have two significant figures, but we won’t round off till the final answer.
Once we have the moles of electrons, we get to the easier part which is calculating the moles, and subsequently the mass of the metal. The molar mass of Cr is 52.0 g/mol, therefore, we can write that:
\[{\rm{m}}\,{\rm{(Cr)}}\,{\rm{ = }}\,0.07462\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}\,{\rm{ \times }}\,\frac{{\,{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{Cr}}}}}}{{{\rm{3}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}}}\,{\rm{ \times }}\,\frac{{52.0\,g}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{Cr}}}}}} = \;1.29\,{\rm{g}}\]
We can also show the entire calculation in a one dimensional analysis equation:
\[{\rm{m}}\,{\rm{(Cr)}}\,{\rm{ = }}\,{\rm{25}}\,\cancel{{{\rm{min}}}}\,{\rm{ \times }}\,\frac{{{\rm{60}}\,\cancel{{\rm{s}}}}}{{{\rm{1}}\,\cancel{{{\rm{min}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{4}}{\rm{.8}}\,\cancel{{\rm{C}}}}}{{\cancel{{\rm{s}}}}}\,{\rm{ \times }}\,\frac{{\,{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}}}{{{\rm{96,485}}\,\cancel{{\rm{C}}}}}\,{\rm{ \times }}\,\frac{{\,{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{Cr}}}}}}{{{\rm{3}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}}}\,{\rm{ \times }}\,\frac{{52.0\,g}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{Cr}}}}}} = \;1.29\,{\rm{g}}\]
So, there will be 1.29 g of Cr metal plated on the cathode if a current of 4.8 A is passed through the cell for 25 min.
Let’s also put together a summary for calculating the mass of a metal produced during electrolysis:
Nonmetals and Stoichiometry of Electrolysis
The stoichiometry of electrolysis is not restricted to metals only can be used for calculating the mass of any product. For example, it can be used to determine how much Cl2 is produced during the electrolysis of NaCl or how much time will be needed to produce a certain volume of the gas given the current flow.
For example: how many minutes will it take to produce 4.60 g of Cl2(g) by electrolysis of aqueous NaCl using a power supply with a current of 13 A?
Solution: The half-reaction for the formation of Cl2 from the electrolysis of NaCl is written as:
2 Cl–(aq) → Cl2(g) + 2 e–
This shows the mole ratio of Cl2 and electrons, therefore, we can calculate the moles of Cl2 to determine the moles of electrons:
\[{\rm{n}}\,{\rm{(}}{{\rm{e}}^{\rm{ – }}}{\rm{)}}\,{\rm{ = }}\,{\rm{4}}{\rm{.60}}\,\cancel{{{\rm{g}}\,{\rm{C}}{{\rm{l}}_{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}}{{{\rm{71}}\,\cancel{{{\rm{g}}\,{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{2}}\,{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.12957}}\,{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}\]
Next, we can determine the total charge (Coulombs) using the correlation of Faraday’s constant:
\[{\rm{Charge}}\,{\rm{ = }}\,{\rm{0}}{\rm{.12957}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}\,}}{\rm{ \times }}\,\frac{{\,{\rm{96,485}}\,{\rm{C}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}}}\,{\rm{ = }}\;{\rm{12,502}}\,{\rm{C}}\]
The last step is to determine the time from the charge using the correlation A = C/s. Amperes show how many Coulombs pass in 1 s, so in this case, there are 13 C passing in 1 second. Therefore, the conversion factor would be 1s/13 C:
\[{\rm{T}}\,{\rm{ = }}\,{\rm{12,502}}\,\cancel{{\rm{C}}}\;{\rm{ \times }}\,\frac{{\,{\rm{1 s}}}}{{{\rm{13}}\,\cancel{{\rm{C}}}}}\,{\rm{ = }}\;{\rm{961}}{\rm{.7}}\,{\rm{s }} \approx {\rm{ 16}}\,{\rm{min}}\]
Check Also
- Balancing Redox Reactions
- Galvanic Cells
- How to Calculate Standard Cell Potential
- The Correlation Between Eocell, ΔG°, and K
- Nernst Equation
- Nernst Equation Practice Problems
- Concentration Cells
- Electrolytic Cells
- Electrolysis
- Electrolysis of Water
- Cell Potential Practice Problems
- Eo, ΔGo, K – Practice Problems
- Electrochemistry Practice Problems
Practice
Determine the mass of metal that plates out when a solution of Cr2(SO4)3 is electrolyzed by passing 85.0 A of current for 16.5 min.
How many grams of nickel can be deposited by the passage of a constant current of 45.0 A through a Ni(NO3)2 solution for 50.0 min?
An electrolysis of a AgNO3 solution was performed by passing 135 A of current for 1.50 hours. What mass of silver plates out?
How long would it take to deposit 15.0 g copper metal by electrolysis of CuCl2 solution in a cell running with a current of 45 A?
How many grams of Cl2 gas can be produced by electrolysis of molten NaCl using a cell running 65.0 A for 2 hours?
