In the previous post, we talked about the Nernst equation which is used to calculate the cell potential under nonstandard conditions based on Eocell and the log of the reaction quotient.
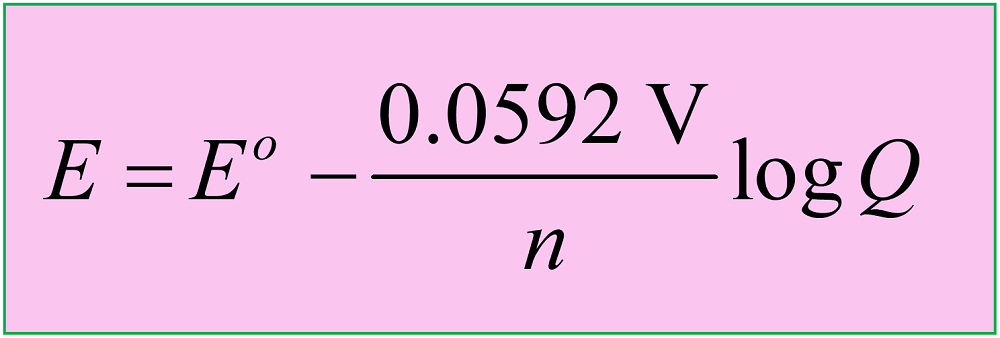
where Eo is the cell potential under standard conditions, n is the moles of the electrons in the half-reactions, and Q is the reaction quotient
Another version of the equation is when the natural logarithm of the Q is used:
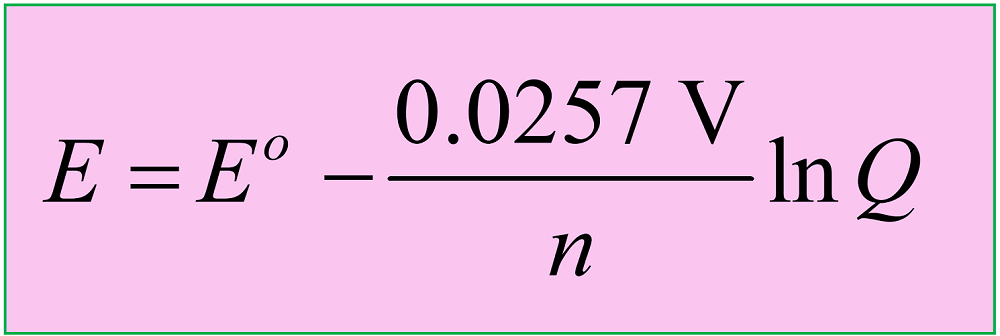
Keep in mind that both equations are applicable to reactions carried out at 25 oC (298 K).
Notice also that the cell potential under nonstandard conditions differs from the one under standard conditions, only based on the quotient.
Remember, Q has the same expression as the equilibrium constant and the only difference is that we use the given concentrations rather than the ones at the equilibrium:

Reaction quotient, Q tells us whether the forward or reverse reactions are going to be favorable based on the given concentrations of the reactants and products. The driving force here is that the system always tries to reach an equilibrium where Q becomes equal to the K:
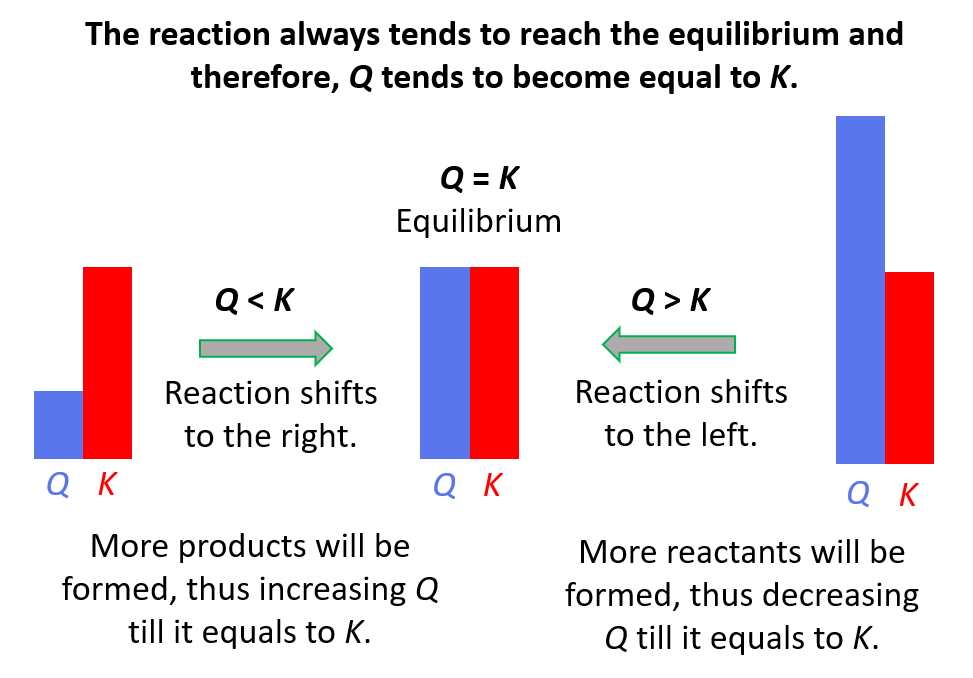
Feel free to review the concept of reaction quotient and equilibrium constant by clicking on the highlighted sections, but here is the summary of what we need to know about Q and the direction of the equilibrium:
- Q < K Reaction tends to form more products.
- Q > K Reaction tends to form more reactants.
- Q = K Reaction is already at equilibrium.
Applying this to the Nernst equation, we can write the following correlations between the cell potential and the reaction quotient:
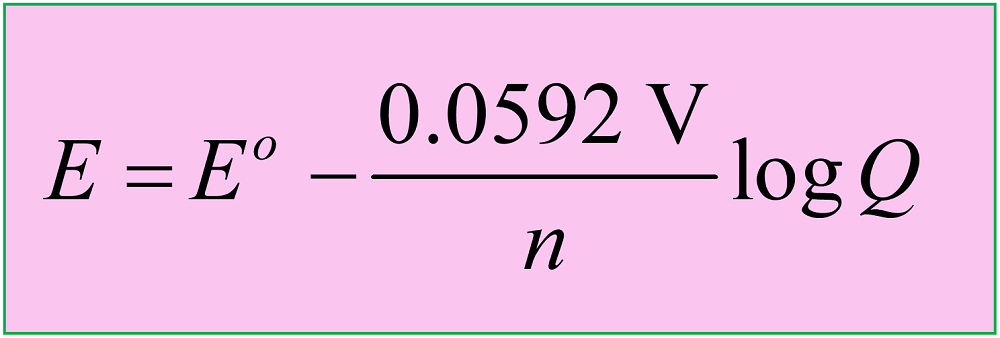
- When Q < 1, it means [reactant] > [product], ln Q < 0, so Ecell > E°cell.
- When Q = 1, it means [reactant] = [product], ln Q = 0, so Ecell = E°cell.
- When Q > 1, it means [reactant] < [product], ln Q > 0, so Ecell < E°cell.
- When Q = K, it means [product] >> [reactant], ln Q = E°cell, so Ecell = 0 .
Remember, we do not include the liquids and solids, even when they are the electrodes, in the expression for Q as it only contains those species with concentrations (and/or pressures) that can change during the reaction.
For example, in the reaction between manganese and lead ion, the Mn and Pb electrodes do not appear in the expression for Q:
Mn(s) + Pb2+(aq) → Mn2+(aq) + Pb(s)
\[E\; = \,{E^o}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[M}}{{\rm{n}}^{{\rm{2 + }}}}{\rm{]}}}}{{{\rm{[P}}{{\rm{b}}^{{\rm{2 + }}}}{\rm{]}}}}\]
Nernst Equation – Example
A voltaic cell runs the following redox reaction:
Sn2+(aq) + Mg(s) → Sn(s) + Mg2+(aq)
a) For each concentration set, determine, without using the Nernst equation, whether Ecell is larger or smaller than E°cell and b) Calculate the Ecell:
1) when [Sn2+] = 1.0 Mand [Mg2+] = 2.5 M
2) when [Sn2+] = 3.0 Mand [Mg2+] = 1.0 M
1) [Sn2+] = 1.0 Mand [Mg2+] = 2.5 M
For part (a)
To estimate if Ecell is larger or smaller than Eocell, we need to look at the reaction quotient.
The concentration of the product, Mg2+ is higher than that of Sn2+ and therefore, according to the Le Chatelier’s principle, the tendency of the forward reaction will be less than at standard conditions since Q > 1.
\[Q\, = \,\frac{{[{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}]}}{{[{\rm{S}}{{\rm{n}}^{{\rm{2 + }}}}]}}\, = \,\frac{{2.5}}{1}\, = \,2.5\]
This also means that Ecell is smaller than E°cell. Remember the pattern: if Q > 1, Ecell < E°cell, and if Q < 1, Ecell > E°cell.
Part (b). To confirm this assessment, we need to use the Nernst equation and calculate Ecell.
\[E\; = \,{E^o}\; – \,\frac{{0.0257\;{\rm{V}}}}{n}\,\ln \,Q\]
Remember, V is just a unit here, and if it confuses you, you can write the equation as:
\[E\; = \,{E^o}\; – \,\frac{{0.0257}}{n}\,\ln \,Q\]
First, calculate the E°cell by writing the half-reactions and looking up each cell potential. We have a separate post on calculating the cell potential at standard conditions so feel free to check that for more details.
Sn2+(aq) + 2e– → Sn(s) Eo = -0.14 V
Mg(s) → Mg2+(aq) + 2e– Eo = +2.37 V
Eocell = -0.14 V + 2.37 V = 2.23 V
And know, we can plug the numbers into the Nernst equation and determine the Ecell:
\[E\; = \,{E^o}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[M}}{{\rm{g}}^{{\rm{2 + }}}}{\rm{]}}}}{{{\rm{[S}}{{\rm{n}}^{{\rm{2 + }}}}{\rm{]}}}}\]
\[E\; = \,2.23\,{\rm{V}}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[2}}{\rm{.5]}}}}{{{\rm{[1}}{\rm{.0]}}}}\; = \;2.218\,{\rm{V}}\]
Because Q = 2.5, the difference between Ecell and E°cell is not very large due to the logarithm. So, at this concentration ratio, the cell potential is smaller than E°cell, however, the reaction is still spontaneous and will proceed forward until an equilibrium is reached when Q = K and Ecell = 0.
2) [Sn2+] = 3.0 M and [Mg2+] = 1.0 M
Part (a)
There is more reactant than product in the system, so the reaction will tend to shift forward more than it would under standard conditions. Therefore, Ecell should be larger than E°cell: Q < 1, Ecell > E°cell.
Part (b)
We have already determined the E°cell, so we can use it in the Nernst equation to calculate the Ecell:
\[E\; = {\mkern 1mu} {E^o}\; – {\mkern 1mu} \frac{{{\rm{0}}.{\rm{0257}}\;{\rm{V}}}}{{\rm{2}}}{\mkern 1mu} {\rm{ln}}{\mkern 1mu} \frac{{[{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}]}}{{[{\rm{S}}{{\rm{n}}^{{\rm{2 + }}}}]}}\]
\[E\; = \,2.23\,{\rm{V}}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[1]}}}}{{{\rm{[3}}{\rm{.0]}}}}\; = \;2.244\,{\rm{V}}\]
Check Also
- Balancing Redox Reactions
- Galvanic Cells
- How to Calculate Standard Cell Potential
- The Correlation Between Eocell, ΔG°, and K
- Nernst Equation
- Concentration Cells
- Electrolytic Cells
- Electrolysis
- Electrolysis of Water
- Calculating the Mass of Metal in Electroplating
- Cell Potential Practice Problems
- Eo, ΔGo, K – Practice Problems
- Electrochemistry Practice Problems
Practice
A voltaic cell runs the following redox reaction at 25 oC:
Fe2+(aq) + Mg(s) → Mg2+(aq) + Fe(s)
Determine whether Ecell is larger or smaller than E°cell and determine the Ecell for the following concentrations:
a) when [Fe2+] = 1.0 M and [Mg2+] = 2.5 M
b) when [Fe2+] = 3.0 M and [Mg2+] = 1.0 M
Calculate E°, E, and ΔG for the following cell reaction:
Mn(s) + Pb2+(aq) → Mn2+(aq) + Pb(s)
[Mn2+] = 0.164 M, [Pb2+] = 0.038 M
A galvanic cell operates on the following redox reaction:
2MnO4–(aq) + 10Br–(aq) + 16H+(aq) → 2Mn2+(aq) + 5Br2(l) + 8H2O(l)
Calculate the cell potential at 25 oC, given the concentrations of the aqueous components are: [MnO4–] = 0.0250 M, [Br–] = 0.0150 M, [Mn2+] = 0.380 M, and [H+] = 0.64 M.
A voltaic cell consists of a Mg/Mg2+ half-cell and a Sn/Sn2+ half-cell at 25 °C. The initial concentrations of Sn2+ and Mg2+ are 1.80 M and 0.250 M, respectively.
a) Calculate the initial cell potential.
b) What is the cell potential when the concentration of Sn2+ dropped to 0.650 M?
c) Determine the concentrations of Sn2+ and Mg2+ ions when the cell potential falls to 2.15 V.
A voltaic cell consists of a Zn/Zn2+ half-cell and a H2/H+ half-cell at 25 °C. Calculate the initial cell potential if [Zn2+] = 0.0250 M, [H+] = 2.80 M, P(H2) = 0.45 atm.
Determine the emf of a cell consisting of a Sn2+/Sn half-cell and a Pt/H+/H2 half-cell if [Sn2+] = 0.12 M, [H+] = 0.0650 M, and P(H2) = 1.25 atm?
