We have seen in the previous post that the cell potential depends not only on the type of the metal but also on the concentration of their electrolyte solutions. This is a cell under nonstandard conditions and its potential is calculated using the Nernst equation:

 

 

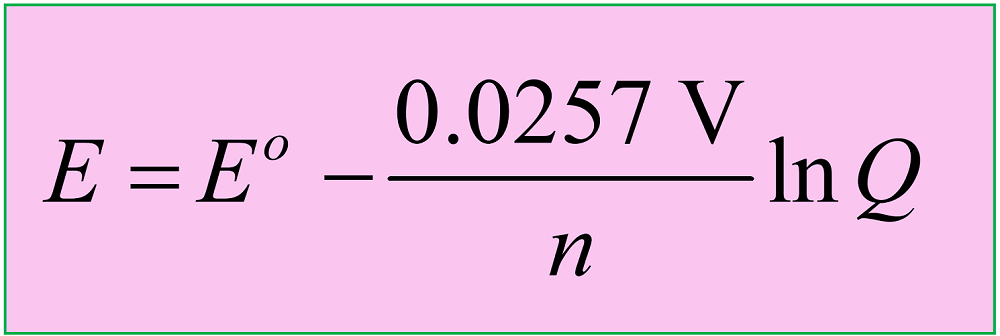
where E^o is the cell potential under standard conditions, n is the moles of the electrons in the half-reactions, and Q is the reaction quotient

 

Reaction quotient, Q tells us whether the forward or reverse reactions are going to be favorable based on the given concentrations of the reactants and products. The driving force here is that the system always tries to reach an equilibrium where Q becomes equal to K:

 

 

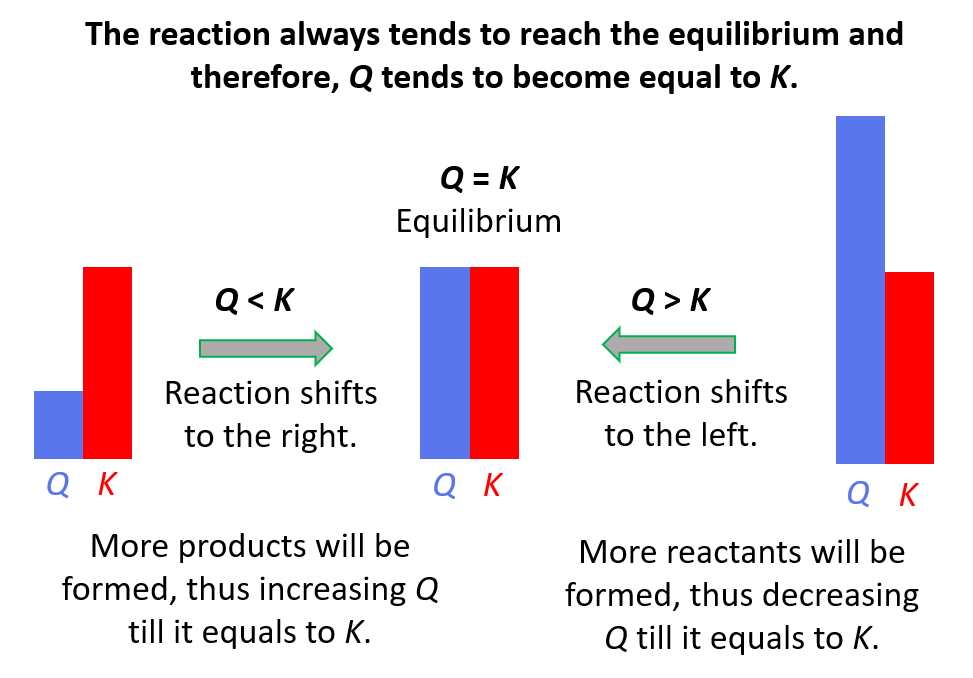
Feel free to review the concept of reaction quotient and equilibrium constant by clicking on the highlighted sections, but here is the summary of what we need to know about Q and the direction of the equilibrium:

 

• Q < K Reaction tends to form more products.
• Q > K Reaction tends to form more reactants.
• Q = K Reaction is already at equilibrium.

 

Now, here is a question: can we construct a Galvanic cell using identical electrodes for the anode and cathode and simply rely on the difference in the concentrations? And the answer is yes, even though having identical electrodes would mean the E^o_cell is zero, the E_cell will still be greater than zero because of different concentrations. 

Let’s suppose we have an electrochemical cell made of copper electrodes merged in CuSO₄ solutions of different concentrations – suppose 0.10 M and 2.0 M:

 

 

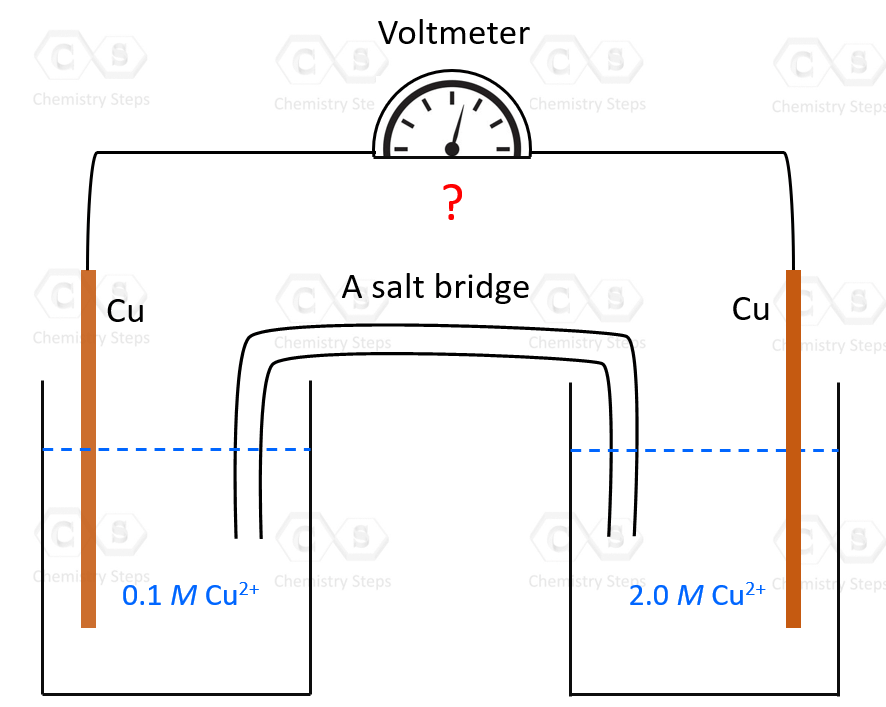
So, how can we predict which direction the electron flow is going to be? Well, first of all, how do we know that there is going to be electron flow which would only happen if there were an overall cell potential?

The answer to this question is the tendency of the system to establish an equilibrium by making the concentration of Cu²⁺ ions equal in both cells. An analogy would be mixing two solutions of CuSO₄ with different concentrations – at the end the solution will be of intermediate equal concentrations.

In the electrochemical cell, the solutions are not in immediate contact so the ions cannot mix. Instead, it is the electron flow that will balance the concentrations. The flow must be such that it reduced the Cu²⁺ concentration in the concentrated solution and thus increases it in the dilute solution:

 

 

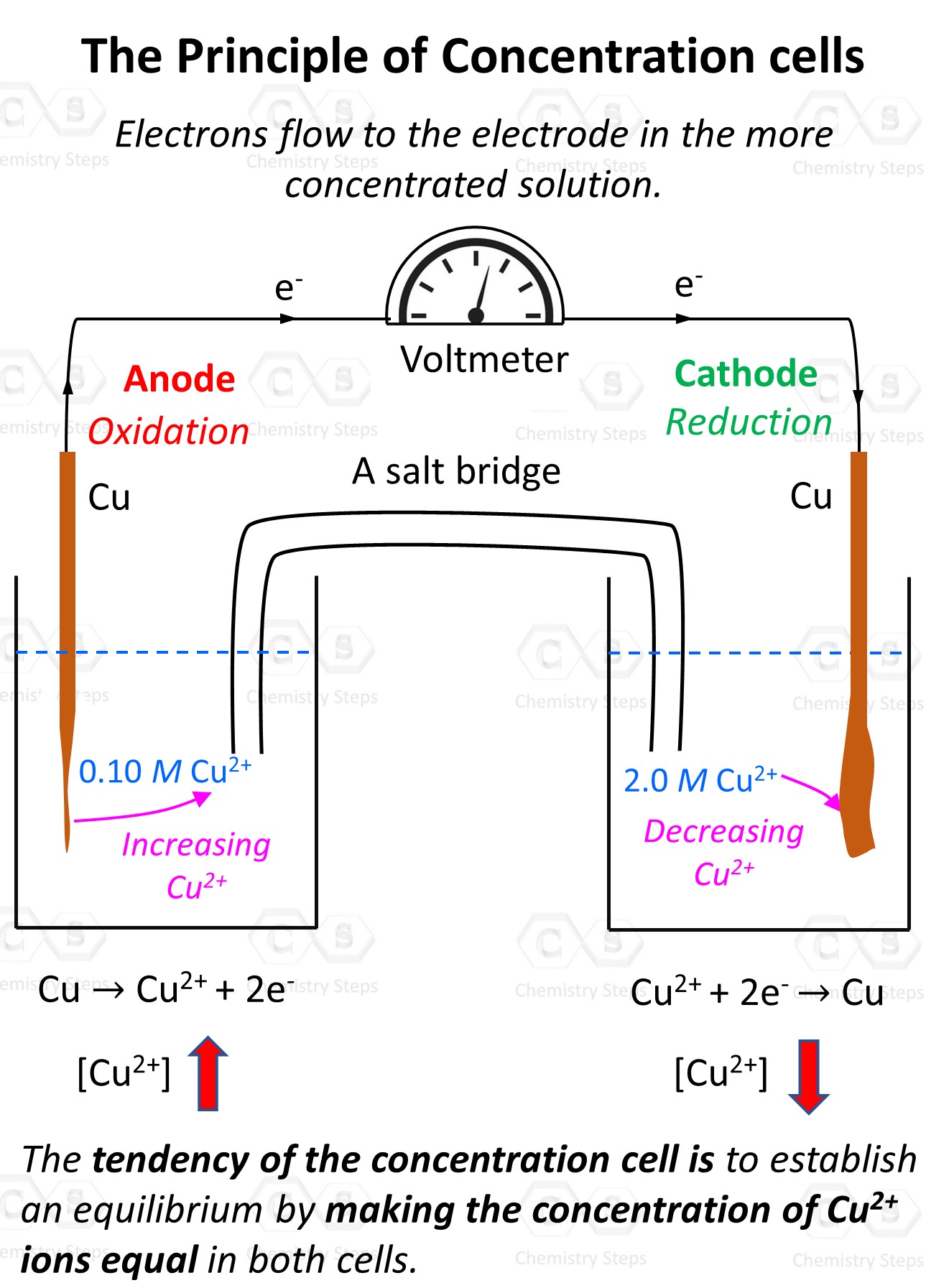
So, remember, the tendency of the electron flow is towards the concentrated solution as the electrons reduce the cation and balance the concentration in the two solutions.

Therefore, we have oxidation on the electrode in the dilute solution (anode), and the reduction occurs in the solution with the concentrated solution (cathode).

 

Calculating the Cell Potential with Different Concentrations

This is a cell under nonstandard conditions, and therefore, we are going to use the Nernst equation to calculate its potential (E_cell):

 

 

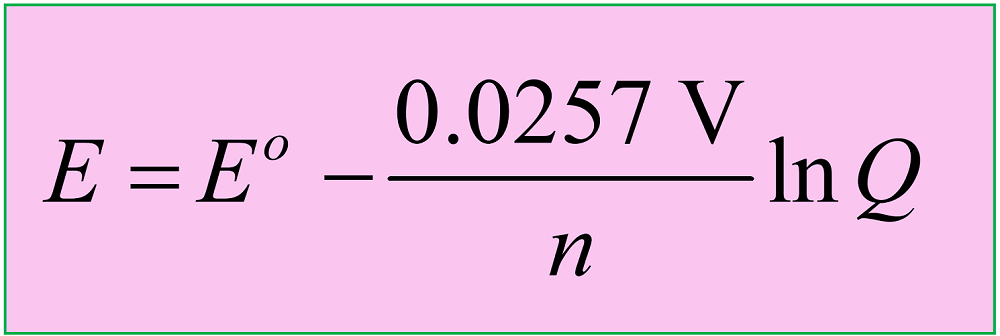
The E^o_cell is equal to zero because when the concentrations are equal in both solutions, each cell has the same potential. We can confirm this by writing the half-reactions and calculating the cell potential under standard conditions as we did before:

 

Anode: Cu(s) → Cu²⁺(1.0 M) + 2e^–   E^o = -0.34 V

Cathode: Cu²⁺(1.0 M) + 2e^–  → Cu(s)  E^o = +0.34 V

E^o_cell = -0.34 V + 0.34 V = 0 V

 

Now, the key part – how are we going to calculate the reaction quotient? For this, we need to know the reactant and product.

Remember, Q has the same expression as the equilibrium constant and the only difference is that we use the given concentrations rather than the ones at the equilibrium:

 

a A(aq) + b B(aq) → c C(aq) + d D(aq)

 

To determine the Q, let’s first write the two half-reactions here:

 

Anode (lower concentration): Cu(s) → Cu²⁺(0.10 M) + 2e^–  

Cathode (higher concentration): Cu²⁺(2.0 M) + 2e^– → Cu(s) 

Overall: Cu²⁺(2.0 M) → Cu²⁺(0.10 M) E = ?

 

Notice that we must specify the concentrations otherwise everything will be canceled like in the case of standard conditions.

And now that we know the product and reactant, we can set up the correct expression for the Q in the Nernst equation:

 

\[E\; = \,{E^o}\; – \,\frac{{0.0257\;{\rm{V}}}}{n}\,\ln \,Q\]

 

\[E\; = \,0\; – \,\frac{{0.0257\;{\rm{V}}}}{2}\,\ln \,\frac{{\left[ {{\rm{C}}{{\rm{u}}^{{\rm{2 + }}}}(0.10M)} \right]}}{{\left[ {{\rm{C}}{{\rm{u}}^{{\rm{2 + }}}}(2.0M)} \right]}}\]

 

\[E\; = \, – \,\frac{{0.0257\;{\rm{V}}}}{2}\,\ln \,\frac{{0.10}}{{2.0}}\; = \, + 0.038\,{\rm{V}}\]

 

To summarize, when asked to calculate the potential of a concentration cell, remember the electrons flow to the electrode in the more concentrated solution. Write the half-reactions based on that, make sure to specify the concentrations of the cations and cancel the repeating units (solids and electrons) to obtain the overall equation which will allow setting up the correct expression for the quotient. After this, use the Nernst equation to calculate the cell potential.

 

Check Also

• Balancing Redox Reactions
• Galvanic Cells
• How to Calculate Standard Cell Potential
• The Correlation Between E^o_cell, ΔG°, and K
• Nernst Equation
• Nernst Equation Practice Problems
• Electrolytic Cells
• Electrolysis
• Electrolysis of Water
• Calculating the Mass of Metal in Electroplating
• Cell Potential Practice Problems
• E^o, ΔG^o, K – Practice Problems
• Electrochemistry Practice Problems