Introduction to the Hybridization
Let’s start first by answering this question: Why do we need the hybridization theory?
Here is one answer to this. It is confirmed experimentally that the carbon atom in methane (CH4) and other alkanes has a tetrahedral geometry. A reminder that in tetrahedral geometry, all the angles are 109.5o and the bonds have identical lengths. Remember also that covalent bonds form as a result of orbital overlapping and sharing two electrons between the atoms. So, in order to predict the valency and geometry of the carbon atom, we are going to look at its electron configuration and orbitals.
C – 1s22s22p2
The valence electrons are the ones in the 2s and 2p orbitals and these are the ones that participate in bonding and chemical reactions.

You can see from the electron configuration that it is impossible to make four, identical in bond length, energy, and everything else (degenerate) bonds because one of the orbitals is a spherical s, and the other three are p orbitals. And this is where we get into the need of a theory that can help us explain the known geometry and valency of the carbon atom in many organic molecules. Hybridization is a theory that is used to explain certain molecular geometries that would have not been possible otherwise.
The sp3 hybridization
Now, let’s see how that happens by looking at methane, CH4 as an example. In the first step, one electron jumps from the 2s to the 2p orbital. This leads to the excited state of the carbon:

Pay attention that the electron goes uphill as the p subshell is higher in energy than the s subshell and this is not energetically favorable, but we will see how it is compensated in the next step when orbitals are mixed (hybridized).
So, in the next step, the s and p orbitals of the excited state carbon are hybridized to form four identical in size, shape, and energy orbitals.

The number of the hybrid orbitals is always the same as the number of orbitals that are mixed. So, four orbitals (one 2s + three 2p) are mixed and the result is four sp3 orbitals. These are hybrid orbitals and look somewhat like the s and p orbitals. And again, we call them sp3 because they are formed from one s orbital and three p orbitals.
The formation of these degenerate hybrid orbitals compensates for the energy uphill of the s-p transition as they have lower energy than the p orbitals.
The four sp3-hybridized orbitals arrange in a tetrahedral geometry and make bonds by overlapping with the s orbitals of four hydrogens: This explains the symmetrical geometry of methane (CH4) where all the bonds have the same length and bond angle.

All four C – H bonds in methane are single bonds that are formed by head-on (or end-on) overlapping of sp3 orbitals of the carbon and s orbital of each hydrogen.
The bonds that form by the head-on overlap of orbitals are called σ (sigma) bonds because the electron density is concentrated on the axis connecting the C and H atoms.
Ethane, CH3-CH3 and other alkanes
If instead of one hydrogen, we connect another sp3-hybridized carbon, we will get ethane:

And consequently, in all the alkanes, there is a sigma bond between the carbon atoms and the carbon-hydrogen atoms, and the carbons are sp3 hybridized with tetrahedral geometry:

To generalize this, any atom with four groups (either an atom or a lone pair) is sp3 hybridized. And the way to look at this is, in order for the four groups to be as far away from each other as possible like we learned in the VSEPR theory, the groups need to be in identical four orbitals which is only possible in the sp3 hybridization.
sp3 Hybridization with A Lone Pair(s)
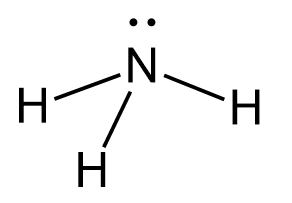
Let’s consider an example where the atom is sp3-hybridized but instead of four atoms, it has three atoms and a lone pair. A typical example is ammonia, NH3. Nitrogen is the next element after carbon, with an electron configuration of 1s22s22p3.
Now, the principle is the same as we have just seen for carbon, however, when the three p orbitals are mixed with one s orbital, four sp3 orbitals are formed where one of them is filled with two electrons:

This one hybrid orbital accommodates the lone pair of the nitrogen, while the other three overlap with the s orbitals of hydrogen thus making three sigma N-H bonds.
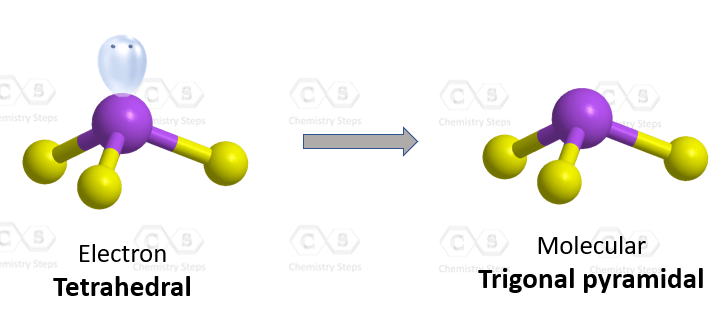
The central atom has 3 atoms and a lone pair, so the steric number is equal to 4 (SN = 4). Remember, the steric number is the sum of the atoms and lone pairs on an atom, and it dictates the hybridization and the geometry of that atom. Therefore, the electron geometry is tetrahedral while the molecular geometry is trigonal pyramidal:
A practice example: what is the hybridization of the oxygen in the following molecule?

The oxygen is connected to two atoms and has two lone pairs. In total – four groups, and that and therefore, it is sp3 hybridized. The difference with nitrogen in ammonia is that it has two lone pairs, which makes a tetrahedral electron geometry and bent molecular geometry. It is very similar to what we have water:
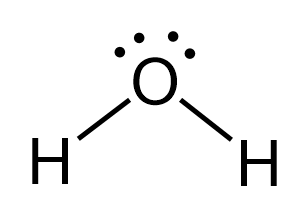
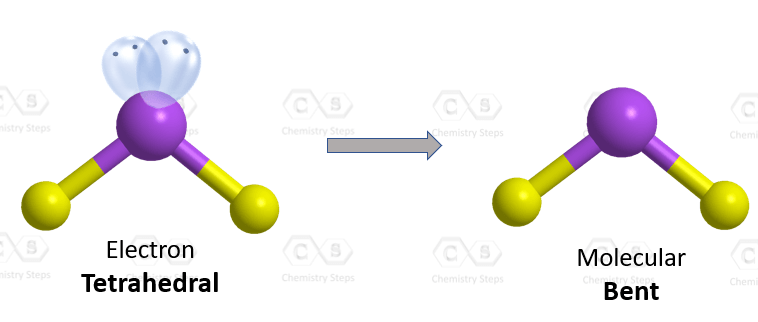
The central atom has a steric number of 4 – two atoms and two lone pairs. The electron geometry, therefore, is tetrahedral, and the molecular geometry is bent.
The sp2 hybridization
When the excited state carbon atom is formed, the sp3 hybridization is not the only option of mixing the orbitals. The sp2 hybridization occurs when the s orbital is mixed with only two p orbitals as opposed to the three p orbitals in the sp3 hybridization. So, three orbitals are mixed, and the outcome is three hybrid orbitals which are called sp2 hybrid orbitals.
For example, the central atom in BF3 is sp2 – hybridized. One s orbital of boron is mixed with two p orbitals forming thee sp2 hybrid orbital and one empty p orbital:
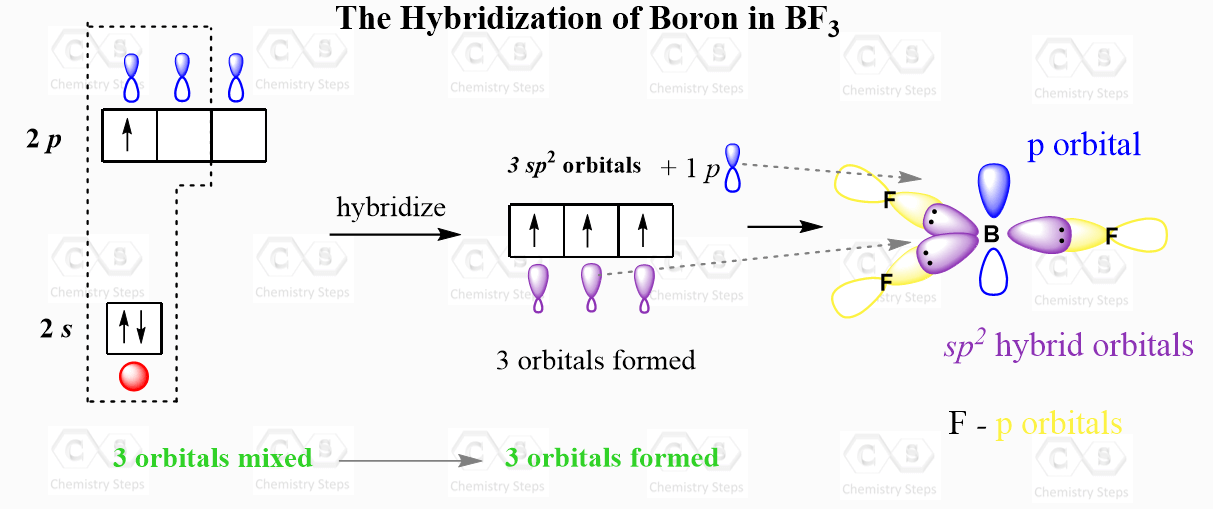
The thee sp2 orbitals overlap with the p orbitals of fluorine making three covalent bonds. There is an argument that the fluorine atoms are also hybridized, and more specifically, they are sp3-hybridized which would mean that instead of the p orbitals, they use one of the sp3 orbitals to make these bonds and the other three accommodate the lone pairs. I accept both answers from my students, so check with your instructor for their view on this.
As for the geometry, the central atom has three bonds and no lone pairs, therefore, both the electron and molecular geometries are trigonal planar. The bond angle between the fluorine atoms is 120o.

The sp2 Hybridization of Carbon Atoms
Moving a little bit towards organic molecules, we see that with the same mechanism, the carbon atom makes sp2 hybridization:

The 2s orbital is mixed with two 2p orbitals and the resulting 3 sp2 orbitals are then arranged in a trigonal planar geometry (120o). An important difference here, compared to the sp3 hybridization, is the left-out (unhybridized) p orbital that did not participate in the hybridization. This orbital is placed at 90o to the plane of the trigonal planar arrangement of the three sp2 orbitals:

Carbon hybridization in Ethylene – C2H4
Two sp2 hybridized carbon atoms can make a sigma bond by overlapping one of the three sp2 orbitals and thus bond with two hydrogens each and two hydrogens make sigma bonds with each carbon by overlapping their s orbitals with the other two sp2 orbitals.

This makes three bonds for each carbon and one p orbital left. Remember, the standard valency of carbon is four and it likes to have four bonds.
This fourth bond is formed by the side-by-side overlap of the two 2p orbitals on each carbon. This type of bonding by a side-by-side overlap of the orbitals is called a π bond.
So, the two carbons in ethylene, which is the first member of the alkene family, are double-bonded. In each double bond, there is one sigma and one π bond.

Here are some key parameters about the sp2 hybridization and double bonds that you need to know:
* All the atoms on the double bond are in one plane.
* The angle between atoms is 120o.
* The angle between the plane and p orbitals is 90o.
The sp hybridization
In sp hybridization, the s orbital of the excited state carbon is mixed with only one out of the three 2p orbitals. It is called sp hybridization because two orbitals (one s and one p) are mixed:

The resulting two sp hybrid orbitals are then arranged in a linear geometry (180o) and the two unhybridized 2p orbitals are placed at 90o:

Let’s see how this happens in acetylene- C2H2. The two carbon atoms make a sigma bond by overlapping the sp orbitals.

One hydrogen bonds to each carbon atom by overlapping its s orbital with the other sp orbital.
The two p orbitals of each carbon overlap to make two π bonds.
The key parameters of the sp hybridization and triple bond:
* All the atoms have linear geometry.
* The angle between atoms is 180o.
* In a triple bond there is one σ (sigma) and two π (pi) bonds.
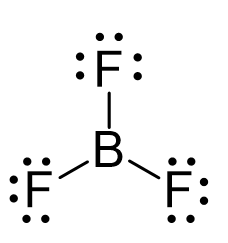
So far, we have talked about geometries that are adopted when the central atom has a steric number 1-4. That is, the sum of atoms and lone pairs on it does not exceed four. Now, for molecules with shapes trigonal bipyramidal or octahedral, the steric number is 5 and 6 respectively, and therefore, 5 or 6 orbitals are needed to make these bonds and accommodate any lone pairs. For example, PCl5 has a trigonal bipyramidal geometry and SF6 has an octahedral geometry. So, let’s start with the trigonal bipyramidal geometry which is achieved when the central atom adopts an sp3d hybridization.
The sp3d hybridization
The first thing to mention here is that the elements capable of adopting trigonal bipyramidal or octahedral geometry must be in period 3 or higher, because d orbitals are needed to produce five or more hybrid orbitals. For example, the electron configuration of phosphorous is:
P – 1s22s22p63s23p3
And in addition to the 3s and 3p orbitals, it also has the five 3d orbitals available for hybridization. Let’s draw these orbitals and see how the sp3d hybridization is achieved:

The five half-filled sp3d orbitals are formed by mixing one s (the 3s orbital), three p (the 3p orbitals), and one d (one 3d orbital). Four 3d orbitals are left unhybridized and empty. Each of the sp3d orbitals makes a bond with the p orbital of chlorine forming a trigonal bipyramidal geometry.

Even though there is a constant debate about whether the d orbitals are involved in these types of hybridizations, this answer is usually accepted in undergraduate general chemistry courses. Ultimately, it is on your professor, as they are the authority in the class.
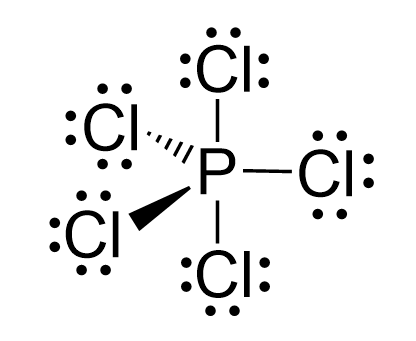
Let’s also consider the structure of BrF3 where the central atom is sp3d hybridized but only has 3 atoms connected.
The electron configuration of Br is:
Br – 1s22s22p63s23p5
Just like phosphorus, in addition to the 3s and 3p orbitals, it also has the five 3d orbitals available and one of them is involved in the sp3d hybridization:
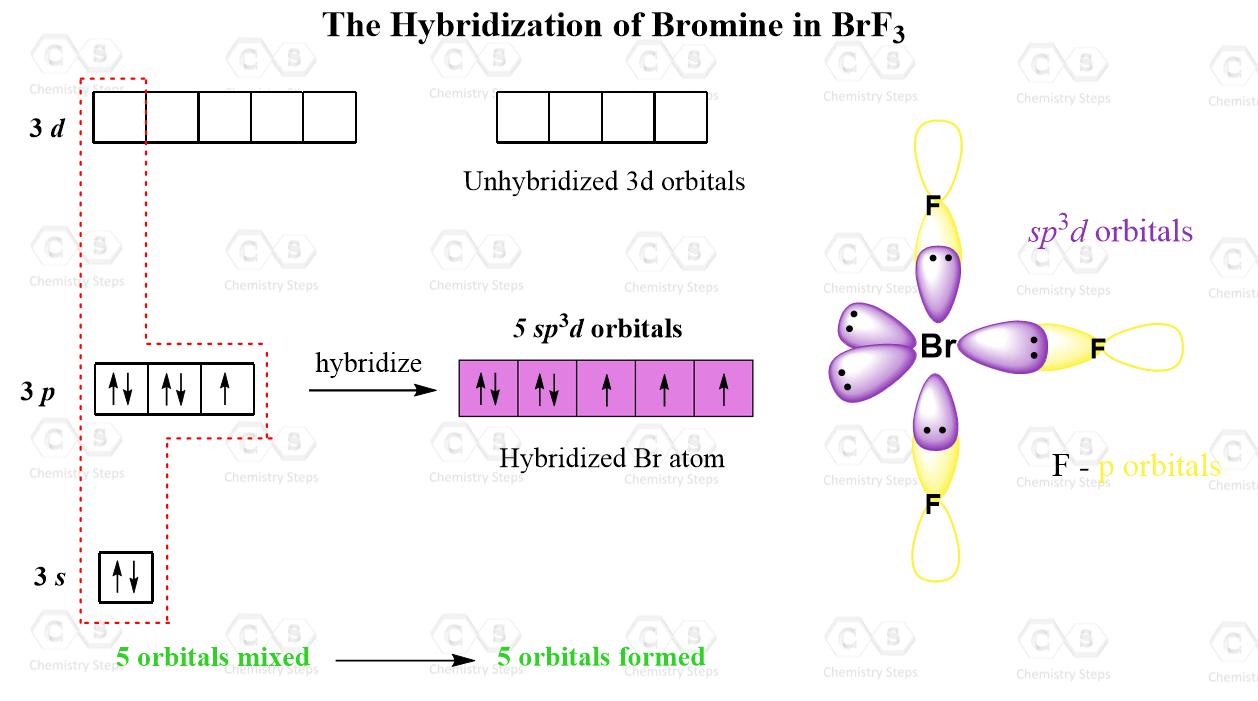
Notice that unlike the phosphorus in PCl5, only three of the five hybrid orbitals are half-filled while the two are accommodating the lone pairs.
We can also see this by drawing the Lewis structure of BrF3:
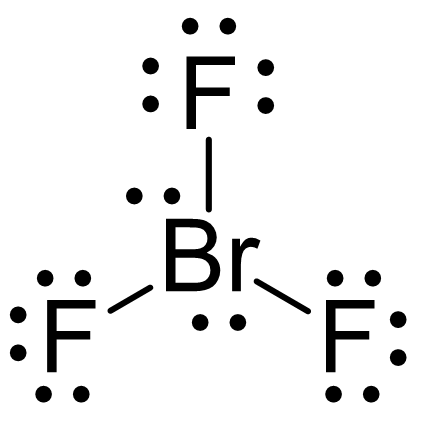
The central atom has 3 atoms and 2 lone pairs, therefore, the electron geometry is trigonal bipyramidal, while the molecular geometry is T-shaped:
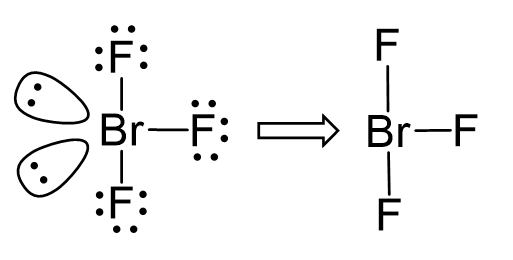
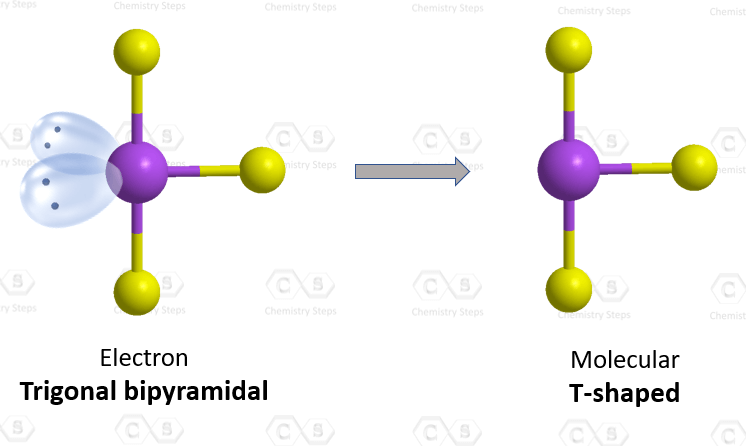
Notice that the lone pair does not go in axial positions (up or down).
The sp3d2 hybridization
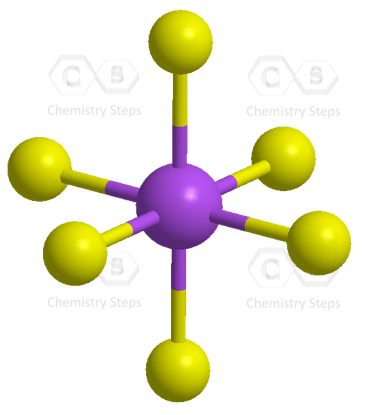
Let’s consider the structure of sulfur hexafluoride, SF6. The central atom has six atoms connected, and therefore, it needs six equivalent orbitals, which is achieved by the sp3d2 hybridization.
The electron configuration of sulfur is:
S – 1s22s22p63s23p4
You may look at it and say, it is still similar to the configuration of P and Br that adopted sp3d hybridization, so how is the sulfur going to be sp3d2 and make six bonds? And the difference is that there are two d orbitals mixed with the s and p orbitals thus making six hybrid orbitals each hosting one electron:

There are six sp3d2 half-filled orbitals of the S atom and each overlaps with a half-filled 2p orbital of an F atom.
As for the geometry, the central atom has 6 atoms connected to it, and no lone pairs, therefore, both geometries are octahedral:
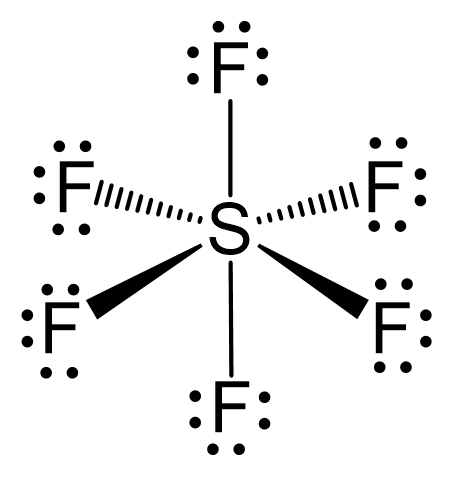
To summarize the key concepts about the hybridization of atomic orbitals, remember that the hybridization theory helps explain the geometry of molecules. The type and the shape of hybrid orbitals formed depend on the types of atomic orbitals mixed. What is true for all the hybridizations is that the number of the hybrid orbitals is always equal to the number of orbitals that are mixed.
For those of you taking organic chemistry, you will not need to deal with the hybridizations and geometries for steric number > 4 as carbon can only make four bonds at most. Check the shorter version of this article (and hundreds of other) tailored of the structure of organic molecules.
Practice
Determine the hybridization, the electron- and molecular geometry of the following molecules.
| (a) BF3 | (b) CH2O | (c) HCN | (d) BeCl2 | (e) CH2Cl2 |
| (f) SOCl2 | (g) SO2 | (h) PCl5 | (i) XeO4 | (j) NCl3 |
| (k) SiCl4 | (l) SF2 | (m) H2S | (n) SO3 | (o) COCl2 |
| (p) PCl3 | (q) OF2 | (r) BrF5 | (s) N2O | (t) SF6 |
| (u) POCl3 | (x) XeF2 | (y) XeF4 | (z) C2H2 |
For each marked atom, add any missing lone pairs of electrons to determine the steric number, electron and molecular geometry, approximate bond angles, and the hybridization state.
You can also download the questions as a PDF worksheet to print and work on here.
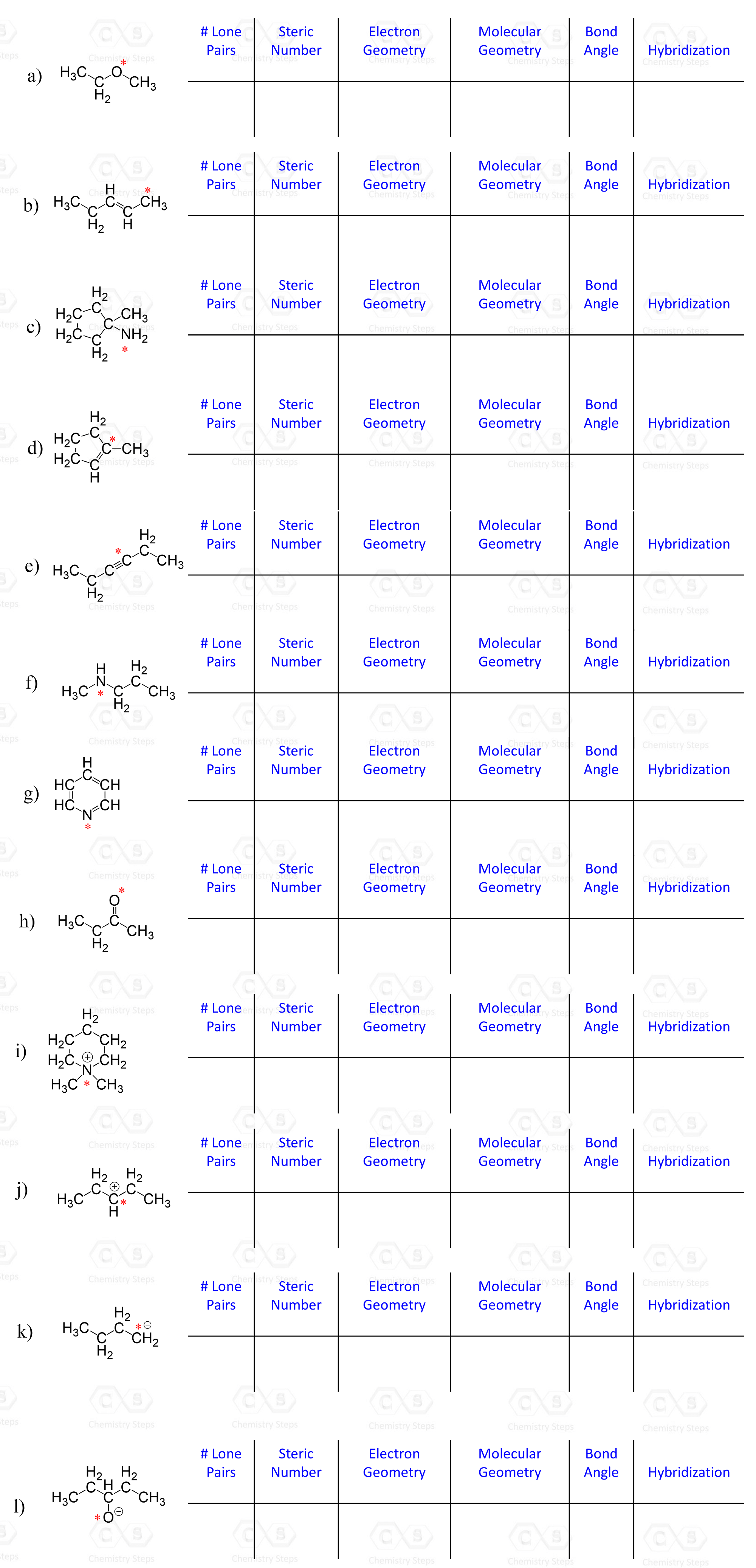
Determine the hybridization state of each carbon and heteroatom (any atom except C and H) in the following compounds.
Hint: Remember to add any missing lone pairs of electrons where necessary.

Check Also
- Lewis Dot Symbols
- The Ionic Bond
- The Covalent Bond
- Sigma and Pi Bonds
- Electronegativity and Bond Polarity
- The Octet Rule
- Formal Charges
- Lewis Structures and the Octet Rule
- Lewis Structures Practice Problems
- Resonance Structures
- The VSEPR Model
- VSEPR Theory Practice Problems
- sp, sp2, sp3, sp3d, and sp3d2Hybridization Practice Problems
