The VSEPR (valence shell electron pair repulsion) theory predicts the geometry of atoms or molecules. It is based on the principle that atoms and lone pairs repel each other because of electrostatic forces and thus, they are positioned as far away as possible to give the molecule an optimal geometry. To determine the geometry, we count the sum of the number of atoms and lone pairs around the central atom. This number is called the electron groups (EG) or steric number (SN) and it defines the geometry of the molecule.
Steric Number
For example, let’s determine the steric number of Be in BeCl2. The first thing you need to do is draw the Lewis structure including all the lone pairs of electrons if there are any. Here are the summary steps for drawing Lewis structures, and if you need to review it, go over the article here.
1. Write the correct skeletal structure for the molecule.
* Hydrogen atoms are always terminal (only one bond)
* Put more electronegative elements in terminal positions
2. Sum the valence electrons from all the atoms.
3. Use a pair of electrons to form a bond between each pair of bound atoms.
4. Add the remaining electrons to satisfy the octet for more electronegative atom first.
5. If any atoms lack an octet, make a double or triple bond to give them an octet.
So, the first step is to draw the correct skeletal structure. Beryllium is the central atom and, therefore, the structure would be:
There is a total of 2 + 2×7 = 16 valence electrons, and we use four of them to make the bonds. The remaining 12 go on the Cl atoms as lone pairs:
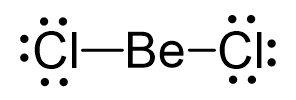
Because the Be has only two atoms and no lone pairs, its steric number is two. Notice that we do not count the lone pairs on the Cl atoms, since we are determining the geometry of the central atom. Another important thing you need to remember is that it does not matter whether the central atom is connected with single, double, or triple bonds – we only count the number of atoms and lone pairs it bears.
For example, the steric number of carbon in HCN is still two even though it is connected with the nitrogen via a triple bond:
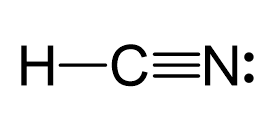
So, once again, keep in mind that multiple bonds do not matter – we treat them as single bonds and only count the atoms and lone pairs for the electron group/steric number.
Let’s put a little chart of example for steric number ranging from 2-6:
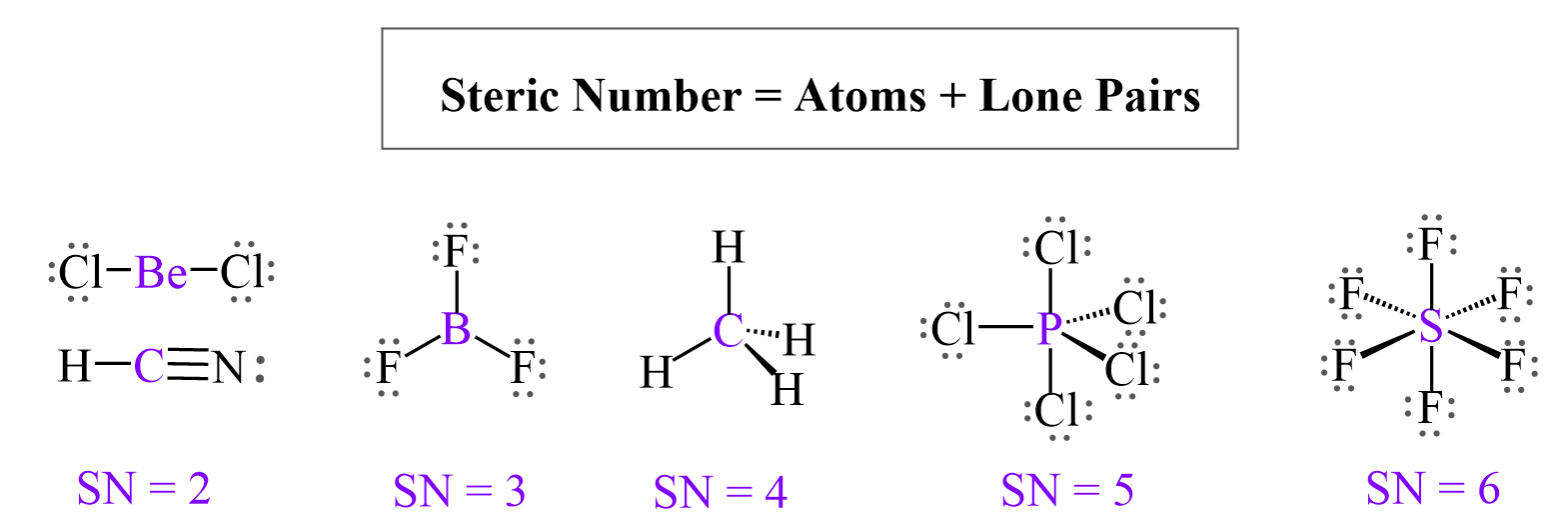
Now, it is not always that the central atom has no lone pairs, and we only need to worry about the number of atoms. For example, the oxygen in water has two atoms (hydrogens) connected to it, but when determining is geometry, we need to also consider the effect of the two lone pairs:
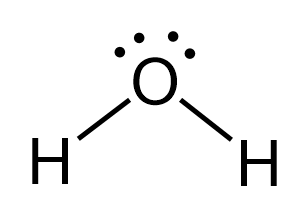
To make this easier, we can classify the compounds into two groups: the ones with lone pairs on the central atoms, and the ones without them.
Central Atoms with no Lone Pair(s)
For central atoms with no lone pairs, there are 5 molecular geometries and approximate bond angles you need to know.
So, let’s discuss these geometries in a little more detail.
Two Atoms – Linear Geometry
We have seen how the BeCl2 adopts a linear geometry because of the two Cl atoms on the Be. Another example is carbon dioxide, CO2:
This molecule also has a linear geometry because the carbon has only two atoms and no lone pairs on it.
Three Atoms – Trigonal Planar Geometry
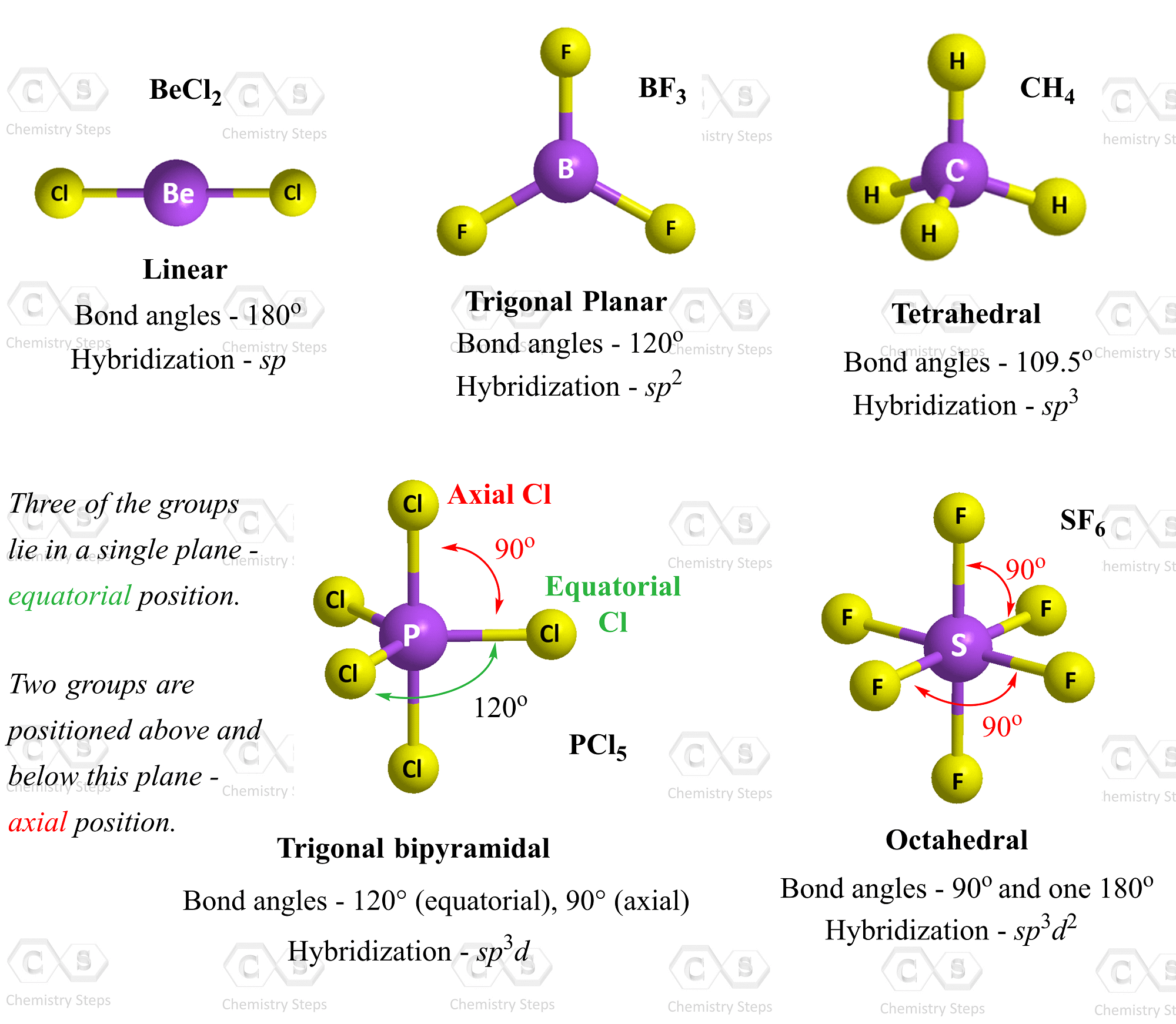
Boron is the central atom, so we can draw the skeletal structure as:
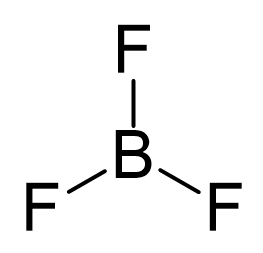
There is a total of 3 + 3 x 7 = 24 electrons, and halogens on terminal positions are always going to have 3 lone pairs of electrons. Therefore, 3 x 6 = 18 electrons on the fluorenes, and the remaining 6 are used to make the three covalent bonds:
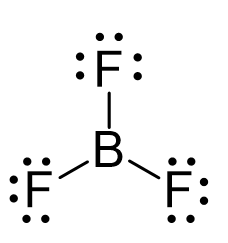
The central atom has three bonds and no lone pairs, therefore, both the electron and molecular geometries are trigonal planar. The bond angle between the fluorine atoms is 120o.
The steric number (the sum of the number of the atoms and lone pairs) of B is 3 which corresponds to sp2-hybridization.
Four Atoms – Tetrahedral Geometry
The most common example of an atom with four atoms and no lone pairs is methane. CH4.
This is the Lewis structure of methane, and one may expect that the bond angles should be 90o. However, it turns out that there is a geometry that allows for a more optimal arrangement of four atoms, and it is called tetrahedral geometry. The advantage is that the bond angle between the groups is 109.5o unlike the 90o we see in the Lewis structure.
Five Atoms – Trigonal Bipyramidal Geometry
The best arrangement for five groups around the central unit is achieved with trigonal bipyramidal geometry. An example of trigonal bipyramidal geometry is the molecule PCl5:
Notice that not all the angles in the trigonal bipyramidal structure are same. This is because the geometry is not as symmetrical, and we have two positions: equatorial and axial. From this view, the equatorial positions are pointing to the sides and the angles between the equatorial positions are 120°. The axial positions are on the bottom and the top. The angle between these two is 180o whereas the angle between the axial and equatorial positions is 90°.
Six Atoms – Octahedral Geometry
When six atoms are connected to a central atom, it adopts what is called octahedral geometry. A good example in general chemistry is sulfur hexafluoride, SF6:
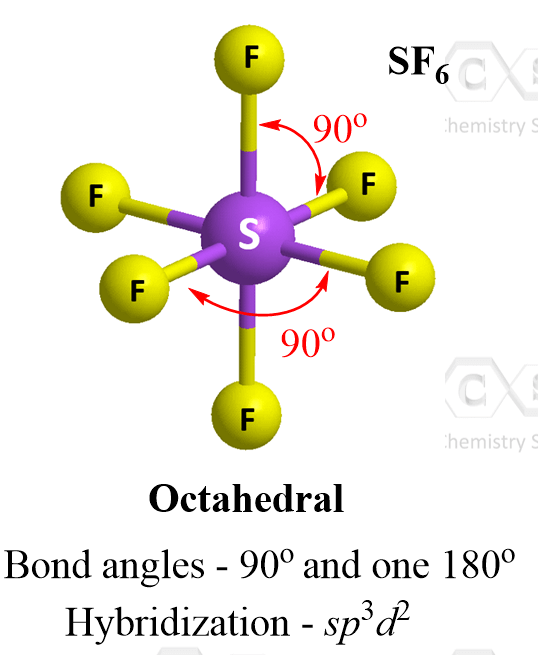
Four of the groups lie in a single plane, and the other two are above and below it. The angles between all neighboring groups 90° while the ones separated with an atom is 180o.
Molecular and Electron Geometry
Before we get to the geometry of molecules with lone pair(s), you need to know that a structure is characterized by molecular and electron geometry, which sometimes may be the same. So, when is the “sometimes” you may ask? For all the examples, where the central atom has no lone pair, the electron and molecular geometries are the same.
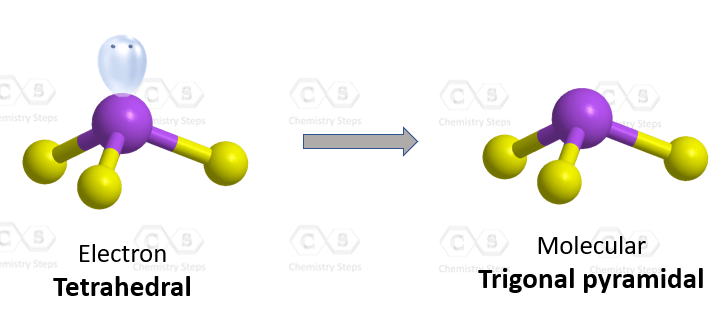
However, the presence of a lone pair(s) affects the geometry and therefore, the naming strategy of the molecule. For example, the electron geometry of ammonia, NH3 is tetrahedral while the molecular geometry is trigonal pyramidal:
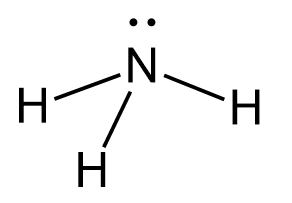
Let’s first see the significance of the lone pair on nitrogen. It is important as if it wasn’t there, we would have a hypothetic molecule with a flat/planar geometry:
Now, for the electron geometry, we do everything as seen before. That is count the number of atoms and lone pairs and name it according to the steric number. For the molecular geometry, we keep the shape as it is, but we ignore the lone pairs. This brings a few new names such as the trigonal pyramidal which we have not seen in the five geometries mentioned earlier.
Why do we ignore the lone pair for naming the molecular geometry? One way to look at it is the fact that electrons are infinitely smaller and lighter than nuclei and when looking on modern microscopes, we don’t see them.
Let’s now go over the examples of structures with lone pairs and see how the names of electron and molecular geometries vary.
Four Electron Groups with Lone Pairs
We just saw the example of ammonia as a molecule with three atoms and one lone pair.
Again, the central atom has 3 atoms and a lone pair (SN = 4). Therefore, the electron geometry is tetrahedral while the molecular geometry is trigonal pyramidal:
It is important to know that a lone pair has a greater repulsion than a bonding pair of electrons (bonding pair means an atom in this context). If all the groups in a tetrahedral geometry are the same, then the angle is 109.5o as we have seen for methane. However, in ammonia, the angle between the hydrogen atoms is smaller, 107o because of the greater repulsion of the lone pair.
Two Atoms and Two Lone Pairs
The example here has to be water:
The central atom has a steric number of 4 – two atoms and two lone pairs, and therefore, the electron geometry, therefore, is tetrahedral, and the molecular geometry is bent.
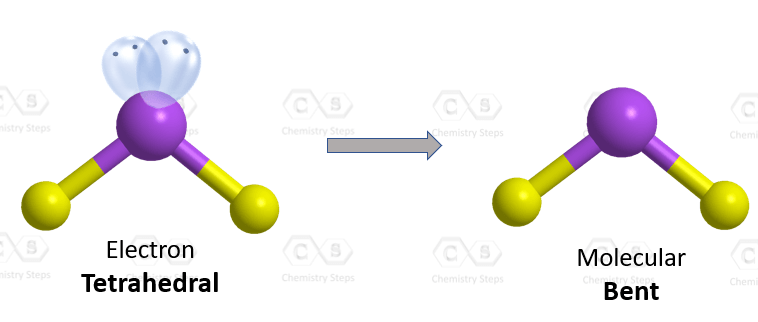
As expected, the two lone pairs make the bond angle between the hydrogen atoms even smaller bringing it down to 104.5o.
Five Electron Groups with Lone Pairs
Four Atoms and One Lone Pair: Let’s consider the Lewis structure of SF4:
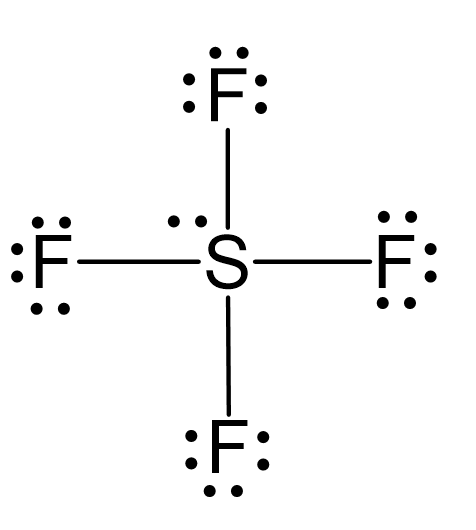
The steric number of sulfur is 4 +1 = 5, and therefore, the electron geometry is trigonal bipyramidal.
To determine the molecular geometry, we need to ignore the lone pair and see what shape is obtained. What we need to know though is where the lone pair is in the first place. Is it in an axial or equatorial position? Because lone pairs exert larger repulsive forces, it is favorable for them to occupy an equatorial position. This puts them at 120o relative to the other equatorial groups and there are only two groups (axial and equatorial) that are at 90o. On the other hand, if the lope pair was in an axial portion, it would have three 90° interactions with bonding pairs.
So, when the lone pair in the equatorial position is disregarded, a molecular geometry is seen which is called a seesaw:
Three Atoms and Two Lone Pairs
Another example of trigonal bipyramidal electron geometry is BrF3:
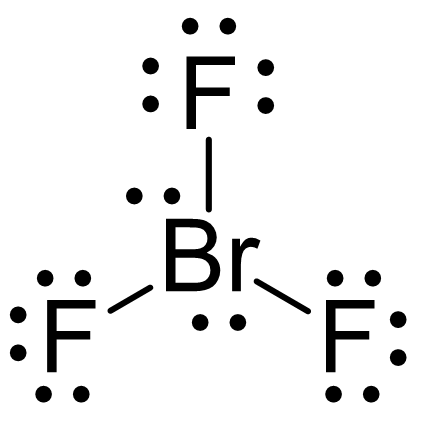
The difference with SF4 is that it has two lone pairs in the equatorial position, and therefore, the molecular geometry is called T-shaped:
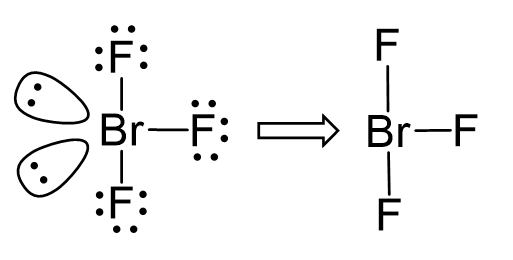
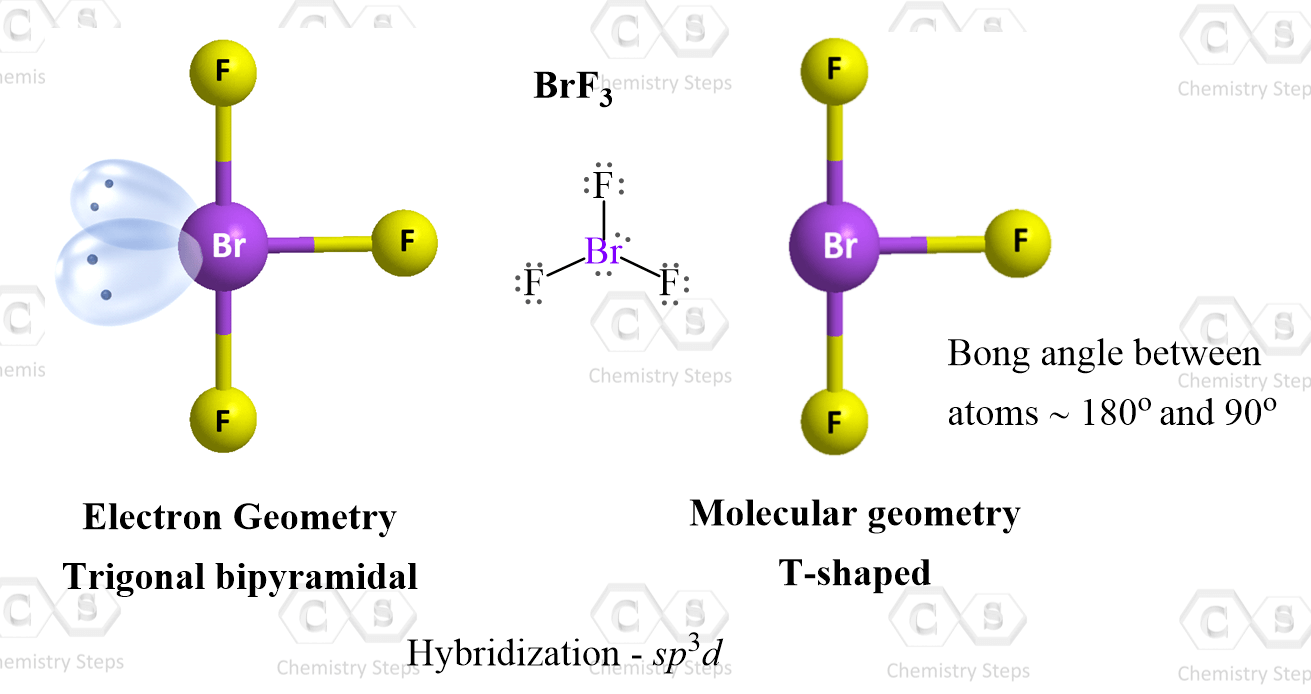
Two Atoms and Three Lone Pairs
Consider the Lewi structure of XeF2:
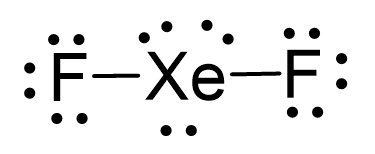
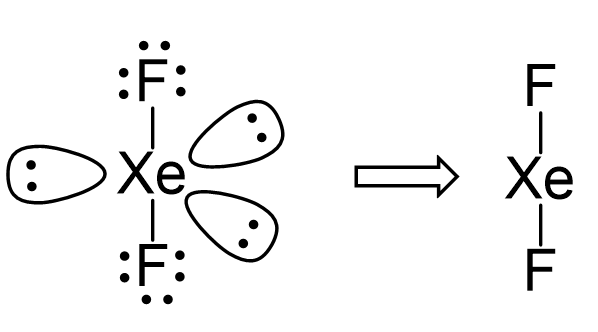
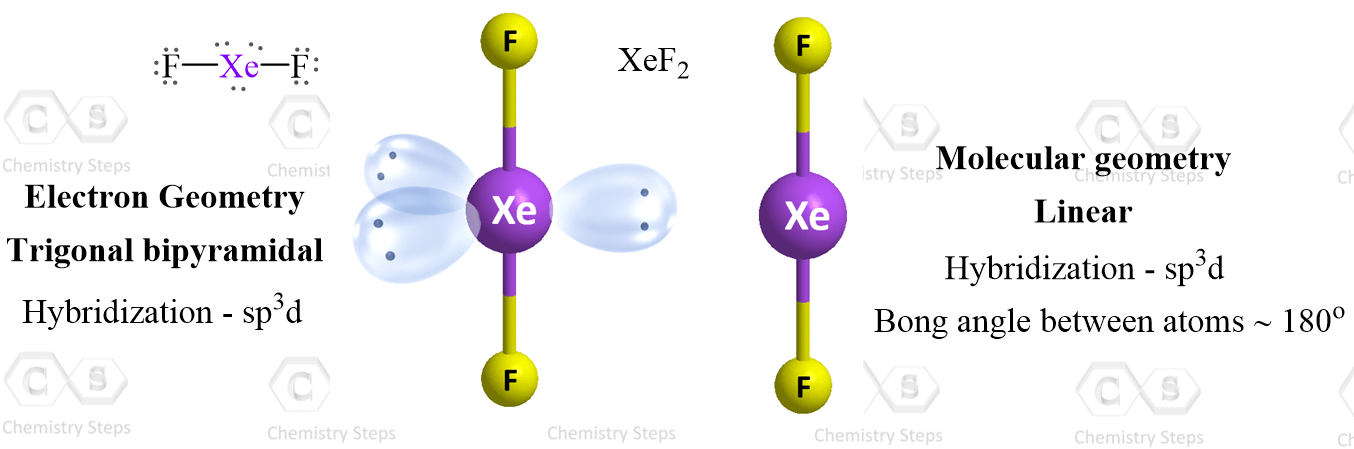
There are 5 units around the central atom, and therefore, the electron geometry is trigonal bipyramidal while the molecular geometry is linear.
Six Electron Groups with Lone Pairs
Two Atoms and Three Lone Pairs:
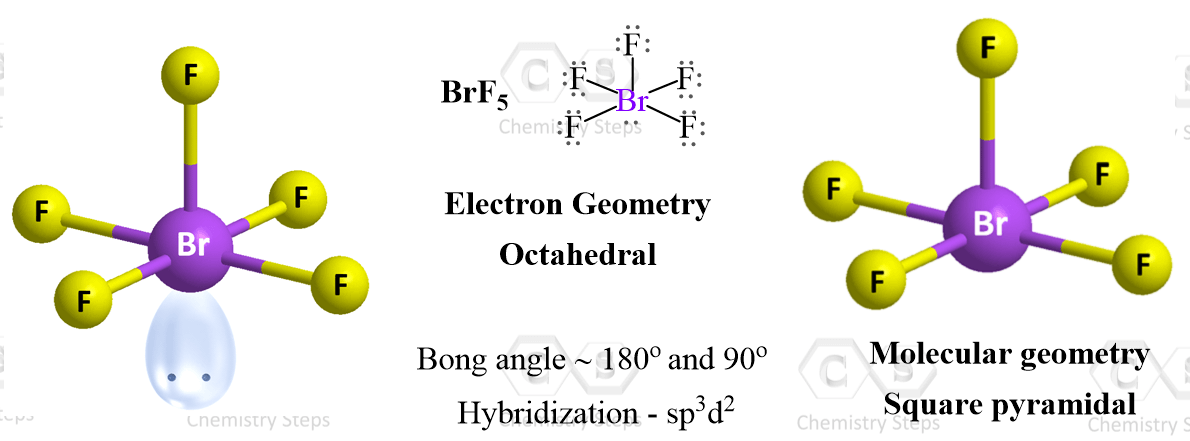
Let’s consider the Lewis structure of BrF5:
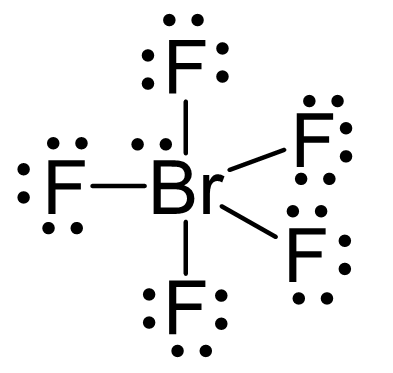
The central atom is bromine which is surrounded by six electron groups – five atoms and one lone pair. Because the steric number is six, the electron geometry, due to the six electron groups, is octahedral. The geometry is symmetrical and therefore, all six positions are equivalent which makes it possible to put the lone pair(s) in any one of these positions.
When there is only one lone pair like in BrF5, the resulting molecular geometry is called square pyramidal.
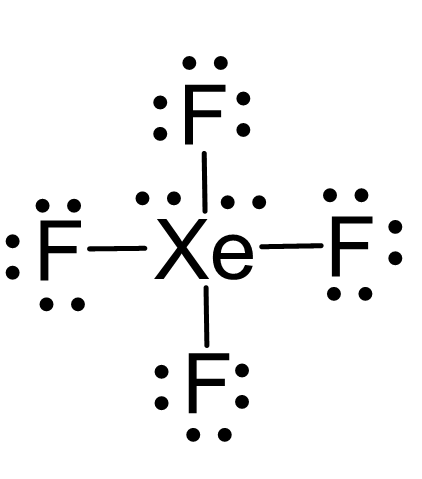
Four Atoms and Two Lone Pair
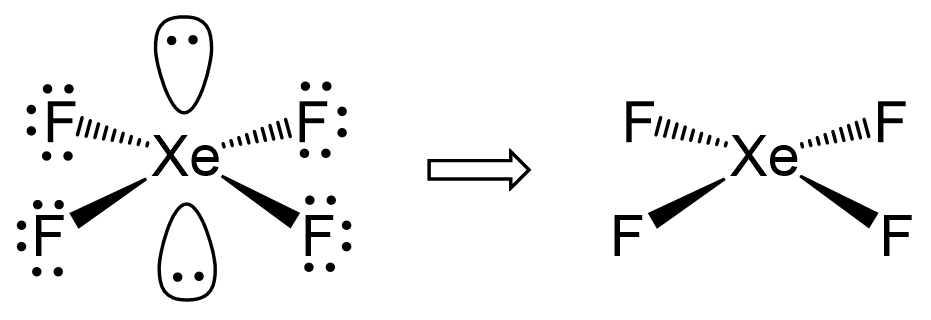
Xef4 falls into this category as the central atom has four atoms and two lone pairs:
There are 6 units around the central atom, and therefore, the electron geometry is octahedral while the molecular geometry is square planar.
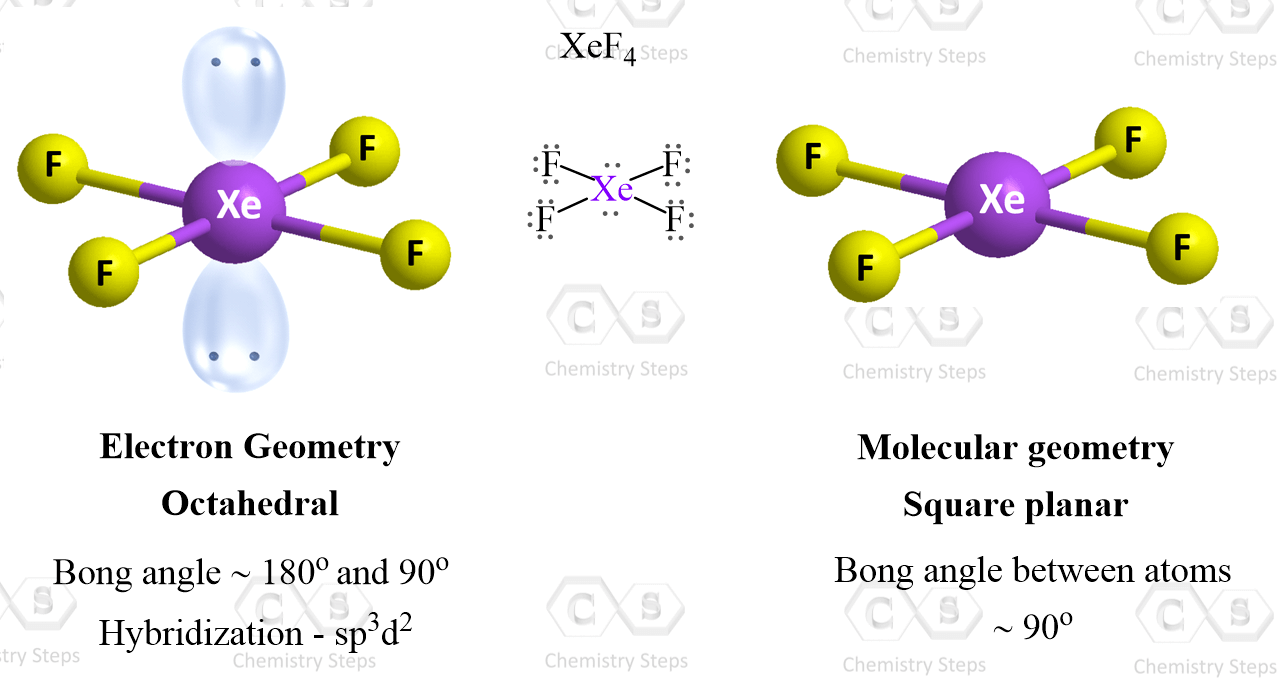
In the end, I would like to mention that there is a separate post on VSEPR theory tailored toward organic molecules. On one hand, it is a little easier since carbon, the main element in organic chemistry, only makes four bonds at most, and therefore, the steric number goes up to 4.
On the other hand, a lot of organic molecules are larger, and studying their structures takes new skill sets.
Practice
Determine the electron geometry and molecular geometry of the following molecules using the VSEPR model.
| (a) BF3 | (b) CH2O | (c) HCN | (d) BeCl2 | (e) CH2Cl2 |
| (f) SOCl2 | (g) SO2 | (h) PCl5 | (i) XeO4 | (j) NCl3 |
| (k) SiCl4 | (l) SF2 | (m) H2S | (n) SO3 | (o) COCl2 |
| (p) PCl3 | (q) OF2 | (r) BrF5 | (s) N2O | (t) SF6 |
| (u) POCl3 | (x) XeF2 | (y) XeF4 | (z) C2H2 |
Follow these steps to determine the electron and molecular geometries:
- Determine the central atom and draw the Lewis structure for the molecule.
- Count the number of atoms and lone pairs of electrons on the central atom (steric number)
- Arrange them in a way that minimizes repulsion (as far apart as possible).
- Determine the name of the electron and molecular geometry.
To draw the Lewis structures:
- Write the correct skeletal structure for the molecule.
* Hydrogen atoms are always terminal (only one bond)
* Put more electronegative elements in terminal positions
- Sum the valence electrons from all the atoms.
- Use a pair of electrons to form a bond between each pair of bound atoms.
- Add the remaining electrons to satisfy the octet for a more electronegative atom first.
- If any atoms lack an octet, make a double or triple bond to give them an octet.
(a) BF3 – trigonal planar, trigonal planar
B is the central atom:
There is a total of 3 + 3 x 7 = 24 electrons, and halogens on terminal positions are always going to have 3 lone pairs of electrons. Therefore, 3 x 6 = 18 electrons on the fluorenes and the remaining 6 are used to make the three covalent bonds:
The central atom has three bonds and no lone pairs, therefore, both the electron and molecular geometries are trigonal planar.
(b) CH2O – trigonal planar, trigonal planar
The carbon is the central atom:
There is a total of 4 + 2×1 + 6 = 12 electrons, and 6 are already used for making the bond. The remaining 6 go to oxygen as it is the most electronegative atom.
Because the carbon lacks an octet, we use one lone pair from the oxygen to make a π bond with the carbon, and thus, a double bond is formed.
The central atom has three bonds and no lone pairs, therefore, both the electron and molecular geometries are trigonal planar.
In general, remember that oxygens on terminal positions are always going to have 2 bonds and 2 lone pairs of electrons unless there is a formal charge on them.
Knowing these patterns for bonding, lone pairs, and formal charges will make these types of exercises a lot easier.
(c) HCN – linear, linear
Carbon is the central atom:
There is a total of 1 + 4 + 5 = 10 valence electrons, and we use four of them to make the bonds.
The remaining 6 go on the nitrogen as lone pairs:
Because the carbon lacks an octet, we use two lone pairs from the nitrogen to make two additional bonds:
The steric number is 2, and there are no lone pairs on the central atom. Therefore, both geometries are linear.
(d) BeCl2 – linear, linear
Be is the central atom:
There is a total of 2 + 2×7 = 16 valence electrons, and we use four of them to make the bonds. The remaining 12 go on the Cl atoms as lone pairs:
The steric number is 2, and there are no lone pairs on the central atom. Therefore, both geometries are linear.
(e) CH2Cl2 – tetrahedral, tetrahedral
Carbon is the central atom:
There are 4 + 2 + 2×7 = 20 electrons, and 8 have been used to make four bonds. The remaining 12 go on the two chlorines as lone pairs:
The central atom has four atoms and no lone pair, therefore, both the electron and molecular geometries are tetrahedral:
(f) SOCl2 -tetrahedral, trigonal pyramidal
(f) Sulfur is the central atom, so we can draw the skeletal structure:
There are 6 + 6 + 2×7 = 26 electrons, and 6 are used to make 3 bonds. Two chlorines and the oxygen take 3 lone pairs, and the remaining one goes to the sulfur:
All the atoms have an octet, however, there are three lone pairs on the oxygen which gives it a -1 formal charge. Therefore, one of the lone pairs on the oxygen is used to make another bond with the sulfur, and even if it exceeds the octet, that is acceptable for elements in the third row and below because they have d orbitals.
The central atom has 3 atoms and a lone pair (SN = 4). Therefore, the electron geometry is tetrahedral while the molecular geometry is trigonal pyramidal:
(g) SO2 – trigonal planar, bent
Sulfur is the central atom, so we can draw the skeletal structure:
There are 3×6 = 18 electrons, and 4 of them are used to make 2 bonds. The two oxygens take 6 lone pairs, and the remaining one goes to the sulfur:
As it is drawn, the problems with this structure are that the sulfur lacks an octet and the oxygens have only one bond and three lone pairs. Remember, the normal valency of oxygens is having two bonds and two lone pairs otherwise a formal charge needs to be assigned.
Therefore, one lone pair from each oxygen is used to make an additional bond with the sulfur:
The central atom has a steric number of 3 – two atoms and one lone pair. The electron geometry, therefore, is trigonal planar, and the molecular geometry is bent.
(h) PCl5 – trigonal bipyramid, trigonal bipyramid
Phosphorous is the central atom:
There are 5×7 + 5 = 40 electrons, out of which, 10 are used to make 5 covalent bonds. All the remaining 30 are divided between the five chlorine atoms, each taking 6 electrons as 3 lone pairs:
There are 5 atoms and no lone pairs on the central atom, therefore, both geometries are trigonal bipyramidal:
(i) XeO4 – tetrahedral, tetrahedral
Xe is the central atom:
There are 4×6 + 8 = 32 electrons and this time, instead of putting three lone pairs on the oxygen, we are going to directly add double bonds to leave two lone pairs for each oxygen:
All the electrons are used: 4 double bonds = 16, 8 lone pairs = 16.
The central atom has four atoms and no lone pair, therefore, both the electron and molecular geometries are tetrahedral.
(j) NCl3 – tetrahedral, trigonal pyramidal
N is the central atom and there are 5 + 3×7 = 26 electrons. Each chlorine taking three lone pairs leaves the nitrogen with one lone pair:
The central atom has 3 atoms and a lone pair (SN = 4). Therefore, the electron geometry is tetrahedral while the molecular geometry is trigonal pyramidal:
(k) SiCl4 – tetrahedral, tetrahedral,
Silicon is the central atom:
There are 4 + 4×7 = 32 electrons, and 8 have been used to make four bonds. The remaining 24 go on the two chlorines as lone pairs:
The central atom has four atoms and no lone pair, therefore, both the electron and molecular geometries are tetrahedral:
(l) SF2 – tetrahedral, bent
Sulfur is the central atom. There are 6 + 2×7 = 20 electrons, and 4 of them are used to make 2 bonds. The two fluorines take 6 lone pairs, and the remaining four electrons go to the sulfur:
The central atom has a steric number of 4 – two atoms and two lone pairs. The electron geometry therefore, is tetrahedral, and the molecular geometry is bent.
(m) H2S – tetrahedral, bent
Sulfur is the central atom:
There are 6 + 2 = 8 electrons, and 4 of them are used to make 2 bonds. The remaining four electrons go to the sulfur:
The central atom has a steric number of 4 – two atoms and two lone pairs. The electron geometry, therefore, is tetrahedral, and the molecular geometry is bent.
(n) SO3 – trigonal planar
Sulfur is the central atom:
There are 3×6 + 6 = 24 electrons, and 6 of them are used to make 3 bonds. Three oxygens take 6 lone pairs and make an additional bond with the sulfur.
All the electrons have been used, and the steric number of the central atom is 3 with no lone pairs. Therefore, both geometries are trigonal planar.
(o) COCl2 – Trigonal planar, trigonal planar
The carbon is the central atom:
There is a total of 4 + 2×7 + 6 = 24 electrons, and 6 are already used for making the bond. The remaining 18 go to oxygen and the chlorine atoms as lone pairs. Because the carbon lacks an octet, we use one lone pair from the oxygen to make a π bond with the carbon, and thus, a double bond is formed.
The central atom has three atoms and no lone pairs, therefore, both the electron and molecular geometries are trigonal planar.
(p) PCl3 – tetrahedral, trigonal pyramidal
P is the central atom and there are 5 + 3×7 = 26 electrons. Each chlorine taking three lone pairs leaves the nitrogen with one lone pair:
The central atom has 3 atoms and a lone pair (SN = 4). Therefore, the electron geometry is tetrahedral while the molecular geometry is trigonal pyramidal:
(q) OF2 – tetrahedral, bent
Oxygen is the central atom:
There are 6 + 2×7 = 20 electrons, and 4 of them are used to make 2 bonds. The two fluorines take 6 lone pairs, and the remaining four electrons go to the sulfur:
The central atom has a steric number of 4 – two atoms and two lone pairs. The electron geometry therefore, is tetrahedral, and the molecular geometry is bent.
(r) BrF5 – Octahedral ,Square pyramidal
Br is the central atom:
There are 5×7 + 7 = 42 electrons, out of which, 10 are used to make 5 covalent bonds. The remaining 30 are divided between the five fluorine atoms, each taking 6 electrons as 3 lone pairs, and Br takes the last pair of electrons:
There are 5 atoms and one lone pair on the central atom, therefore, the electron geometry is octahedral, while the molecular geometry is square pyramidal:
(s) N2O – linear, linear
Oxygen is more electronegative, therefore, it goes in a terminal position:
There are 2×5 + 6 = 16 valence electrons and four are already taken to make two bonds. The remaining 12 are distributed between the oxygen and nitrogen:
Because the middle nitrogen lacks an octet, two lone pairs from the nitrogen are used to make two pi bonds with the middle nitrogen and the Lewis structure of this compound can be given as follows:
There are formal charges here because the middle nitrogen and the oxygen are not in their common bonding pattern:
This is one resonance structure and the other would be:
There are formal charges here because the middle nitrogen and the oxygen are not in their common bonding pattern:
This is one resonance structure and the other would be:
In both cases, the central atom has two atoms and no lone pairs, therefore, both geometries are linear.
(t) SF6 Octahedral , Octahedral ,
Sulfur is the central atom:
There are 6 + 6×7 = 48 valence electrons, and 12 are taken for making 6 covalent bonds. Each fluorine takes three lone pairs, so there are no electrons left: 48 – (12 + 6×6) = 0.
The central atom has 6 atoms connected to it, and no lone pairs, therefore, both geometries are octahedral:
(u) POCl3 – tetrahedral, tetrahedral
P is the central atom:
There are 5 + 3×7 + 6 = 32 valence electrons out of which, 8 are already taken to make four covalent bonds. From the remaining 24, 18 go to the Cl atoms as three lone pairs per each, three 6 to the oxygen as three lone pairs. This leaves the central atom with 4 atoms connected to it and no lone pairs. Therefore, both geometries are tetrahedral.
(v) SF4 trigonal bipyramid, seesaw
Sulfur is the central atom:
There are 6 + 4×7 = 34 valence electrons, and 8 are taken for making 4 covalent bonds. Each fluorine takes three lone pairs, so there are 34 – (8 + 4×6) = 2 electrons left which go the sulfur as a lone pair:
The central atom has 4 atoms connected to it, and one lone pair, therefore, the electron geometry is trigonal bipyramidal while the molecular geometry is seesaw:
Notice that the lone pair does not go an axial position (up or down).
(w) BrF3 – Trigonal bipyramidal, T-shaped
Br is the central atom:
There are 7 + 3×7 = 28 electrons and 6 are taken to make three covalent bonds. Each fluorine takes 6 electrons, therefore there are 28 – (6 + 3×6) = 4 electrons left, which go on the Br as two lone pairs:
The central atom has 3 atoms and 2 lone pairs, therefore, the electron geometry is trigonal bipyramidal, while the molecular geometry is T-shaped:
Notice that the lone pair does not go in axial positions (up or down).
(x) XeF2 – Xe is the central atom:
There are 2×7 + 8 = 22 electrons and 4 are taken to make 2 covalent bonds. Each fluorine takes 3 lone pairs, so there are 22 – (4+2×6) = 6 electrons left which go to Xe as 3 lone pairs:
There are 2 atoms and 3 lone pairs on the central atom, so the steric number is 5, and therefore, the electron geometry is trigonal bipyramidal and the molecular geometry is liner:
(y) – XeF4 – Xe is the central atom:
There are 4×7 + 8 = 36 electrons and 8 are taken to make 4 covalent bonds. Each fluorine takes 3 lone pairs, so there are 36 – (8+4×6) = 4 electrons left which go to Xe as 2 lone pairs:
There are 4 atoms and 2 lone pairs on the central atom, therefore, the steric number is 6 and the electron geometry is octahedral and the molecular geometry is square planar:
(z) – C2H2 linear, linear
Because the hydrogens are always in terminal positions, the carbons must be connected, and therefore, we can draw a preliminary skeletal structure to start with:
There are 2×4 + 2×1 = 10 valence, and 6 have been used to make 3 covalent bonds. Therefore, the remaining 4 go to the carbon atoms as lone pair on each:
The carbons atoms are lacking octet, so we use the two lone pairs for making 2 additional bonds between them:
Even though there is no single central atom, both carbons are linear since their steric number is 2 which makes the molecule linear as well.
Additionally, if you have covered the hybridization theory, you should recognize that both carbons are sp-hybridized and thus the bond angle is 180o which makes the molecule linear.
Determine the electron and molecular geometry of each ion using the VSEPR theory: (a) NH4+, (b) H3O+, (c) CN– (d) SCN–, (e) CO32-, (f) ClO3–, (g) SO42- (h) PO43- (i) SO32– (j) NO2– (k) BF4– (l) NO3–.
| (a) NH4+ | (b) H3O+ | (c) CN– | (d) SCN– | (e) CO32- |
| (f) ClO3– | (g) SO42- | (h) PO43- | (i) SO32– | (j) NO2– |
| (k) BF4– | (l) NO3– |
(a) NH4+,
Nitrogen is the central atom:
There is a positive charge, so to determine the number of electrons, we subtract 1 from the total number of valence electrons:
5 + 4 – 1 = 8 electrons
All the electrons are used to make the 4 covalent bonds, and the positive charge is on the nitrogen:
Remember, the formula for calculating the formal charge:
FC= V – (N + B)
Where:
V – number of valence electrons
N – number of nonbonding electrons
B – number of bonds
So, for the nitrogen it would be: 5 – (0 + 4) = +1
Try memorizing the bonding and formal charge patterns to make this process easier:
For the geometry, the nitrogen has 4 atoms and no lone pairs, therefore, both geometries are tetrahedral.
The central atom is the oxygen:
The total number of electrons is 6 + 3 – 1 = 8, out of which, 6 are used to make three covalent bonds, and one goes to the oxygen as a lone pair. The oxygen is positively charged since it only has one lone pair of electrons:
There are 3 atoms and one lone pair on the central atom, therefore, the electron geometry is tetrahedral, and the molecular geometry is trigonal pyramidal.
Connect the atoms together and count the number of electrons by adding 1 since there is a negative charge:
#e– = 4 + 5 + 1 = 10
Two electrons are used to make the covalent bond, therefore, the remaining 8 go to nitrogen as 3 lone pairs, and two to the carbon as a lone pair:
Use two lone pairs from the nitrogen to make a triple bond with the carbon which is left with a lone pair and therefore, a negative charge:
Two atoms have one atom connected and therefore, both geometries are linear. Additionally, notice that the hybridization state for the C and N is sp which implies a linear geometry.
Carbon is the central atom:
There are 6 + 4 + 5 + 1 = 16 electrons, and 4 are already taken to make two covalent bonds. The remaining 12 are divided between the S and N as 3 lone pairs:
One possibility is to use two lone pairs from the nitrogen, and the other is to once form the nitrogen and one form the sulfur:
These two are resonance forms of the same compound either one gives a linear electron molecular geometry because the central atom has two atoms and no lone pairs.
There are 4 + 3×6 + 2 = 24 electrons. The carbon goes in the middle, and the oxygens take 6 electron each as three lone pairs:
The carbon lacks an octet, so we use a lone pair from one oxygen to make a double with it. The other two oxygen are then negatively charged:
The central atom has 3 atoms and no lone pairs, therefore, both geometries are trigonal planar.
There are 7 + 3×6 + 1 = 26 electrons. The chlorine goes in the middle with one lone pair, and the oxygens take 6 electrons each as three lone pairs:
As drawn, the oxygens are going to be negatively charged, which would mean a -3 ionic charge. Therefore, two oxygen will use one of their lone pairs to make a double with the chlorine. The other oxygen is then negatively charged:
The central atom has 3 atoms and one lone pair, therefore, the electron geometry is tetrahedral and the molecular geometry is trigonal pyramidal.
Sulfur is the central atom:
There are 4×6 + 6 + 2 = 32 electrons, and 8 of them are used to make 4 bonds. The four oxygens take 3 lone pairs each and no electrons are left:
All the electrons have been used; however, two oxygens need to share a pair of electrons with the sulfur otherwise the ionic would be -4:
The central atom has 4 atoms and no lone pairs therefore, both geometries are tetrahedral.
Phosphorous is the central and there are 5 + 4×6 + 3 = 32 electrons. Give each oxygen three lone pairs:
All the electrons are used and the only thing to fix is the ionic charge. As drawn, it would be a -4, therefore, we give one lone pair from an oxygen to make a double bond with the P which can exceed the octet:
The central atom has four atoms and no lone pairs, therefore, both geometries are tetrahedral.
Sulfur is the central atom:
There are 3×6 + 6 + 2 = 26 electrons, and 6 of them are used to make 3 bonds. Three oxygens take 3 lone pairs each and one goes to the sulfur:
All the electrons have been used; however, one oxygen needs to share a pair of electrons with the sulfur otherwise the ionic would be -3:
The central atom has 3 atoms and a lone pair and therefore, the electron geometry is tetrahedral while the molecular geometry is trigonal pyramidal.
Nitrogen is the central atom:
There are 5 + 2×6 + 1 = 18 electrons, and 4 are used to make the two covalent bonds. Both oxygens get 6 electrons as three lone pairs, and nitrogen gets one lone pair:
One lone pair from an oxygen is used to make a π bond with the nitrogen and thus making the ionic charge -1:
The central atom has two atoms and a lone pair; therefore, the electron geometry is trigonal planar, and the molecular geometry is bent.
B is the central atom:
There is a total of 3 + 4×7 + 1 = 32 electrons, and 8 are used to make the covalent bonds. Halogens on terminal positions are always going to have 3 lone pair of electrons, so 4×6 = 24 electrons go on the fluorenes. The boron has a -1 charge since it has four bonds and it is in group 3:
The central atom has 4 atoms and no lone pairs, therefore, both the electron and molecular geometries are tetrahedral.
Nitrogen is the central atom:
There are 5 + 3×6 + 1 = 24 electrons, and 6 are used to make the two covalent bonds. The oxygens get 6 electrons as three lone pairs:
One lone pair from an oxygen is used to make a π bond with the nitrogen and thus making the ionic charge -1:
The central atom has 3 atoms and no lone pairs; therefore, both geometries are trigonal planar.
For each molecular geometry, determine if there are any lone pairs on the central atom and name the molecular and electron geometries accordingly:
No lone pairs.
Electron geometry – trigonal planar
Molecular geometry – trigonal planar
One lone pair.
Electron geometry – tetrahedral
Molecular geometry – trigonal pyramidal
No lone pairs.
Electron geometry – tetrahedral
Molecular geometry – tetrahedral
Two lone pairs
Electron geometry – tetrahedral or trigonal planar
Molecular geometry – bent
One lone pair.
Electron geometry – trigonal bipyramidal
Molecular geometry – seesaw
Two lone pairs.
Electron geometry – trigonal bipyramidal
Molecular geometry – T-shaped
One lone pair.
Electron geometry – octahedral
Molecular geometry – square pyramidal
One lone pair.
Electron geometry – octahedral
Molecular geometry – square planar
a) The only theoretical possibility of having lone pair(s) is if the electron geometry was trigonal bipyramidal. However, remember, that the lone pairs do not go on the axial positions:
Therefore, there are no lone pairs in this geometry.
b) There must be one pair on the top otherwise the three groups would have been at 120o making a trigonal planar geometry.
c) No lone pairs here because the tetrahedral molecular geometry is not derived from any electron geometry. The four groups are arranged in the optimal geometry and there is simply no room for a lone pair in this geometry.
d) If there were no lone pair, the two groups/atoms would have been at 180o making a liner molecular geometry. Therefore, the two atoms are brought closer either by one or two lone pairs. If there is one lone pair, then the electron geometry is trigonal planar, and if there are two lone pairs, the electron geometry is tetrahedral.
e) There are four atoms and if there was no lone pair, they would have been arranged in a tetrahedral geometry. As it is, the electron geometry is trigonal bipyramidal where one lone pair is in the equatorial position.
f) There are 3 atoms and if there was no lone pair, they would have been arranged in trigonal planar geometry. As it is, this is a T-shaped molecular geometry and the electron geometry is trigonal bipyramidal with two lone pairs in the equatorial positions.
g) There are 5 atoms and if there was no lone pair, they would have been in trigonal bipyramidal geometry. Therefore, there is lone pair that pushes the groups at 90o. This corresponds to octahedral electron geometry and the molecular geometry is square pyramidal.
h) Four atoms without lone pair would form a tetrahedral geometry, but because they are at 90o, there must be two lone pairs which make it an octahedral electron geometry and square planar molecular geometry.
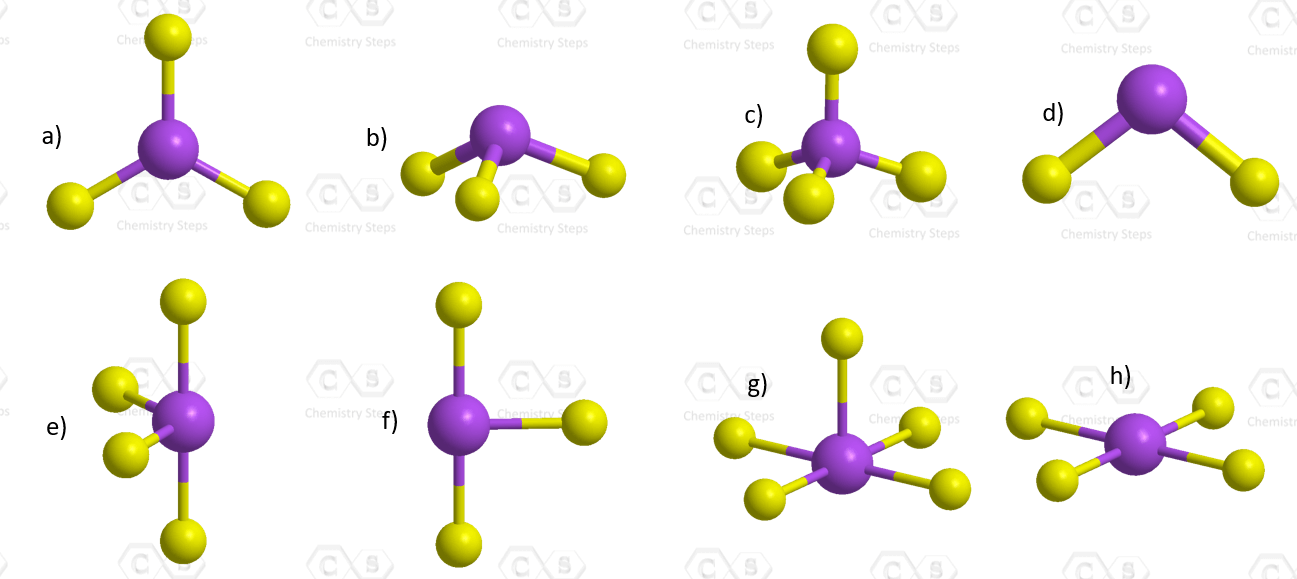
Below is shown the molecular geometry of ReF7. How would you name this geometry and what bond angles would you expect it to have?
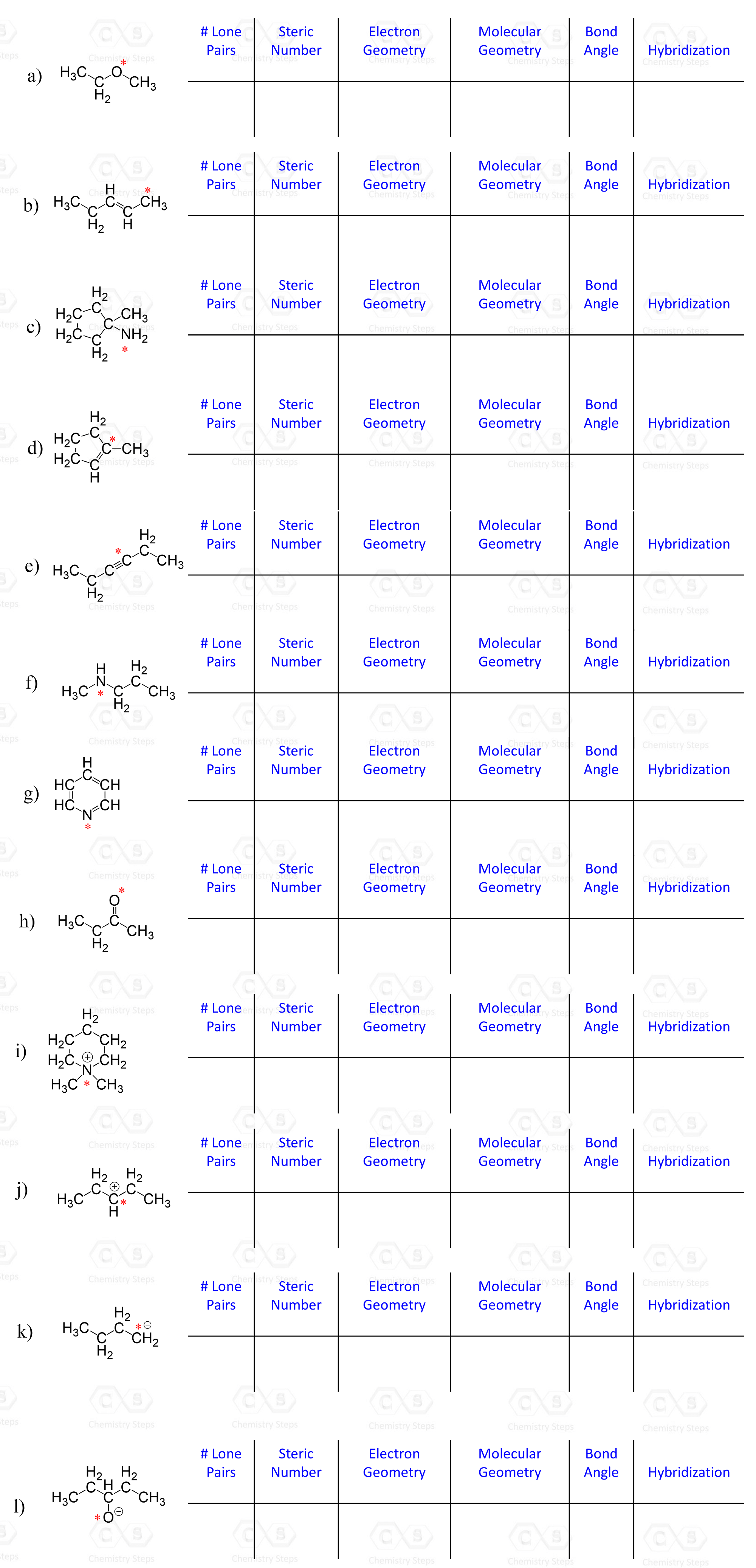
For each marked atom, add any missing lone pairs of electrons to determine the steric number, electron and molecular geometry, approximate bond angles, and the hybridization state.
You can also download the questions as a PDF worksheet to print and work on here.
Determine the molecular geometry of each marked atom in the following molecule:
a – bent
b – tetrahedral
c – linear
d – trigonal planar
e – trigonal pyramidal
a – There are two atoms and one lone pair on the nitrogen, so the steric number is 3. Therefore, the electron geometry is trigonal planar and the molecular geometry is bent.
b – there are four atoms and no lone pairs, therefore, the steric number is 4 and both geometries are tetrahedral.
c – There are two atoms and no lone pairs on the carbon, therefore, both geometries are linear.
d – There are three atoms and no lone pairs on the carbon, therefore, both geometries are trigonal planar.
e – There are three atoms and one lone pair on the nitrogen, therefore, the electron geometry is tetrahedral and the molecular geometry is trigonal pyramidal.
What is the molecular geometry of the nitrogen in the following molecules?
trigonal pyramidal
There are three atoms and one lone pair on the nitrogen, therefore, the electron geometry is tetrahedral and the molecular geometry is trigonal pyramidal.
What is the molecular geometry of the nitrogen in the following molecules?
bent
There are two atoms and one lone pair on the nitrogen, so the steric number is 3. Therefore, the electron geometry is trigonal planar and the molecular geometry is bent.
Determine the approximate bond angle in the following molecule:
120o
It is a trigonal planar geometry, therefore, the bond angles are about 120 o since not all the atoms are identical.
Determine the approximate bond angle in the following molecule:
180o
Both carbons with a triple bond are sp-hybridized with a linear geometry, therefore, the angle is 180o.
The angle between carbon 1 and 3 is:
109.5o
Carbon 1 and 3 are connected through carbon 2 which has tetrahedral geometry, so the bond angles are 109.5o.
The angle between carbon 2 and the lone pair on the nitrogen is:
120o
The nitrogen is sp2-hybridized with trigonal planar electron geometry. Therefore, the angle between the lone pairs and the carbon is about 120o.
Check Also
- Lewis Dot Symbols
- The Ionic Bond
- The Covalent Bond
- Sigma and Pi Bonds
- Electronegativity and Bond Polarity
- The Octet Rule
- Formal Charges
- Lewis Structures and the Octet Rule
- Lewis Structures Practice Problems
- Resonance Structures
- VSEPR Theory Practice Problems
- Hybridization of Atomic Orbitals
- sp, sp2, sp3, sp3d, and sp3d2Hybridization Practice Problems