In the previous post, we talked about the pH of buffer solutions and the two approaches to calculating it.
Let’s now discuss how to prepare a buffer with a given pH. So, we need to choose a proper acid/base pair with certain concentrations. When choosing the acid, remember that the acid should have a pKa as close to the desired pH value as possible.
This can be seen from the Henderson–Hasselbalch equation.
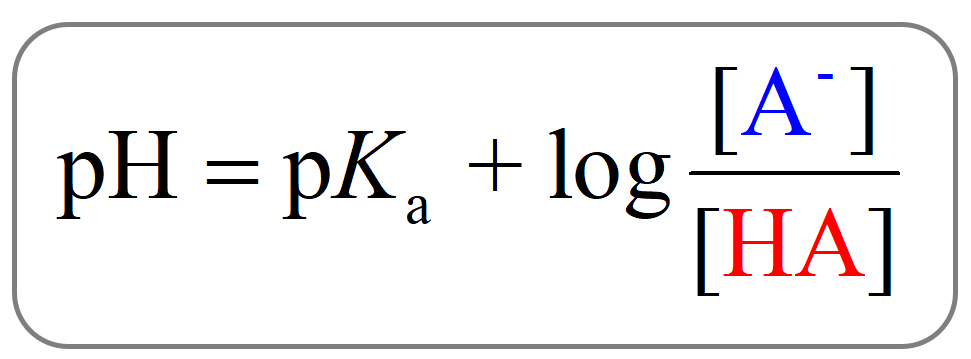
When [A–] = [HA], pH = pKa since the log term is equal to zero.
For example, if we need a buffer with pH = 4.75, an acid with a pKa close to 4.75 would be a great candidate.
The pKa of acetic acid is 4.75, and if a buffer solution contains, for example , 0.2 M CH3CO2– and 0.2 M CH3CO2H, the pH will be equal to the pKa:
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\]
\[{\rm{pH}}\; = \;4.75\; + \,\cancel{{{\rm{log}}\frac{{{\rm{0}}{\rm{.2}}\;{\rm{M}}}}{{{\rm{0}}{\rm{.2}}\;{\rm{M}}}}}}\; = \,4.75\]
So, how do we determine the ratio of A–/HA if the pH is different than the pKa of the acid with the closest value?
For example, let’s say we need a buffer solution with pH = 4.0.
The closest match is going to be the acetate buffer and to determine the [CH3CO2–]/[CH3CO2H] ratio required to prepare it, we need to rearrange the Henderson-Hasselbalch equation to obtain an expression for [CH3CO2–] and [CH3CO2H]:
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\]
Therefore,
\[{\rm{log}}\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{Na]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\;\; = \;{\rm{pH}}\; – \;{\rm{p}}{K_{\rm{a}}}\; = \;4.0\; – \;4.75\; = \; – 0.75\]
The antilog of this expression is:
antilog (-0.75) = 10-0.75 = 0.18
\[{10^{\left( {{\rm{log}}\frac{{[{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{Na}}]}}{{[{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H}}]}}} \right)}}\;\; = \;{10^{\left( { – 0.75} \right)}}\]
\[\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{Na]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\; = \;0.18\]
This means that, for example, if the solution contains 1.0 M CH3CO2H, the concentration of CH3CO2– would have to be 0.18 M.
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- The Common Ion Effect
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of a Common Ion on Solubility
- The Effect of pH on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems
