Le Châtelier’s principle states that a system at equilibrium does not want to be disturbed. So, if we try to interfere with a system at equilibrium, it will minimize the effect of the action to reestablish the equilibrium.
We can think of it as a balance swing. The springs keep it at a horizontal position which is the optimal state of the setup and if we push on either side, the spring forces try to keep it back to the equilibrium.

For a chemical reaction at equilibrium, the analogy of pushing a side of the swing would be suppressing the production or decreasing the amount of a reactant product.
aA + bB ⇆ cC + dD
If we remove product “C” or “D” from the equilibrium mixture, the reaction will shift forward producing more of it to compensate for the loss. And the same would happen if we take out some of the reactant “A” or “B”; the reverse reaction will predominate till the equilibrium is reestablished.
Now, the question is why do we need/want to disturb the equilibrium?
Well, chemical synthesis is a production – we produce compounds that are needed for different applications and the main goal of this production is to maximize the conversion of reactants to products. For example, the Haber process for the synthesis of ammonia from hydrogen and nitrogen gases is carried out at very higher temperatures and pressure to shift the equilibrium towards the formation of ammonia.
3H2(g) + N2(g) ⇆ 2NH3(g)
These experimental conditions were adjusted over and over until the optimal yield of ammonia was achieved.
So, the next question is what experimental conditions can we adjust to achieve an equilibrium that favors our target products?
There are three main factors that can affect the composition of an equilibrium mixture:
- The concentration of reactants or products
- The pressure and volume
- The temperature
Let’s see how each of these factors affects the equilibrium of a chemical reaction.
Changing Concentrations at Equilibrium
- Adding a reactant produces more product by consuming some of the reactants.
- Adding a product produces more reactants by consuming some of the product.
For example, the equilibrium of the reaction between nitrogen and oxygen gases forming nitrogen monoxide can be shifted to the right by adding more reactants to the system. This happens because the system tends to reestablish the equilibrium by consuming the extra amounts of the reactants.
If nitrogen monoxide is added to the system, the equilibrium shifts to the left in order to consume some of it and re-establish the equilibrium.
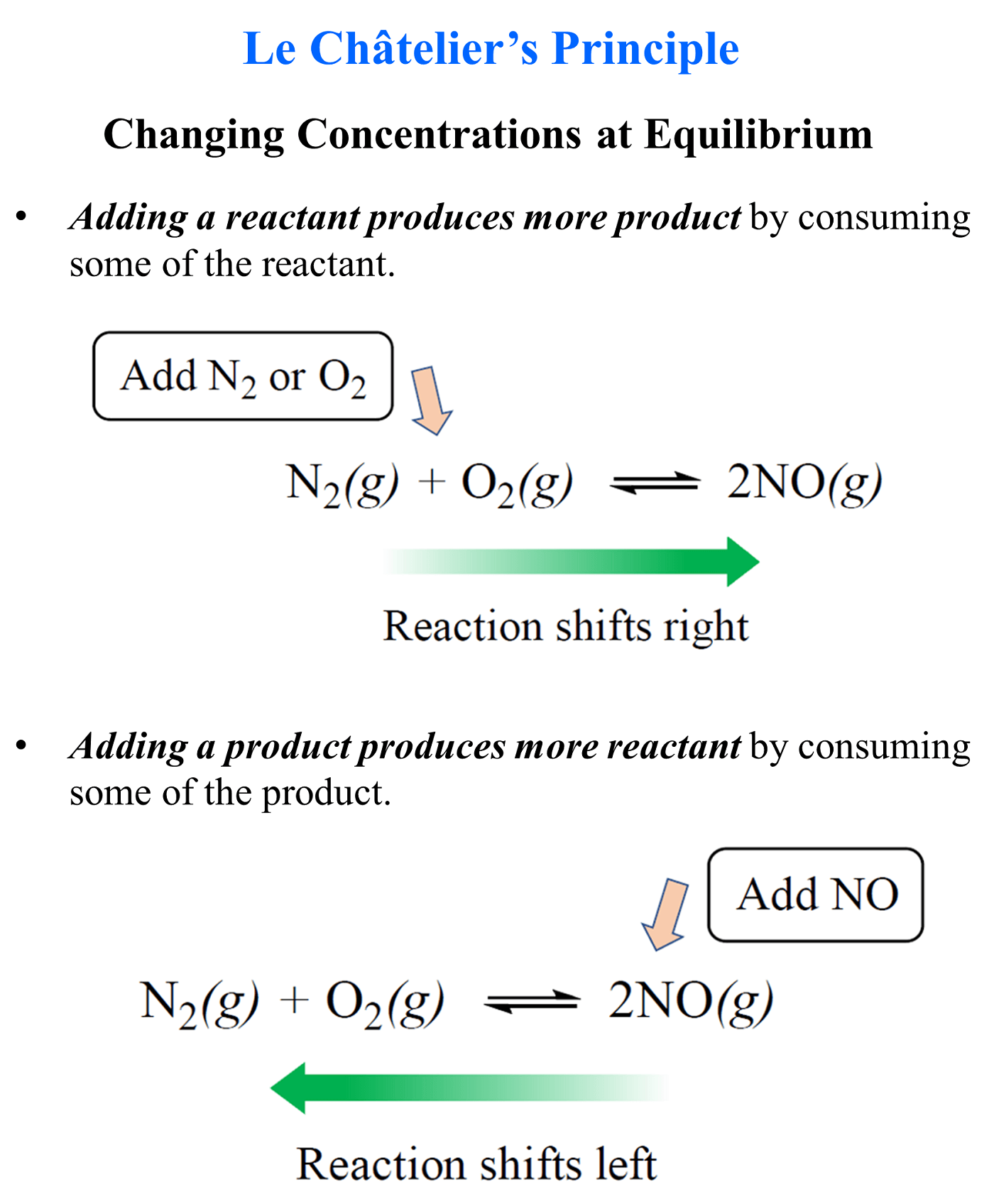
Now let’s see why this happens mathematically. Suppose at equilibrium there are 0.50 M N2, 0.40 M O2, and 1.6 M NO. The equilibrium constant, therefore, would be:
\[K\; = \,\frac{{{{[{\rm{NO}}]}^{\rm{2}}}}}{{[{{\rm{N}}_{\rm{2}}}][{{\rm{O}}_{\rm{2}}}]}}\, = \;\frac{{{{\left( {1.6} \right)}^2}}}{{\left( {0.50} \right)\left( {0.40} \right)}}\; = \,12.8\]
If we add 0.6 M O2, the concentrations are going to such that the equilibrium constant stays the same because it is a constant. Now, notice that the concentration of the oxygen appears in the denominator, and therefore, to keep the K constant at 12.8, some of the added oxygen must be consumed.
N2(g) + O2(g) ⇆ 2NO(g)
We can also see this by determining the reaction quotient before the equilibrium is established. The concentrations of the components at that point would be:
[NO] = 1.6 M, [O2] = 0.40 + 0.60 = 1.0 M, [N2] = 0.50 M
Therefore, the quotient is:
\[Q\; = \,\frac{{{{[{\rm{NO}}]}^{\rm{2}}}}}{{[{{\rm{N}}_{\rm{2}}}][{{\rm{O}}_{\rm{2}}}]}}\, = \;\frac{{{{\left( {1.6} \right)}^2}}}{{\left( {0.50} \right)\left( 1 \right)}}\; = \,5.12\]
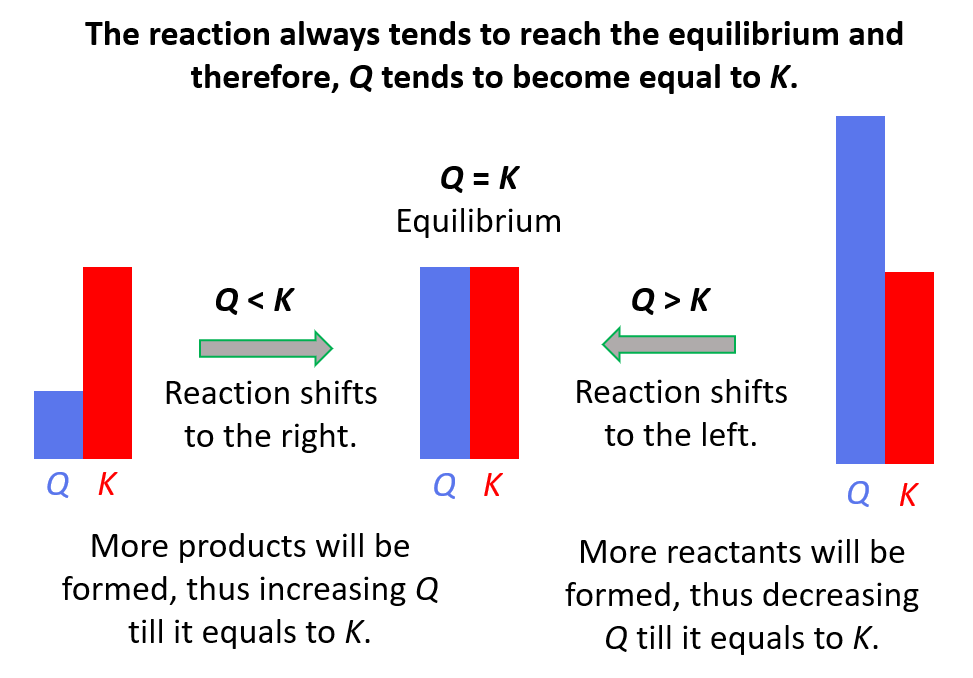
Notice that Q has decreased to a value less than K and we learned about the correlation between the K and Q, that the equilibrium is going to shift to the right to equalize Q and K.
Let’s determine the equilibrium concentrations of the components to confirm this mathematically. Assuming x M of the oxygen is consumed, the new concentrations at the equilibrium will be:
[NO] = 2x M, [O2] = 0.40 + 0.60 – x = (1.0 -x) M, [N2] = (0.50 – x) M
Refer to the principles of ICE tables if the expressions for determining the equilibrium concentrations are confusing to you.
The equilibrium constant is then equal to:
\[{K_{new}}\; = \,\frac{{{{[{\rm{NO}}]}^{\rm{2}}}}}{{[{{\rm{N}}_{\rm{2}}}][{{\rm{O}}_{\rm{2}}}]}}\, = \;\frac{{{{\left( {1.6\; + \;2x} \right)}^2}}}{{\left( {0.50\, – \;x} \right)\left( {1\, – \,x} \right)}}\; = \,12.8\]
Solving the equation, we find that x = 0.1586, and therefore, the equilibrium concentrations are:
[NO] = 1.9172 M, [O2] = 0.8414 M, [N2] = 0.3414 M
Let’s plug these numbers to make sure everything is correct:
\[{K_{new}}\; = \,\frac{{{{[{\rm{NO}}]}^{\rm{2}}}}}{{[{{\rm{N}}_{\rm{2}}}][{{\rm{O}}_{\rm{2}}}]}}\, = \;\frac{{{{\left( {1.6\; + \;2\, \times \,0.1586} \right)}^2}}}{{\left( {0.50\, – \;0.1586} \right)\left( {1\, – \,0.1586} \right)}}\; = \,12.79\,\]
The numbers are correct, and what we notice is that the concentrations of N2 and O2 (reactants) have decreased compared to what they were when 0.6 M O2 was added, while the concentration of NO (product) has increased:
N2: 0.5 vs 0.3414 M (decreased)
O2: 1 vs 0.8414 M (decreased)
NO: 1.6 vs 1.9172 M (increased)
And this confirms the statement about changing the concentration of components at equilibrium:
Adding a reactant produces more product by consuming some of the reactant.
Adding a product produces more reactant by consuming some of the product.
Changing The Reaction Volume
To understand the correlation between the volume and the equilibrium mixture, recall from the gases chapter that volume and pressure are inversely proportional (Boyle’s law). Therefore, decreasing volume will increase the pressure of the reaction mixture. According to Le Châtelier’s principle, the system will respond such that the pressure change is minimized.
So, how is the system going to bring the pressure back down?
Let’s consider the synthesis of ammonia:
3H2(g) + N2(g) ⇆ 2NH3(g)
What is important here is the coefficients of the gas molecules. Remember, they indicate the number of moles, and the greater they are, the higher the pressure. In other words, the more gas in the system, the higher the pressure. Therefore, if we increase the pressure by decreasing the volume, the system shifts to the right, decreasing the number of gas molecules and bringing the pressure back down.
So, in this case, decreasing the volume will shift the system to the right because there are only 2 moles of NH3 on the right vs a total of 4 moles of H2 and N2 on the left.
If we increase the reaction volume, the system will produce more gas molecules to compensate for the decrease in pressure. Therefore, increasing the volume of the reaction for ammonia synthesis will shift the equilibrium to the left because there are more gas molecules, and they compensate for the decrease in pressure.
You can also link the effect of volume change and the equilibrium this way; smaller volume – fewer molecules to fit in, larger volume – more molecules can fit in.
A good example to visualize this can be the conversion of a mole of N2O4 to two moles of NO2.
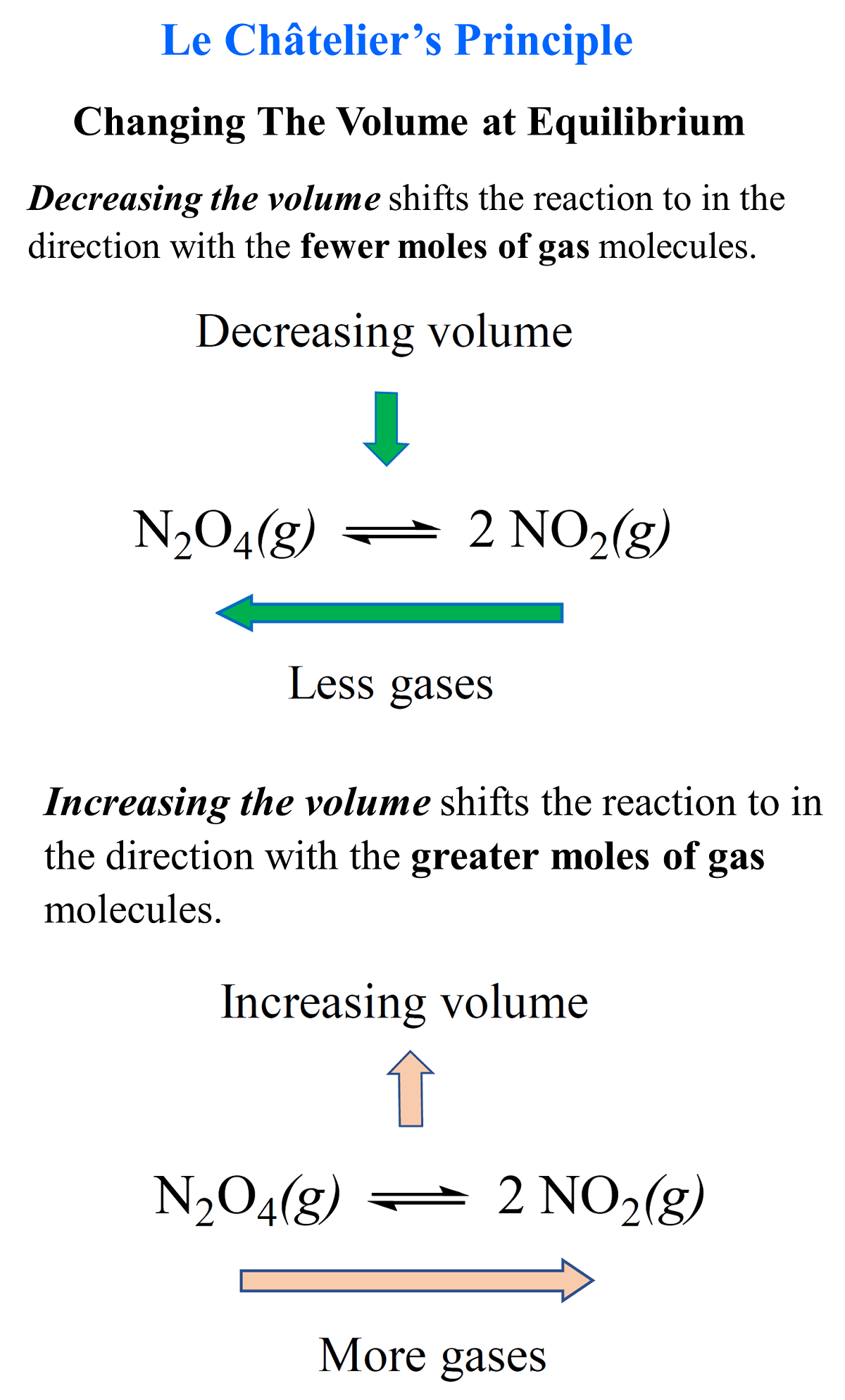
Summarizing the effect of volume on the equilibrium mixture, remember that:
Decreasing the volume shifts the reaction in the direction with the fewer moles of gas molecules.
Increasing the volume shifts the reaction in the direction with the greater moles of gas molecules.
If a reaction has an equal number of moles of gas on both sides of the chemical equation, then a change in volume has no effect on the equilibrium.
Changing The Pressure
The pressure can be changed in a few ways: 1) By decreasing the volume (see above), 2) By adding more substance to the mixture (see above), 3) By adding an inert gas.
We have seen how the change of pressure by changing the volume or the amount(s) of reaction components affects the equilibrium.
The third way of changing the pressure is by adding an inert gas such as, for example, argon.
Adding an inert gas does not cause a shift in equilibrium because it does not alter the partial pressures of any of the reacting components. Remember, when discussing the equilibrium constant, we mentioned that it was first formulated based on the partial pressures of gases (Kp). Therefore, if the partial pressures are not changed, then the equilibrium is not affected either.
Changing The Temperature
In the examples above when changing the concentration, volume, or pressure of the system, we used the terms equilibrium will shift, or the equilibrium will be changed. It is important to know that we were not talking about changing the value of the equilibrium constant as it only depends on the temperature. Instead, the composition of the equilibrium is changed. There may be an infinite number of possibilities for the concentrations of the components giving the same value of the equilibrium constant.
When concentration, pressure, or volume are changed, the composition of the equilibrium mixture changes because the reaction quotient Q no longer equals the equilibrium constant Kc. As a result, the system tries to compensate for the changes and equalize the quotient to the equilibrium constant.
The situation is different when the temperature is changed as it almost always affects the value of the equilibrium constant. The effect of temperature change on the equilibrium constant depends on whether it is a endothermic or an exothermic reaction.
To predict how the equilibrium constant and thus the direction of the reaction is changed, we treat the heat of the reaction as a product or reactant. If it is an exothermic reaction, heat is released so we treat it as a product. For endothermic reactions, the heat is absorbed, and therefore, we treat it as a reactant.
So, if we increase the temperature of an exothermic reaction, the equilibrium shifts to the left because heat is a product, and the system tries to consume some of the added heat.
So, if we increase the temperature of an endothermic reaction, the equilibrium shifts to the right because heat is a reactant, and the system tries to consume some of the added heat:

Keep in mind that the signs of enthalpy and what we write here as heat are different. For example, the enthalpy of an exothermic reaction is negative while we write it here “ + heat”.
Practice
Consider the following equilibrium process
2SO3(g) ⇆ 2SO2(g) + O2(g) ΔH° = 2198 kJ/mol
How will the concentrations of SO2, O2, and SO3 be affected in each scenario?
(a) the temperature is increased
(b) the pressure is decreased by increasing the volume of the container
(c) the concentration of O2 is increased
(d) a is added catalyst
(e) an inert gas is added at a constant volume
Suppose you need to increase the amount of C3H6Cl2 produced in the following exothermic reaction:
C3H6(g) + Cl2(g) ⇆ C3H6Cl2(g)
Which of the following strategies will work once the reaction mixture reaches equilibrium?
a) decreasing the reaction volume
b) removing C3H6Cl2 from the reaction mixture as it forms
c) adding a catalyst
d) adding Cl2
e) increasing the temperature
Predict the shift in the equilibrium position that will occur for each of the following reactions at equilibrium when the volume of the reaction container is increased.
1) PCl3(g) + Cl2(g) ⇆ PCl5(g)
2) 2NBr3(g) ⇆ N2(g) + 3Br2(g)
3) CO(g) + Cl2(g) ⇆ COCl2(g)
4) H2(g) + B2(g) ⇆ 2HBr(g)
5) MgCO3(s) ⇆ MgO(s) + CO2(g)
Consider the following equilibrium process for the commercial production of hydrogen:
CO(g) + H2O(g) ⇆ CO2(g) + H2(g) ΔH° = +42 kJ/mol
Predict the direction of the shift in equilibrium when
(a) the temperature is raised.
(b) more CO gas is added to the reaction mixture.
(c) some CO2 is removed from the mixture.
(d) the pressure on the gases is increased by changing the volume of the container.
(e) a catalyst is added to the reaction mixture
Consider this reaction at equilibrium:
N2 + O2(g) ⇆ 2NO(g)
Predict whether the reaction will shift left, shift right, or remain unchanged after each disturbance.
a) NO is added to the reaction mixture.
b) N2 is added to the reaction mixture.
c) NO is removed from the reaction mixture.
Check Also
- Chemical Equilibrium
- Equilibrium Constant
- Kpand Partial Pressure
- Kp and KcRelationship
- K Changes with Chemical Equation
- Equilibrium Constant K from Two Reactions
- Reaction Quotient – Q
- ICE Table – Calculating Equilibrium Concentrations
- ICE Table Practice Problems
- Le Châtelier’s principle
- Le Châtelier’s principle Practice Problems
- Chemical Equilibrium Practice Problems
