In the previous post, we talked about Heat Capacity and Specific Heat. The formula we use to calculate the heat transferred between the objects is given as:

 

 

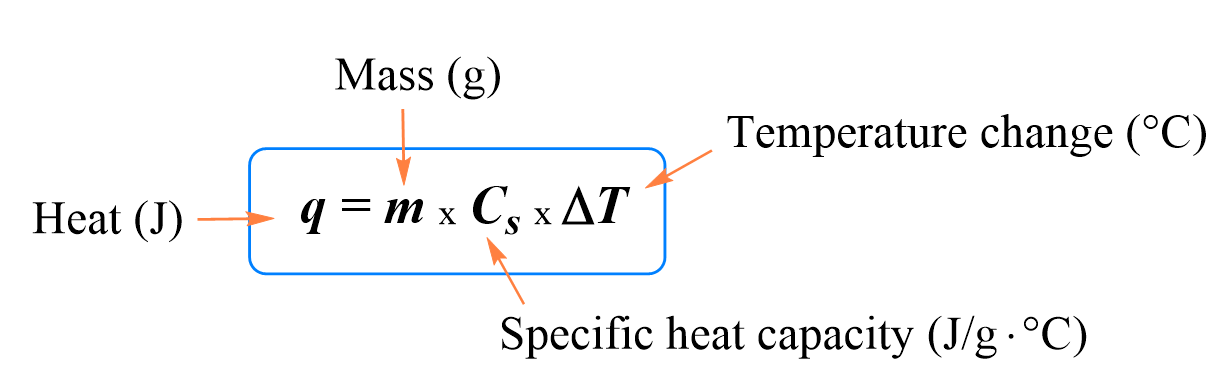
By using this formula, we were able to calculate, for example, how much heat was needed to raise the temperature of a metal, water, or any other object.

These calculations, however, were always conducted for the compound in the same phase – solid, liquid, or a gas, but not for phase transitions. So, how do we calculate the heat when there is a phase change?

For example, how many Joules of energy does it take to change 36.0 g of ice at -15.0 °C to liquid at 0. °C ? The specific heat of ice is 2.10 J/g°C and the heat of fusion (ΔH_fus) for ice is 334.0 J/g.

The provided heat is used to first raise the temperature of the ice to 0 ^oC, and then melt it: solid to liquid phase change. We can better visualize this using a graph:

 

 

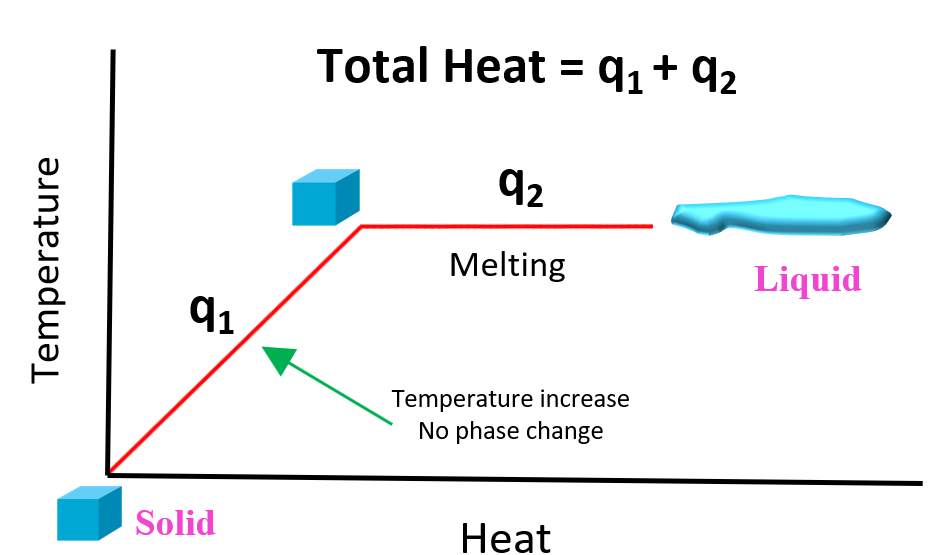
In the first segment of the graph, the temperature of the solid increases but there is no phase change (q₁). So, for this problem, it is the ice heating from -15.0 °C to liquid at 0. °C. After this, the heat (q₂) is consumed to melt the ice at 0 ^oC without increasing the temperature. Notice that the specific heat or the heat required to raise the temperature of 1 gram of the substance by 1 °C is different when it is a solid, liquid or a gas state. For the ice, the specific heat is 2.10 J/g°C, and for liquid water, it is described by heat of fusion (ΔH_fus) equal to 334.0 J/g.

The overall heat of this process then is:

q = q₁ + q₂

q = q_heating + q_melting

q_heating is calculated by the formula we have already used several times:

q_heating = m × C × ΔT

\[{{\rm{q}}_{{\rm{heating}}}}\;{\rm{ = }}\;{\rm{36}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{2.10\;{\rm{J}}}}{{\cancel{{\rm{g}}}\;\cancel{{^{\rm{o}}{\rm{C}}}}}}\;{\rm{ \times }}\;{\rm{(0}}\;{\rm{ – }}\;( – {\rm{15}}{\rm{.0)}}\;\cancel{{^{\rm{o}}{\rm{C}}}}\;{\rm{ = }}\;{\rm{1,134}}\;{\rm{J}}\]

To calculate the amount of energy required to melt the ice, we use the following formula:

q = mΔH_fus

\[{{\rm{q}}_{{\rm{melting}}}}\;{\rm{ = }}\;{\rm{36}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{334.0\;{\rm{J}}}}{{\cancel{{\rm{g}}}\;}}\;{\rm{ = }}\;{\rm{12,024}}\;{\rm{J}}\]

q = 1134 J + 12,024 J = 13,158 J

Rounding off to three significant figures, we have q = 1.32 x 10⁴ J or 13.2 kJ.

Following the same principle, we can draw an entire graph showing the heating and phase change for the solid-liquid-gas transition.

 

 

In the A-B region, there is no phase change, and it is only the increase of temperature for the substance in solid phase. The B-C region represents the melting where the temperature stays constant, and the heat absorbed by the substance is used to melt the solid to liquid. In the C-D region, the temperature of the liquid is increasing without a phase change, and from D to E region, we have the vaporization (evaporation) of the substance from liquid to gas state. The temperature of the substance in the gas state is increasing in the E-F segment.

Let’s consider an example where ice is transformed from solid to liquid at 42.0°C. How much energy, in kJ, is necessary to raise the temperature of 6.47 g of ice at -18.0°C to liquid at 42.0°C? The specific heat of ice is 2.10 J/g°C, the specific heat of water is 4.18 J/g°C, and ΔH_fus = 334.0 J/g.

This transition has one more step compared to the previous one and that is the heating of the liquid form 0 ^oC to 42.0 ^oC. So, the process starts from point A, or somewhere between A and B, and goes to a point between C and D.

The overall heat of this process then is:

q = q_{ice heating} + q_{ice melting} + q_{liquid heating}

For the ice heating, the initial temperature is -18.0 ^oC and the final temperature is 0.00 ^oC. For melting, there is no initial and final as it happens at 0 ^oC. For heating the liquid, the initial temperature is 0.00 ^oC and the final temperature is 42.0 ^oC.

\[{\rm{q}}\;{\rm{ = }}\,{\rm{6}}{\rm{.47}}\cancel{{\rm{g}}}\,{\rm{ \times }}\,{\rm{2}}{\rm{.10}}\,\frac{{\rm{J}}}{{\cancel{{\rm{g}}}\,\cancel{{^{\rm{o}}{\rm{C}}}}}}\,{\rm{ \times }}\,{\rm{(0}}{\rm{.00}}\,{\rm{ – }}\,{\rm{( – 18}}{\rm{.0))}}\,\cancel{{^{\rm{o}}{\rm{C}}}}\, + \,{\rm{6}}{\rm{.47}}\cancel{{\rm{g}}}\,{\rm{ \times }}\,{\rm{334}}{\rm{.0}}\,\frac{{\rm{J}}}{{\cancel{{\rm{g}}}\,}}{\rm{ + }}\,{\rm{6}}{\rm{.47}}\cancel{{\rm{g}}}\,{\rm{ \times }}\,{\rm{4}}{\rm{.18}}\,\frac{{\rm{J}}}{{\cancel{{\rm{g}}}\,\cancel{{^{\rm{o}}{\rm{C}}}}}}\,{\rm{ \times }}\,{\rm{(42}}{\rm{.0}}\,{\rm{ – }}\,{\rm{0}}{\rm{.00)}}\,\cancel{{^{\rm{o}}{\rm{C}}}}{\rm{ = }}\, – {\rm{3}}{\rm{.54}}\, \times \,{\rm{1}}{{\rm{0}}^{\rm{3}}}\,{\rm{J}}\]

 

Phase Changes from Gas State

In the examples above, we discussed the heat and phase change of water going from solid to gas state. Let’s now discuss the reverse process where the substance starts at a gas state. The key difference here is that the heat is released rather than absorbed by the compound/system. Initially, the gas loses some heat decreasing the temperature and some more heat is released when it condenses to a liquid state.

 

 

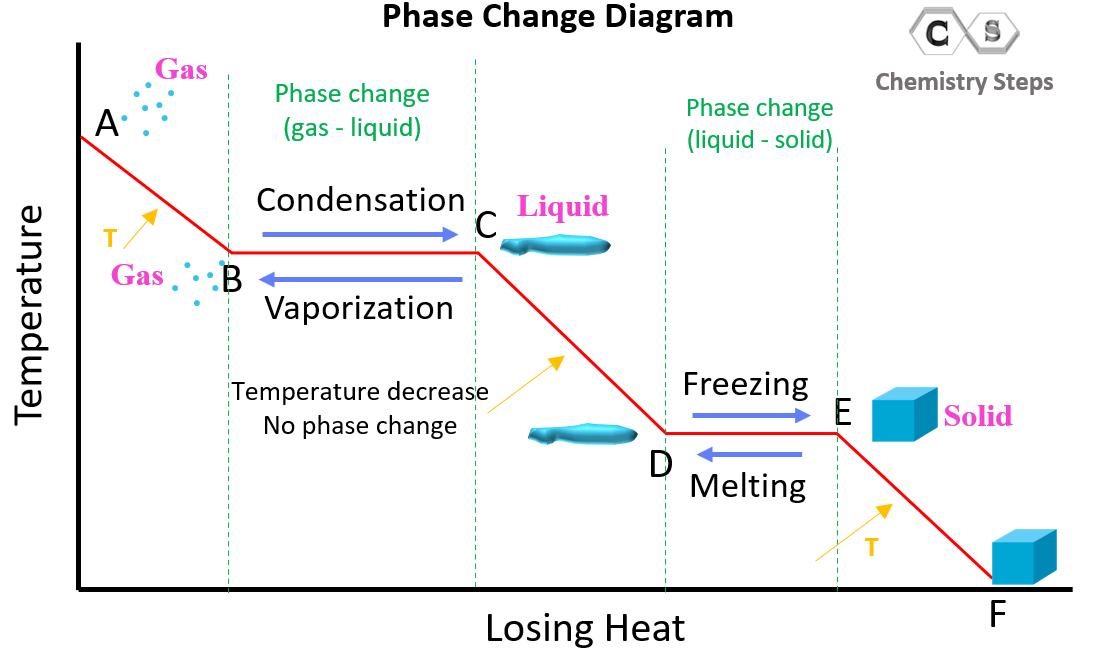
The graph starts from higher temperature which means the transition goes from the gas–liquid – solid direction. There are two phase changes (marked with green dotted lines). In the A-B region, there is no phase change, and it is only the decrease of temperature for the substance in the gaseous phase. The B-C region represents condensation where the temperature stays constant, and the heat lost by the substance is responsible for the solid-to-liquid transition. In the C-D region, the temperature of the liquid decreases without a phase change, and from D to E region, we have the freezing of the substance (liquid to solid state). The temperature of the substance in the solid state is decreasing in the E-F segment.

 

For example, how many joules of energy are associated with cooling 148 g of water from 46.0°C to ice at 0.00 °C? The specific heat of water is 4.18 J/g°C, and ΔH_fus = 334.0 J/g.

The substance goes from liquid to solid state, and we need to consider that some of the heat lost by water is responsible for freezing it. Recall the phase change graph.

So, it starts from C, or somewhere between C and D, and goes to E, and therefore, we need to add to q’s: (q_cooling and q_freezing). For the cooling, we use the specific heat of water (4.18 J/g°C), and for freezing we ΔH_fus (334.0 J/g) with opposite sign because fusing/melting and freezing are reverse processes.

q = q_heating + q_melting

q_heating is calculated by the formula we have already used several times:

q_heating = m × C × ΔT

q = q_cooling + q_freezing = m × C × ΔT + m × (-ΔH_fus)                

 

\[{\rm{q}}\;{\rm{ = }}\,{\rm{148}}\cancel{{\rm{g}}}\,{\rm{ \times }}\,{\rm{4}}{\rm{.18}}\,\frac{{\rm{J}}}{{\cancel{{\rm{g}}}\,\cancel{{^{\rm{o}}{\rm{C}}}}}}\,{\rm{ \times }}\,{\rm{(0}}{\rm{.00}}\;{\rm{ – }}\;{\rm{46}}{\rm{.0)}}\,\cancel{{^{\rm{o}}{\rm{C}}}}\, + \,{\rm{148}}\cancel{{\rm{g}}}\,{\rm{ \times }}\,( – {\rm{334}}{\rm{.0}}\,\frac{{\rm{J}}}{{\cancel{{\rm{g}}}\,}}{\rm{) = }}\, – {\rm{7}}{\rm{.79}}\, \times \,{\rm{1}}{{\rm{0}}^{\rm{4}}}\,{\rm{J}}\]

 

Check Also

• Energy Related to Heat and Work
• Endothermic and Exothermic Processes
• Heat Capacity and Specific Heat
• Heat Capacity Practice Problems
• What is Enthalpy
• Constant-Pressure Calorimetry
• Bomb calorimeter – Constant Volume Calorimetry
• Calorimetry Practice Problems
• Stoichiometry and Enthalpy of Chemical Reactions
• Hess’s Law and Enthalpy of Reaction
• Hess’s Law Practice Problems
• Standard Enthalpies of Formation
• Enthalpy of Reaction from Enthalpies of Formation
• Thermochemistry Practice Problems
• Thermochemistry Quiz