In this set of practice questions, we will go over the main types of questions on calorimetry including the heat capacity, the heat of reaction, finding the final temperature of a mixture, constant pressure calorimetry, and constant-volume calorimetry.
A few important concepts and formulas you will need to solve these questions.
Heat capacity and specific heat are correlated by the following formula:
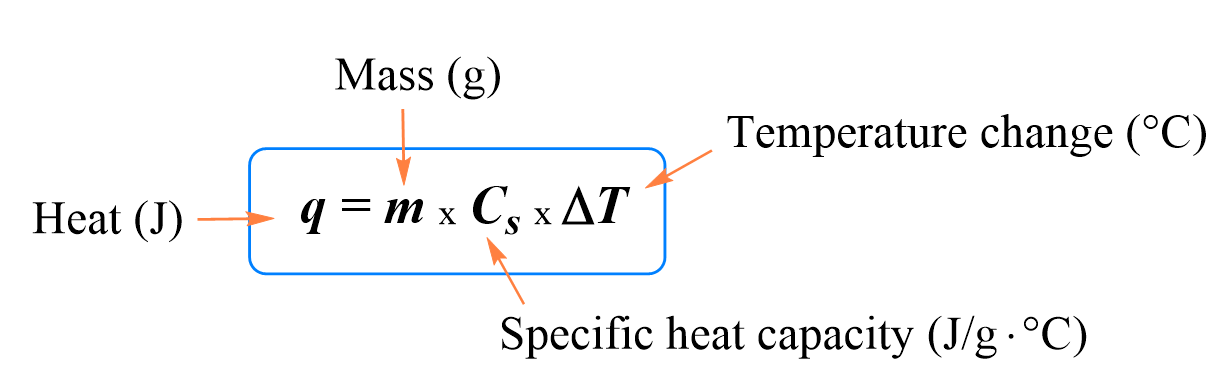
When solving a problem related to heat capacity and heat transfer, remember that most of the time, it is assumed the heat is not lost, and it only flows from the object with a higher temperature to the colder one:

The heat transfer to/from the calorimeter is determined by its temperature change and the heat capacity:
qcal = Ccal x ΔT
The heat capacity of the calorimeter is determined experimentally and is already known when measuring the heat/enthalpy of a reaction.
Remember, the enthalpy change (ΔH) is equal to the heat when the pressure is constant:
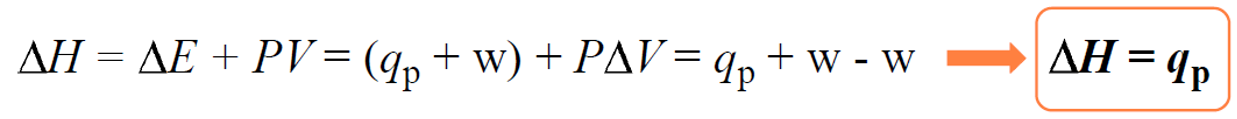
On the other hand, a bomb calorimeter is an equipment that measures ΔE for combustion reactions. This can be seen in the equation of internal energy change:
ΔE = q + w
w = PΔV and ΔV is zero when the volume is constant. So, for a constant volume, ΔE = q, and therefore, the bomb calorimeter measures the energy change of a chemical reaction.
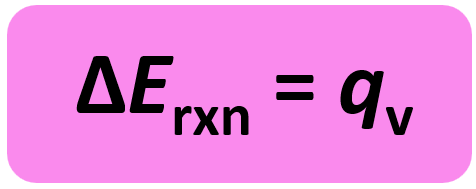
The experiment is carried out in an insulated sealed vessel called a bomb which is designed to withstand high pressures. The bomb is placed in a water container and by measuring its temperature change caused by the reaction, we determine the heat of the calorimeter.
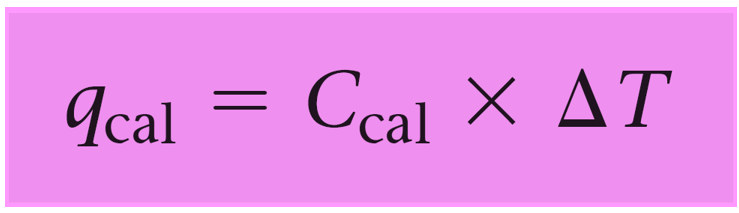
The links to the corresponding topics are given below:
1.
How much heat in kJ is required to warm 1.50 L of water from 25.0 oC to 100.0 °C? (Assume a density of 1.0 g/mL for the water.)
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
2.
What is the final temperature when a 40 g sample of water at 90 °C is mixed with a 60 g sample at 25 °C?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
3.
How much heat does it take to increase the temperature of a 540.6-g sample of Fe from 20.0 °C to 84.3 °C? The specific heat of iron = 0.450 J/g °C.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
4.
Calculate the specific heat capacity of a metal if a 17.0 g sample requires 481 J to change the temperature of the metal from 25.0 °C to 67.0 °C?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
5.
Calculate the energy of combustion for one mole of butane if burning a 0.367 g sample of butane (C4H10) has increased the temperature of a bomb calorimeter by 7.73 °C. The heat capacity of the bomb calorimeter is 2.36 kJ/ °C.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
6.
How many joules of energy is required to melt 40.0 g of ice at 0 °C? The heat of fusion (ΔHfus) for ice is 334.0 J/g.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
7.
How many kJ of energy does it take to change 36.0 g of ice at -15.0 °C to water at 0. °C ? The specific heat of ice is 2.10 J/g°C and the heat of fusion (ΔHfus) for ice is 334.0 J/g. Ignore the significant figures for this problem.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
8.
The enthalpy change for the reaction is given below:
2CH3OH(l) + 3O2(g) → 4H2O(l) + 2CO2(g) ΔH = -1452.8 kJ
a) What quantity of heat is released for each mole of water formed?
b) What quantity of heat is released for each mole of oxygen reacted?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
9.
How much heat will be released if 44.8 g of SO2 is reacted with an excess of oxygen according to the following chemical equation?
2SO2(g) + O2(g) → 2SO3(g), ΔH° = –198 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
10.
What is ΔH° for the following reaction
2C6H6(l) + 15O2(g) → 12CO2(g) + 6H2O(l), ΔH° = ? kJ
if the consumption of 27.3 g of benzene (C6H6) produces 1144 kJ of heat?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
11.
Based on the heat of reaction for the chlorination of methane, how much heat will be released if 233.6 grams of hydrochloric acid are formed?
CH4(g) + 3Cl2(g) → CHCl3(l) + 3HCl(g), ΔH° = -334 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
12.
Calculate how many kJ of heat-energy will be released when 12.65 g of magnesium carbonate reacts with 650. mL of 0.400 M hydrochloric acid?
MgCO3(s) + 2HCl(aq) → MgCl2(aq) + H2O(l) + CO2(g), ΔH° = –112 kJ
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.


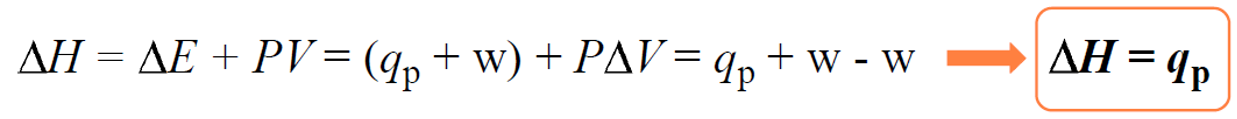
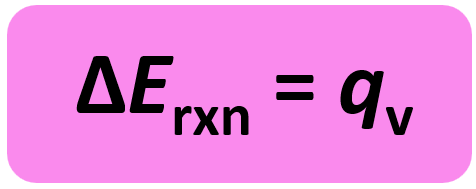
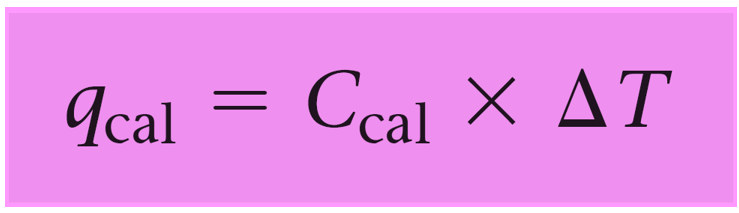

This was so helpful,thank you so much!
Glad to hear that, Chirambo.