The titration curve for Polyprotic Acids

General Chemistry

In the previous few posts, we have been discussing acid-base titrations involving pH calculations and analyzing the titrations curves.

A typical acid-base titration curve can be obtained, for example, based on the reaction of HCl and NaOH:

 

 

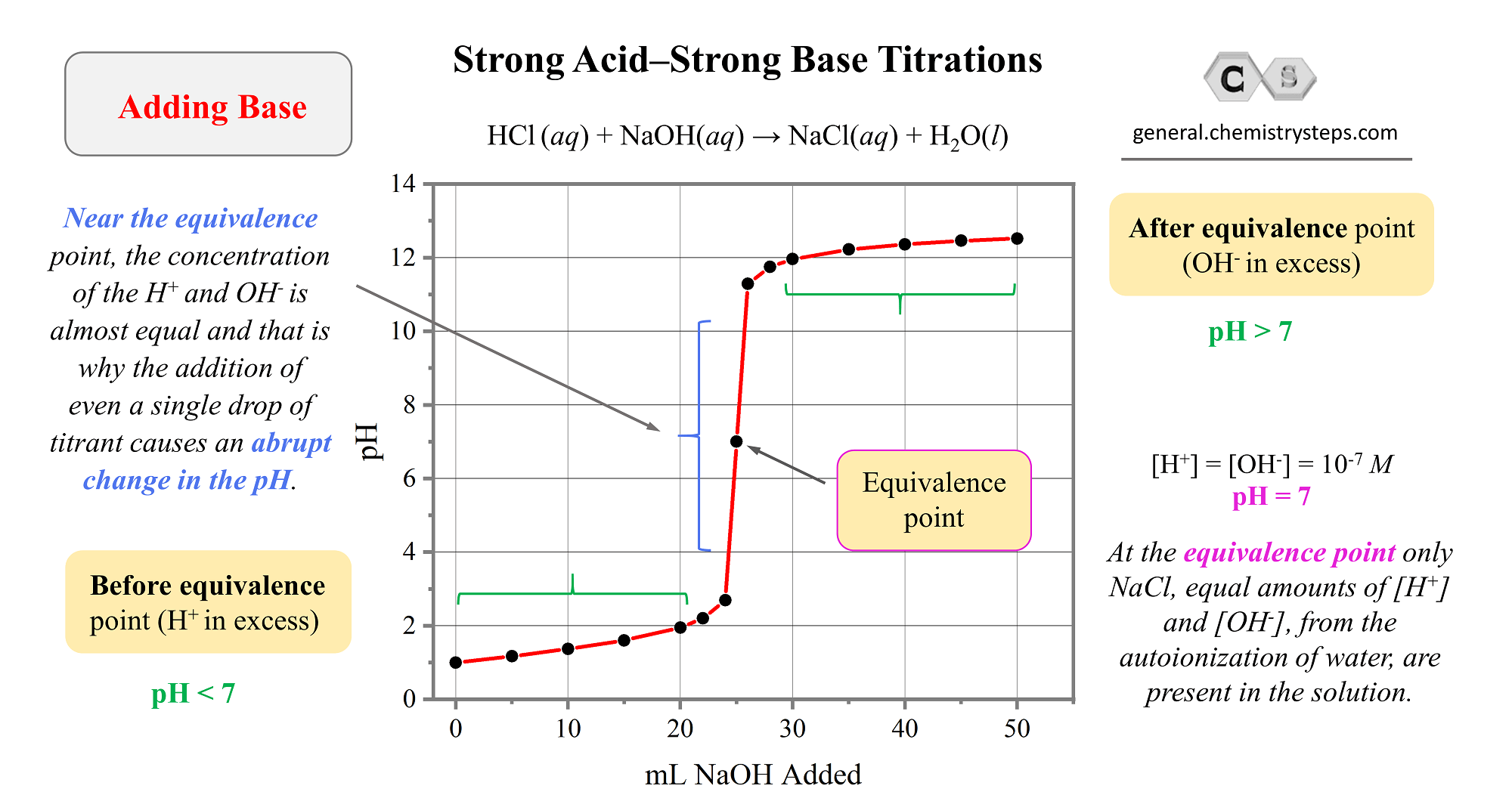
Check the original article for more details and explanations, and once the concepts are clear, let’s discuss the titration of a polyprotic acid.

For example, H2SO3 is a diprotic acid, and its dissociation can be divides in two parts each associated with a different dissociation constant:

 

H2SO3(aq) + H2O(l) ⇆ HSO3–(aq) + H3O+(aq) Ka1 = 1.6 x 10-2

HSO3–(aq) + H2O(l) ⇆ SO32-(aq) + H3O+(aq) Ka2 = 6.4 x 10-8

 

When titrated with a base, one of the protons reacts with the hydroxide first to form the conjugate base HSO3–, which then reacts with the base forming the SO32- conjugate base.

Let’s say we are titrating 25.0 mL of 0.100 M H2SO3 with 0.100 M NaOH. The first part of the titration represents the reaction between H2SO3 and NaOH, and the second part is for the reaction between the conjugate base HSO3– and NaOH.

 

H2SO3(aq) + OH–(aq) ⇆ HSO3–(aq) + H2O(l)

HSO3–(aq) + OH–(aq) ⇆ SO32–(aq) + H2O(l)

 

The reason for the subsequent reaction with NaOH is that H2SO3 is a much stronger acid than its conjugate base HSO3– as seen from the Ka values.

So, the shape of the titration curve is going to be like merging two separate ones for monoprotic acids :

 

 

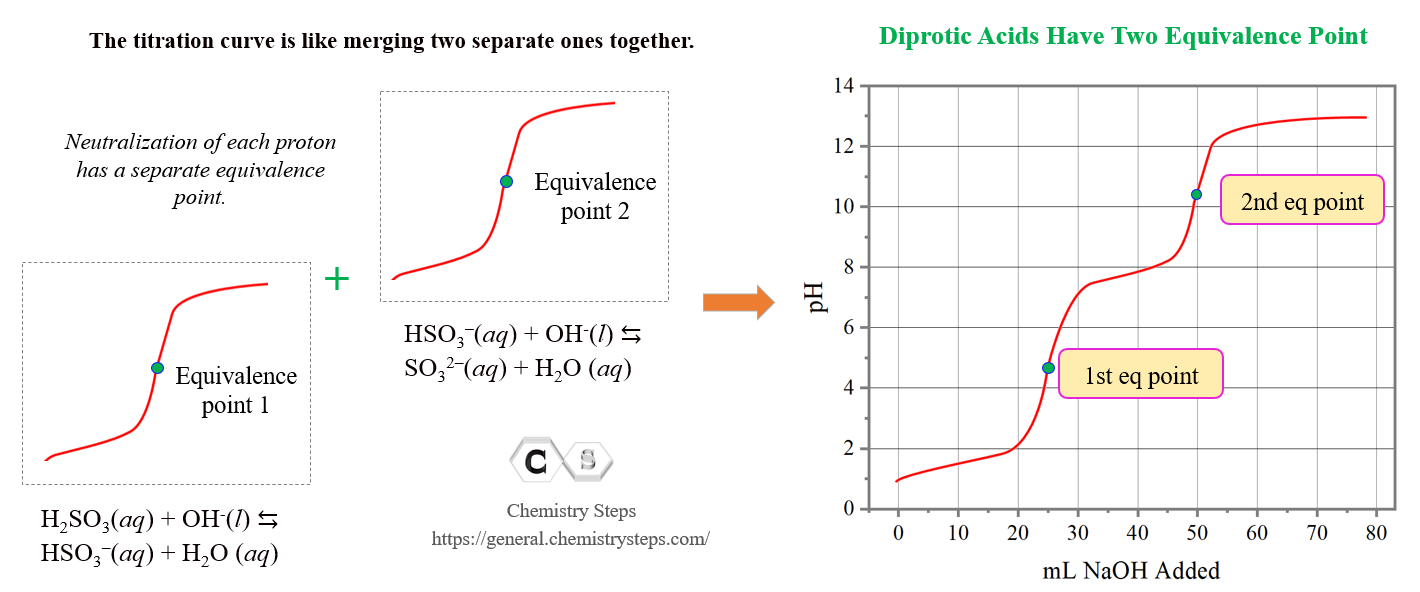
The pH before starting the titration is low because there is only acid present in the solution. H2SO3 is a weak acid and to calculate the pH, we follow the steps discussed earlier in the acid-base chapter. As the base is added, the pH increases, and up until the first equivalence point, we have a buffer solution composed of the H2SO3/HSO3– system.

 

 

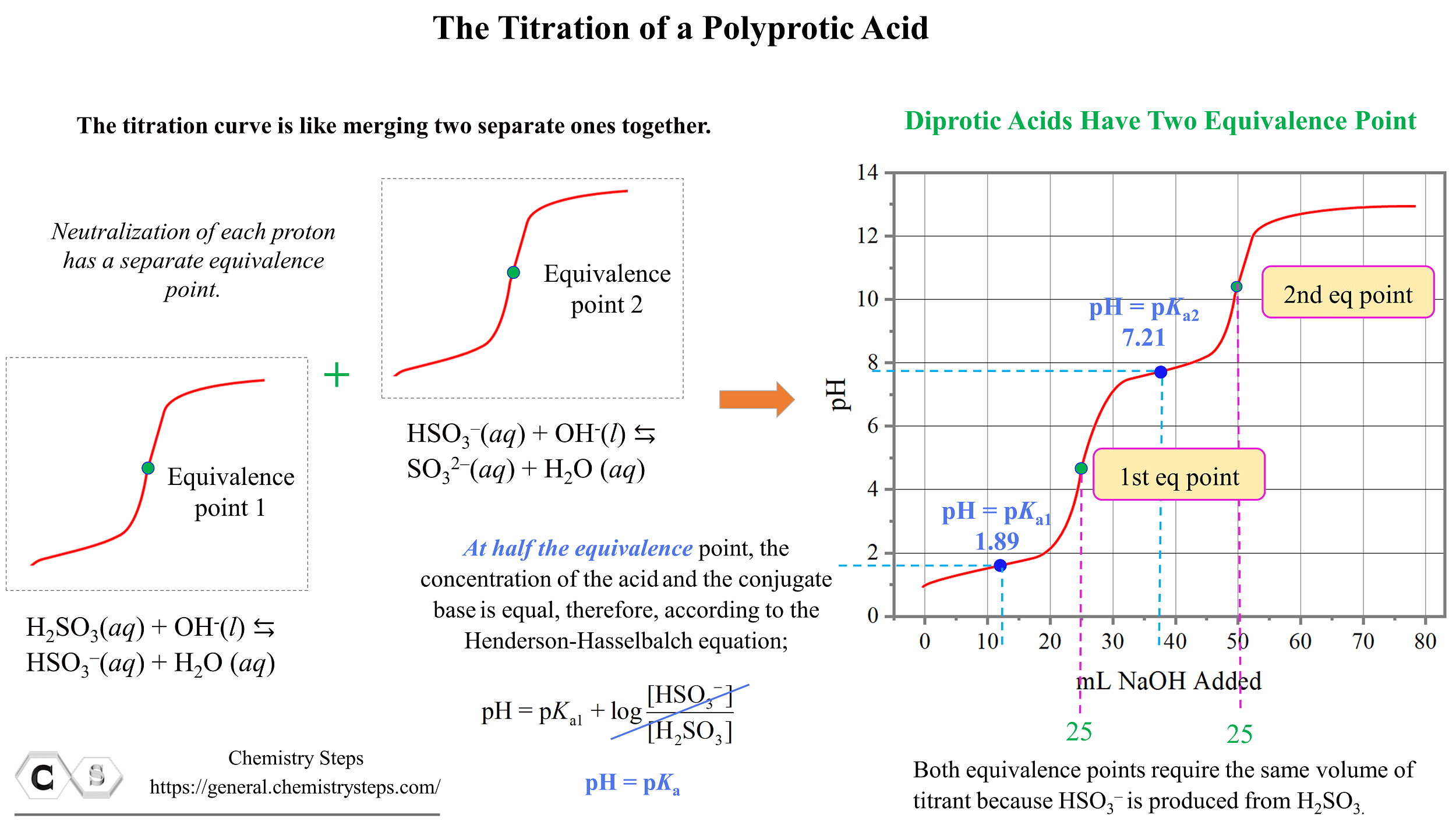
The pH at the first half equivalence point is equal to the pKa of sulfurous acid. Remember, this is because the pH of buffer solutions, when [HA] = [A–] becomes equal to the pKa since the logarithm term becomes zero.

 

\[{\rm{pH}}\;{\rm{ = }}\;{\rm{p}}{K_{{\rm{a1}}}}\;{\rm{ + }}\;\cancel{{{\rm{log}}\frac{{{\rm{[HS}}{{\rm{O}}_{\rm{3}}}^{\rm{–}}{\rm{]}}}}{{{\rm{[}}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{3}}}{\rm{]}}}}}}\; = \,{\rm{p}}{K_{{\rm{a1}}}}\]

 

At the first equivalence point, pH is below 7 because of the acidic nature of HSO3–.

The pH at the second half equivalence point corresponds to the pKa of the conjugate base HSO3–. Notice that for both equivalence points, the same volume of the NaOH (25.0 mL) is needed because the HSO3– is produced from H2SO3 in a 1:1 mole-ratio.

The information from titration curves, and especially the correlation between the half equivalence point and the pH can be used to estimate the pKa values for the polyprotic acid and identify an unknown acid.

These should be the key points about the titration of polyprotic acids. Check the previous posts on titrations for more information and calculations:

 

 

Check Also

Leave a Comment