Standard enthalpy of formation (or heat of formation), ΔH^o_f , is the enthalpy change when 1 mol of the substance is formed from its constituent elements in their standard states.

For example, the formation of 1 mol ammonia from H₂ and N₂ gases releases 46.0 kJ heat:

1.5H₂(g) + 0.5N₂(g) ⇆ NH₃(g) ΔH^o_f = 46.0 kJ

A reminder about the standard states; depending on the topic, standard states are defined as follows:

• Gases: It is the pure gas at a pressure of exactly 1 atm.
• Liquids and Solids: It is the pure substance in its most stable form at a pressure of 1 atm and at the temperature of interest (usually at 25 ^oC).
• A Substance in Solution: It is when the concentration is exactly 1 M.

Let’s answer one question before moving on.

Why do we not talk about the enthalpy of a compound? Why enthalpy of formation of CO₂ and not enthalpy of CO₂?

Well, the problem is it is impossible to measure the absolute value of the enthalpy of a substance. So, what we do, is take a reference point like the sea level for the height of mountains, and measure the enthalpy change when a given compound or a substance is formed from its elements.

This reference point is the standard enthalpy of formation of any element in its most stable form which is set to zero.

For example, the standard enthalpy of formation for O₂ is zero, and that of Na, C (graphite), Br₂, etc. is zero.

Why did we mention graphite for carbon? Remember, carbon has a few allotropes, and the most common ones are graphite and diamond. Graphite is the most stable (standard state) of carbon and therefore, its enthalpy of formation is zero (), while that of diamond is not. Diamond is less stable and its conversion to graphite is an exothermic (downhill – thermodynamically favorable) process:

C(diamond) → C(graphite) ΔH° = – 1.9 kJ/mol

Fortunately, this process does not happen overnight, and we get to keep our diamonds.

Going back to the enthalpy of formation. So, imagine the elements in their standard form are lined up on the sea level (ΔH °_f = 0). Now, when a compound is formed by combining any elements, there is an enthalpy change which is the standard enthalpy of formation for that compound:

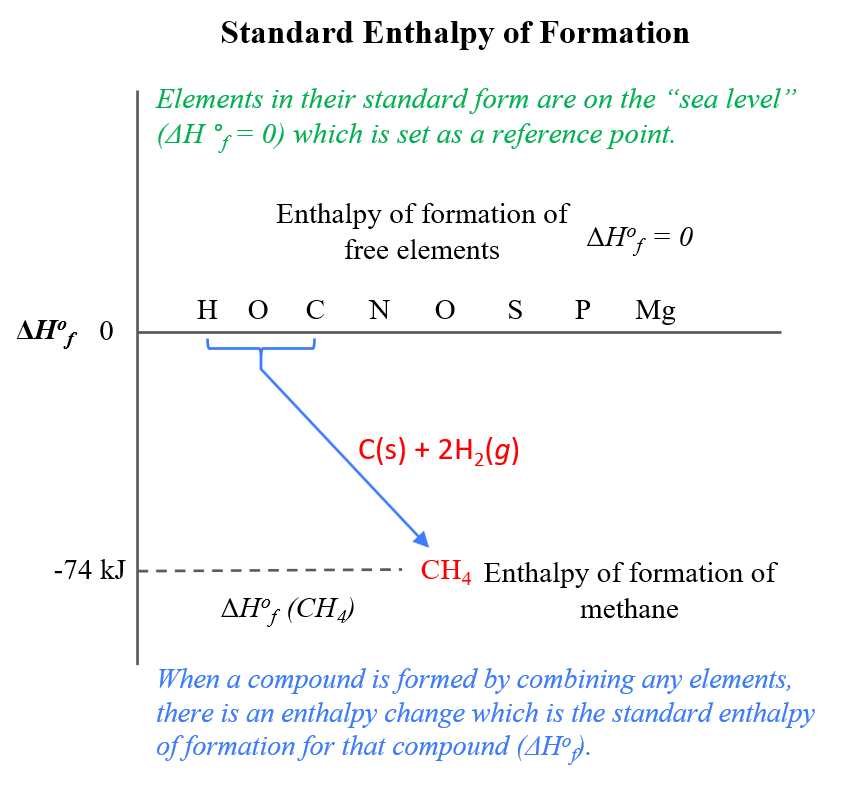
For example, the standard enthalpy of formation for methane from carbon, and hydrogen is -74.6 kJ/mol:

C(graphite) + 2H₂(g) → CH₄(g) ΔH °_f = -74.6 kJ/mol

The comprehensive list of the heat of formation can be found in your textbook or by a quick google search.

How do We use the Enthalpies of Formation?

There are countless reactions that can be carried out and it is not always that we can or need to measure their enthalpy change. However, by having a library of values for the enthalpies of formations, we can determine the enthalpy of a given reaction. There are two approaches to doing this.

1) The Direct Approach

If the enthalpies of formations for all the components of ac chemical reaction are known, then the following formula is used to determine the enthalpy of this reaction:

We will discuss this approach in the next post called “Enthalpy of Reaction from Enthalpies of Formation”.

2) The Indirect Approach

If the enthalpies of formation of all the components in chemical reactions are not known, then Hess’s law is used. You can go to the link for detailed coverage of the Hess’s law, but let’s use it here to address one more question you may be wondering about:

How is Enthalpy of Formation Measured?

We talked about the enthalpy of formation and, as an example, showed that the enthalpy of formation of methane is -74 kJ/mol, but how do we measure this?

C(graphite) + 2H₂(g) → CH₄(g) ΔH °_f = -74.6 kJ/mol

When we say the “reaction” forming a substance from its constituent elements, it is, very often, a hypothetical reaction. We can’t combine carbon and hydrogen in the laboratory to make methane. So, to determine its enthalpy of formation, we measure the enthalpy of the combustion reaction of methane using bomb calorimetry and then, apply the Hess’s law to obtain the ΔH °_f of methane.

The combustion reaction of methane is the sum of three reactions of formations of methane, CO₂, and H₂O:

C(s) + O₂(g) → CO₂(g) ΔH °_f (CO₂) = -393 kJ

+

2H₂(g) + O₂(g) → 2H₂O(l) ΔH °_f (H₂O) = -572 kJ

+

C(graphite) + 2H₂(g) → CH₄(g) –ΔH °_f (CH₄) = ?

____________________________________________

CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l) ΔH ° = -891 kJ

Notice that there is a negatice sign in from of ΔH °_f (CH₄) becasue the reaction is reversed.

Therefore, 

ΔH ° = ΔH °_f (CO₂) + ΔH °_f (H₂O) + (–ΔH °_f (CH₄)) = -891 kJ

Solving for ΔH °_f (CH₄), we get:

ΔH °_f (CH₄) = ΔH °_f (CO₂) + ΔH °_f (H₂O) + 891

ΔH °_f (CH₄) = -393 – 572 + 891 = -74 kJ/mol

Check Also

• Energy Related to Heat and Work
• Endothermic and Exothermic Processes
• Heat Capacity and Specific Heat
• Heat Capacity Practice Problems
• What is Enthalpy
• Constant-Pressure Calorimetry
• Bomb calorimeter – Constant Volume Calorimetry
• Stoichiometry and Enthalpy of Chemical Reactions
• Hess’s Law and Enthalpy of Reaction
• Hess’s Law Practice Problems
• Enthalpy of Reaction from Enthalpies of Formation
• Thermochemistry Practice Problems