To determine if SF4 i spolar or not, we need to first draw its Lewis structure and determine the geometry. We came up with the following Lewis structure in the previous post, so feel free to check it:
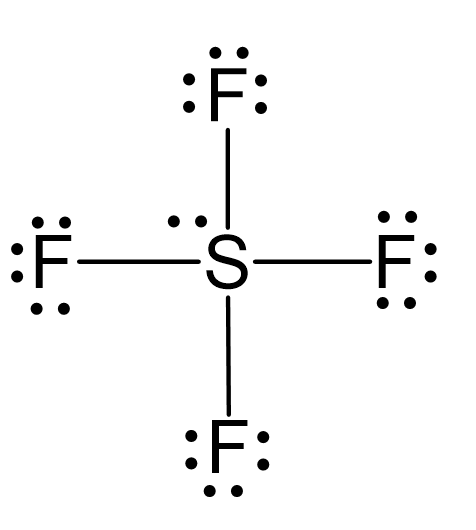
The central atom has 4 atoms connected to it, and one lone pair, therefore, the electron geometry is trigonal bipyramidal while the molecular geometry is seesaw:
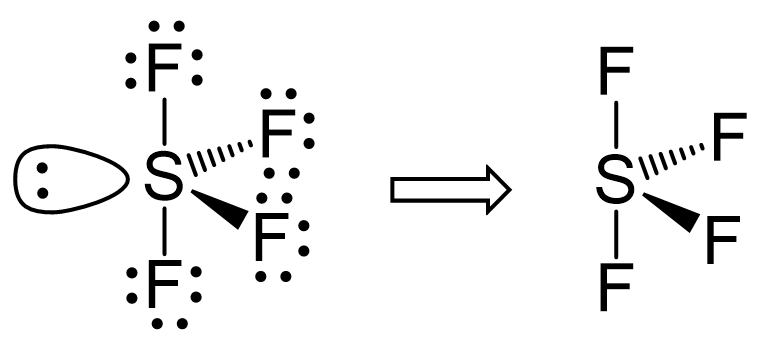

Now, the polarity: The first thing here is to determine if the S-F bond is polar. Depending on the difference in the electronegativity values, covalent bonds can be polar and nonpolar.

- If the difference in electronegativity is less than 0.5, the electrons are about equally shared between the two atoms, forming a nonpolar a covalent bond.
- If the difference in electronegativity is between 0.5 and 1.7, we have a polar covalent bond.
- A difference of 1.7 or higher is so large that the electrons are no longer shared, and an ionic bond is formed. Ionic bonds are formed between metals and nonmetals.
The difference in electronegativities is 1.5, and therefore, the S-F bond is polar and has a dipole. So, there are four dipoles in SF4:
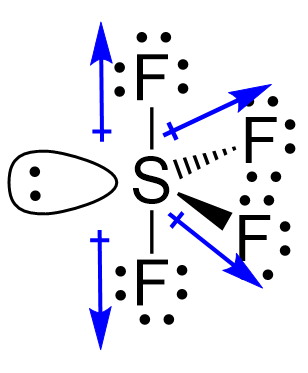
Now, whether the molecule is polar or not will depend on the orientation of all the dipoles. Remember, the molecule is polar if it has a dipole moment, and the molecular dipole is the vector sum of all the dipoles. The two dipoles on the left cancel each other, but the two on the right will add up to a molecular dipole pointing to the right as drawn:
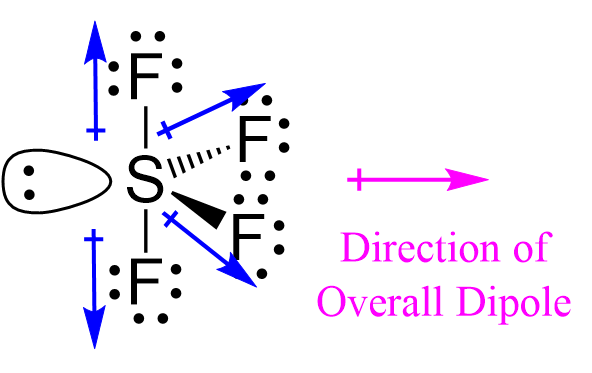
To summarize, we conclude that SF4 has a molecular dipole thus it is a polar molecule.
Check this 99-question multiple-choice quiz on Geometry and Hybridization:
Check Also
- The VSEPR Model
- VSEPR Theory Practice Problems
- Hybridization of Atomic Orbitals
- sp, sp2, sp3, sp3d, and sp3d2 Hybridization Practice Problems

