The first law of thermodynamics is the law of energy conservation, which states that energy can be converted from one form to another, but cannot be created or destroyed.
One implication of this law is that the total energy of the universe is constant. The energy transfers from a system to its surroundings but it is never lost.
The system is what we are interested in, while everything else is the surroundings.
The next question is how does the energy transfer take place? There are two ways the energy transfers between the system and surroundings; heat (q) and work (w).

So, energy is the capability of doing work or producing heat. Anytime the system does work or gives off heat, its energy decreases, and therefore, the q and w have negative signs. On the contrary, when work is done on the system or it absorbs heat, its internal energy increases (+q, +w).

Think of the internal energy as a bank account, it increases when work is done on it, and it decreases if a work is done by it.
For example,
A gas absorbs 62 kJ of heat and does 48 kJ of work. Calculate ΔE.
The internal energy change is equal to:
ΔE = q + w
If the heat is absorbed by the system, then it has a positive sign. The job done by the system indicates a negative sign for w.
ΔE = +62 kJ – 48 kJ = 16 kJ
Work and Energy
Work can be defined as force F multiplied by distance d: w = F x d
Although work has a very broad definition covering many aspects of thermodynamics, in this section, we study the work done by a gas that expands by moving the weightless cylinder of a piston.
Perhaps the best example here is the combustion of gasoline. The products CO2 and H2O gases expand the volume and thus move the piston which is the work done by the reaction.
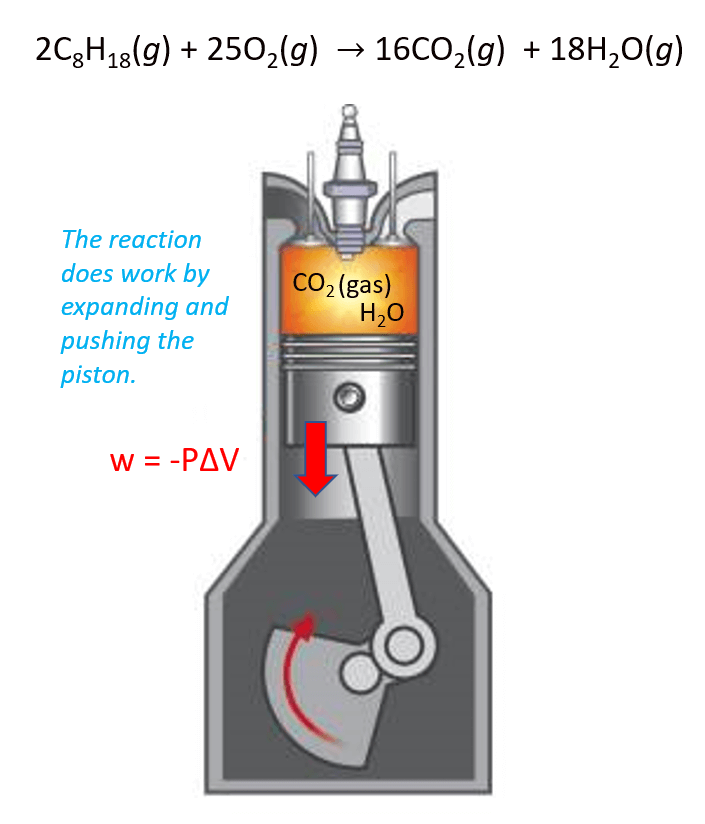
In this case, the work is calculated by the following formula:
w = –PΔV
where P is the pressure exerted by the gas, and ΔV is its volume change.
Example:
A pump is held under 1.30 atm external pressure. How much work (in J) is required to expand its volume from 1.80 L to 3.50 L?
W = -PΔV
W = -1.30 atm (3.50 L – 1.80 L) = -2.21 atm · L
The last step is to convert atm · L to Joules. 1 L· atm = 101.3 J, therefore:
\[{\rm{w}}\;{\rm{ = }}\;{\rm{ – 2}}{\rm{.21 }}\cancel{{{\rm{atm}}\;{\rm{\cdot}}\;{\rm{L}}}}\;{\rm{ \times }}\;\frac{{{\rm{101}}{\rm{.3 J}}}}{{{\rm{1}}\;\cancel{{{\rm{atm}}\;{\rm{\cdot}}\;{\rm{L}}}}}}\;{\rm{ = }}\;{\rm{224}}\;{\rm{J}}\;\]
Energy Change in Chemical Reactions
In chemistry, the system is the reaction and all the changes in energy are always looked at from the perspective of the system/reaction.
For example, the system can be a flask where the reaction takes place, or it can just be the reaction while the solvent in which the reactants and products are dissolved is already part of the surroundings.
A chemical reaction that gives off heat to its surroundings is called an exothermic reaction (negative q).
Endothermic reactions (endo means “within,” so heat flows in), on the other hand, absorb heat from surroundings, and q, in this case, is positive.
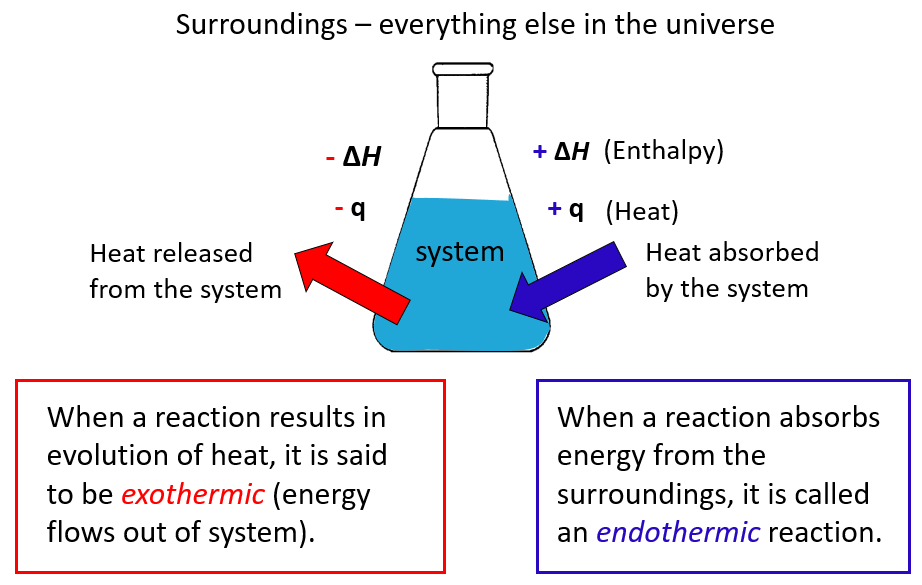
ΔH is the enthalpy change of the reaction and will cover it separately, however, for now, take it as if it is the heat since most often it is.
The energy change of chemical reactions can be calculated using calorimetry, and heats for formations by a direct method or using the Hess’s law. The links to the corresponding topics are shown below.
Practice
What is the ΔE of the system which does 42.0 kJ of work on the surroundings and absorbs 51.0 kJ of heat?
Calculate ΔE for each of the following.
a) q = -62 kJ, w = +59 kJ
b) q = +48 kJ, w = –56 kJ
c) q = -92 kJ, w = 0 kJ
The gas in a piston is heated up by absorbing 984 J of heat and expands performing 541 J of work on the surroundings.
What is the change in internal energy for the system (the gas)?
Calculate the change in internal energy of the system if it releases 415 kJ of heat and does 562 kJ of work on the surroundings.
A balloon filled with 8.50 moles of nitrogen at 23.0 oC expands from 3.54 L to 5.64 L by increasing its temperature to 58.0 oC under constant pressure of 1.10 atm. Calculate q, w, and ΔE in kJ for the nitrogen gas in the balloon if its heat capacity is 29.15 J/°C · mol.
Check Also
- Endothermic and Exothermic Processes
- Heat Capacity and Specific Heat
- Heat Capacity Practice Problems
- What is Enthalpy
- Constant-Pressure Calorimetry
- Bomb calorimeter – Constant Volume Calorimetry
- Stoichiometry and Enthalpy of Chemical Reactions
- Hess’s Law and Enthalpy of Reaction
- Hess’s Law Practice Problems
- Standard Enthalpies of Formation
- Enthalpy of Reaction from Enthalpies of Formation
- Thermochemistry Practice Problems
