In the previous post, we discussed the energy of nuclear reactions and the key point we learned was that nuclear reactions are associated with enormous amounts of energy because of the mass difference between the reactants and products.

For example, we calculated the mass difference in the combustion of methane to be 9.9 x 10^-9 g, which corresponds to 890.4 kJ/mol energy according to the Einstein’s E = mc² equation:

 

CH₄ + 2O₂ → CO₂ + 2H₂O, Δm = – 9.9 x 10^-9 g, ΔH = –890.4 kJ

 

As a comparison, the alpha decay of one mol of ²³⁸₉₂U isotope produces ²³⁴₉₀Th as a result of 0.0046 g mass decrease which is equivalent to -4.14 x 10⁸ kJ energy:

 

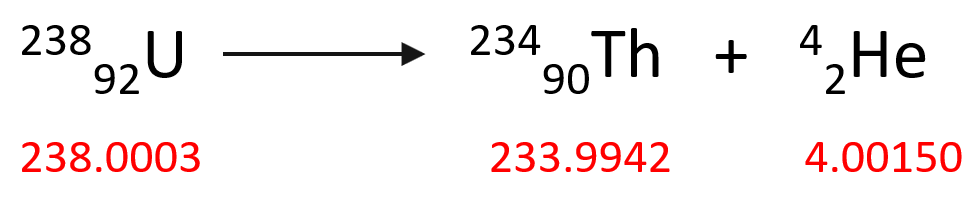
Δm = – 0.0046 g, ΔH = -4.14 x 10⁸ kJ

 

In the basis of the energy release and the difference between that of chemical and nuclear reactions is that mass interconverts into energy and vice versa. If the reaction is associated with loss of mass, then it will release energy equivalent to the that mass change. If the reaction, or the system, gains mass, then there must be an energy input:

 

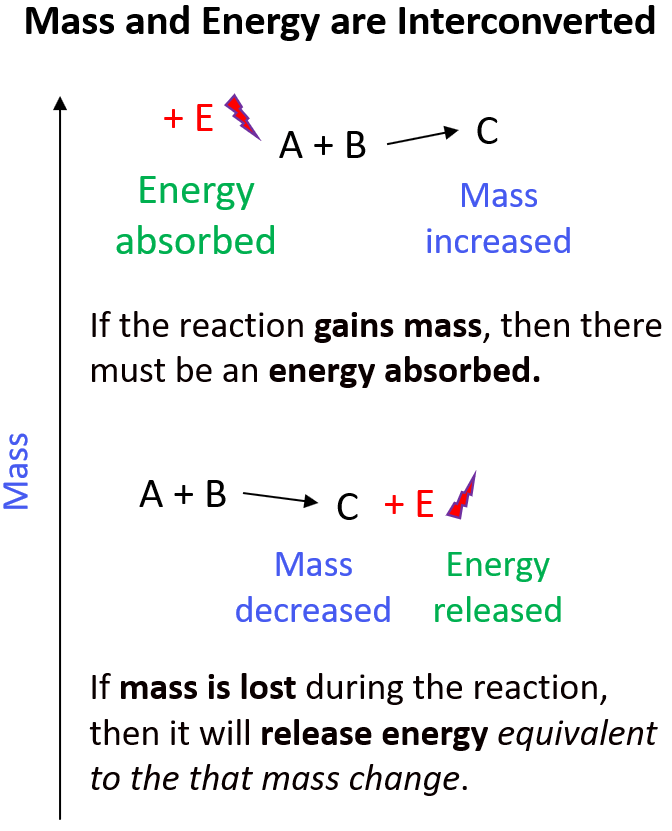
Once again, by comparing the mass loss in the regular combustion and nuclear reactions, we can understand why the latter is associated with a lot more energy.

 

Mass Defect and Nuclear Binding Energy

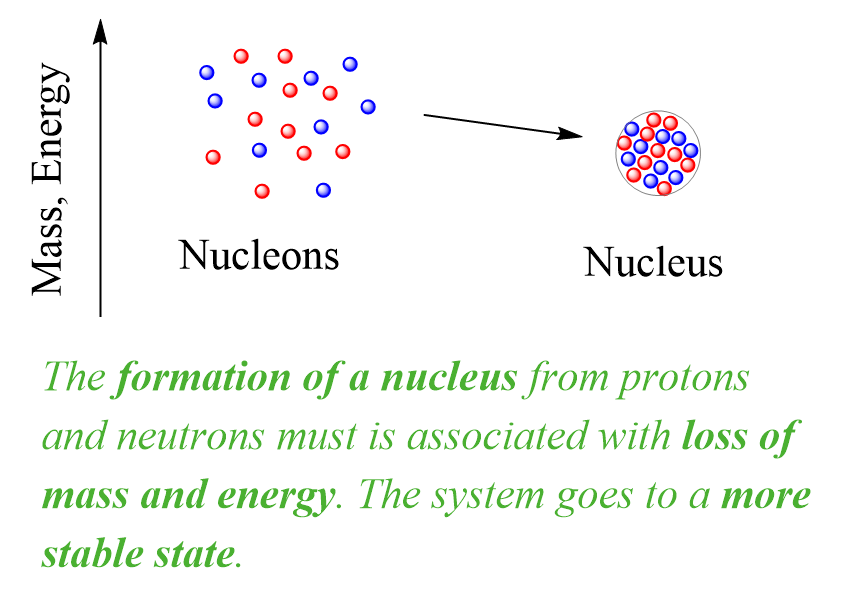
The mass change in nuclear reactions can be better understood by looking at the formation of nuclei from their component particles. It turns out that the masses of nuclei are always less than the sum of the masses of the nucleons (protons and neutrons) they are composed of:

 

 

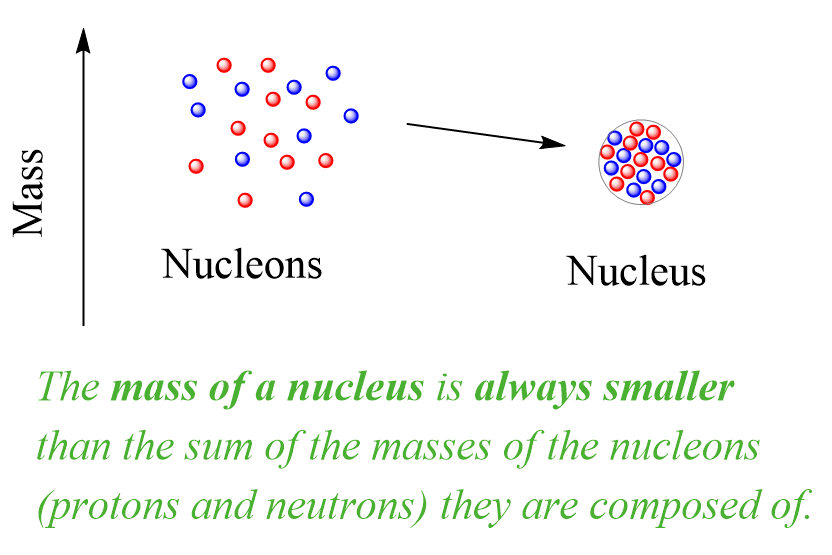
This is the mass defect – the difference between the mass of a nucleus and the sum of the masses of the protons and neutrons it is made of.

 

 

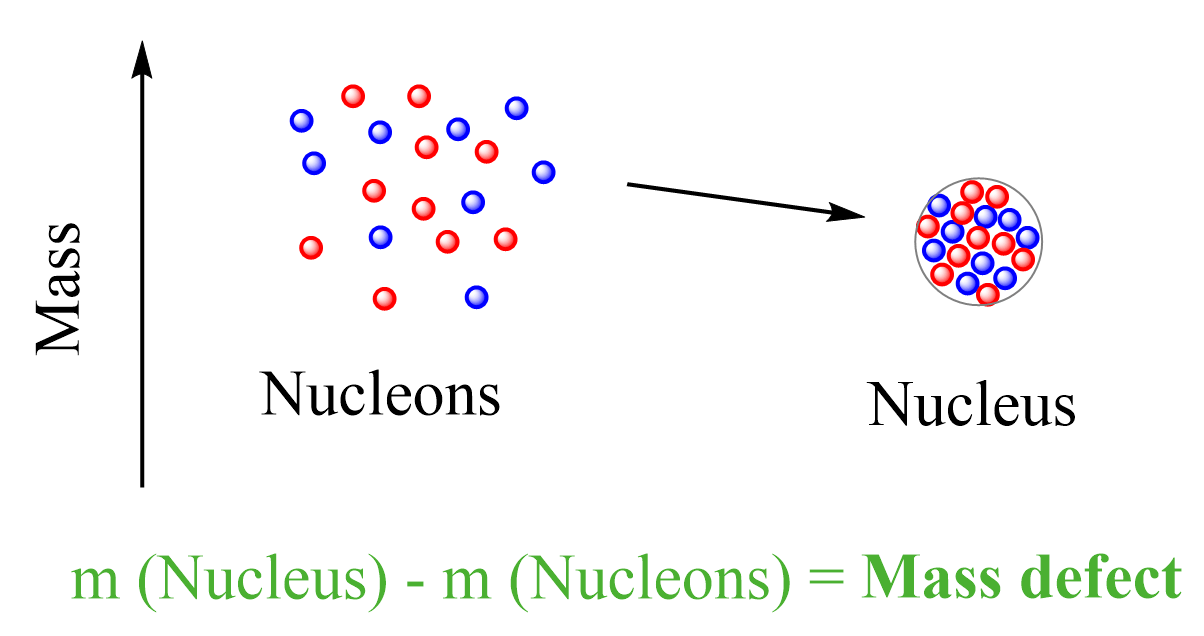
The implication of this mass loss is that the formation of a nucleus from protons and neutrons must be associated with loss of energy. This is like forming a molecule from atoms, once the atoms come to an optimal distance, a chemical bond is formed, and energy is released. Overall, the system goes to a more stable state. Remember, stable means lower energy and the more energy is released during the formation of a molecule or a nucleus, the more stable it is:

 

 

Now, in nuclear chemistry, the term describing the energy change when a nucleus is formed or broken is called nuclear binding energy (BE or E_bind).  Nuclear binding energy is the energy that is needed to break the nucleus into its component nucleons.

 

 

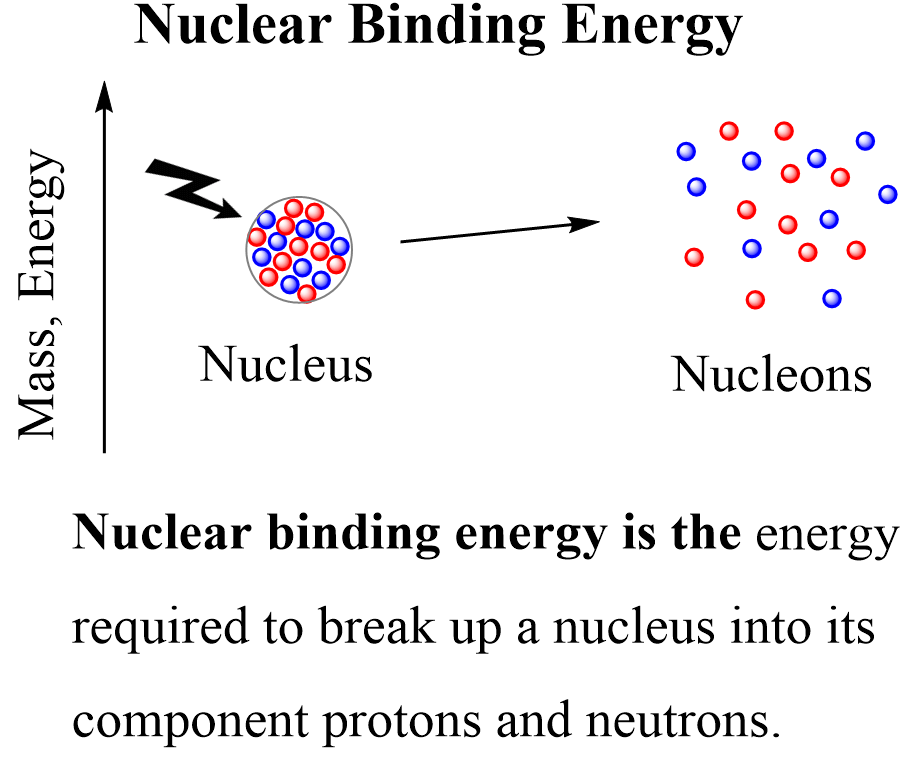
In some textbooks, the nuclear binding energy is associated with the formation of the nucleus and is formulated as the energy released when protons and neutrons come together to form a nucleus. These two are reverse processes and conceptually there is no difference in how we formulate the nuclear binding energy. The analogy to this would be the bond dissociation energy vs the enthalpy of formation.

 

Calculating The Nuclear Binding Energy

Let’s calculate the nuclear binding energy of the ¹²C isotope. For this, we are going to need the masses of the ¹²C atom (12.0 amu), the proton (1.00727647 amu), the neutron (1.008665 amu), and the electron (0.00054858 amu).

First, we will write the equation for breaking carbon into protons and neutrons. The atomic number of carbon is 6, and therefore, it has 6 protons and 12 – 6 = 6 neutrons:

 

¹²C → 6 p + 6 n

 

The mass defect is going to be the difference between the masses of 6 protons + 6 neutrons and the mass of the nucleus of ¹²C. Notice that we are talking about the mass of the nucleus for ¹²C rather than its atomic mass because the nuclear binding energy is referred to the nucleus and its component.

So, how do we find the mass of the nucleus if it’s not given in the problem? Most tables give the atomic masses, and to find the mass of the nucleus, we need to subtract the mass of the electrons in the atom:

m (nucleus) = m (atom) – m (electrons)

The number of electrons in an atom is equal to the number of protons, and therefore, the mass of ¹²C nucleus will be:

m (¹²C nucleus) = m (¹²C atom) – m (6 electrons)

m (¹²C nucleus) = 12.0 amu – 6 x 0.00054858 amu = 11.99671 amu

 

Now, the actual mass defect:

Δm = Σ m (products) – Σ m (reactants)

Δm = 6 x m (p) + 6 x m (n) – m (¹²C nucleus)

Δm = 6 x 1.00727647 amu + 6 x 1.008665 amu – 11.99671 amu

Δm = 12.095649 – 11.99671 = 0.09893882 amu

 

And now, we can calculate the nuclear bind energy using the Einstein’s equation:

 

ΔE = (Δm)c²

 

 Before adding the numbers, remember to convert the amu or grams to kilograms to match the SI units of mass and Joule (kg⋅m²⋅s⁻²). Recall that 1 amu = 1.66054 x 10^-27 kg, therefore:

                                      

\[\Delta m\; = \,0.09893882{\rm{ }}\cancel{{{\rm{amu}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.66054}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 27}}}}\,{\rm{kg}}}}{{{\rm{1}}\,\cancel{{{\rm{amu}}}}}}\; = \,1.6429\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 28}}}}\,{\rm{kg}}\]

 

ΔE = (Δm)c²

ΔE = 1.6429 x 10^-28 kg x (3.00 x 10⁸ m/s)²

ΔE = 1.4786 x 10^-11 kg⋅m²⋅s⁻² = 1.4786 x 10^-11 J

 

Notice that the sign for the mass change and hence the energy change is positive indicating this is how much energy is absorbed for breaking one ¹²C isotope into its component protons and neutrons. If the isotope was formed from these nuclei, then this is how much energy would be released:

 

¹²C → 6 p + 6 n  ΔE = +1.4786 x 10^-11 J

6 p + 6 n → ¹²C  ΔE = –1.4786 x 10^-11 J

 

Do We Have to Use the Mass of Electrons in Nuclear Binding Energy?

As mentioned earlier, the term binding energy refers to the nucleus, and therefore, the mass defect is the difference between the mass of the nucleus and the total mass of the protons and neutrons. Most tables give the atomic masses, and to find the mass of the nucleus, we need to subtract the mass of the electrons in the atom:

 

m (nucleus) = m (atom) – m (electrons)

 

Now, since the total number of electrons does not change, we do not need to subtract the total mass of electrons from the mass of each atom in order to obtain the nuclidic masses (the mass of the nucleus). Instead, we can simply use the atomic masses of the element, and instead of the mass of the proton, we use the mass of the hydrogen atom. Remember, the proton is a hydrogen atom without an electron.

 

So, for our reaction, we can write it as:

 

¹²C → 6 ¹H + 6 n

 

And, in this case, we can use the atomic mass of ¹²C and ¹H to calculate the mass defect without worrying about the mass of electrons:

 

Δm = Σ m (products) – Σ m (reactants)

Δm = 6 x m (¹H) + 6 x m (n) – m (¹²C atom)

Δm = 6 x 1.007825 amu + 6 x 1.008665 amu – 12.00 amu

Δm = 12.09894 – 12.00 = 0.09894 amu

 

As you can see, the mass defect is the same as we had when using the mass of protons, ¹²C nucleus, and 6 electrons, and therefore the energy is also going to be the same.

 

So, the masses of electrons cancel out and therefore, the overall change in mass will be the same in either case. That is the mass defect will be the same whether we use the atomic masses by themselves or the nuclidic masses by subtracting the mass of electrons. Using the atomic masses simply makes the calculations easier because most tables provide the atomic mass rather than the mass of the nucleus. 

This, however, gets trickier in processes such as beta decay and positron emission because the number of electrons in the atoms changes. 

 

The Electron Volt as the Unit of Binding Energy

Using joules to express the binding energy is usually convenient for a mole scale of nuclei, but for a single nucleus, it is too large of a unit to express the binding energy. The more common unit used by nuclear scientists is the electron volt (eV), the energy an electron acquires when it moves through a potential difference of 1 volt:

 

1 eV = 1.602×10⁻¹⁹ J

 

The eV by itself would give too large of numbers, and therefore, binding energies are commonly expressed in mega–electron volts (MeV), so millions of electron volts:

 

1 MeV = 10⁶ eV = 1.602 × 10⁻¹³ J

 

It was determined that the mass change of every atomic mass unit corresponds to a specific energy value, and a very useful factor became popular for quick calculations of energy change from the mass difference:

 

1 amu = 931.5 × 10⁶ eV = 931.5 MeV

 

So, in the previous example, once we knew the mass defect to be 0.09894 amu, we could have directly calculated the binding energy using this conversion factor:

 

\[\Delta E\; = \,\,0.09894{\rm{ }}\cancel{{{\rm{amu}}}}\,{\rm{ \times }}\,\frac{{{\rm{931}}{\rm{.5}}\,{\rm{MeV}}}}{{{\rm{1}}\,\cancel{{{\rm{amu}}}}}}\;{\rm{ = }}\,{\rm{92}}{\rm{.16}}\,{\rm{MeV}}\]

 

Nuclear Binding Energy Per Nucleon

Nuclear binding energy is the energy needed to break the nucleus into its component nucleons. So, logically, the more nucleons (protons and neutrons) there are, the more energy will be needed to separate them. This, however, is not an indicator of how much more or less stable a given nucleus is compared to another one. We can think about it this way: it may be more difficult to break 10 plastic sticks together than one metallic stick, but that would not mean than the plastic stick is stronger. We need to compare the same number of units, and for this, nuclear binding energy per nucleon is used. So, if the nucleus consists of 10 neutrons and 8 protons, for example, then we will divide the binding energy by 18 as there are 18 nucleons in it. In the case of ¹²C isotope, we would need to divide the 1.4786 x 10^-11 J binding energy by 12:

                                                  

\[BE\,{{\rm{(}}^{{\rm{12}}}}{\rm{C)}}\,{\rm{ = }}\,\frac{{{\rm{1}}{\rm{.4786}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 11\;}}}}{\rm{J}}}}{{{\rm{12}}\,{\rm{nucleons}}}}\;{\rm{ = }}\,{\rm{1}}{\rm{.232}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 12\;}}}}{\rm{J/nucleon}}\]

 

Let’s do another example, calculate the nuclear binding energy per nucleon for ⁵⁶Fe given its atomic mass is 55.934939 am, mass of ¹H atom = 1.007825 amu; mass of neutron = 1.008665 amu.

 

First, write the nuclear equation for a better visualization of the process. Iron has 26 protons and 30 neutrons:

 

⁵⁶Fe → 26 ¹H + 30 n

 

The mass difference would be:

 

Δm = Σ m (products) – Σ m (reactants)

Δm = 26 x m (¹H) + 30 x m (n) – m (⁵⁶Fe atom)

Δm = 26 x 1.007825 + 30 x 1.008665– 55.934939 = 0.52846 amu

 

And now, we can calculate the binding energy per nucleon in MeV using the conversion factor 1.00 amu = 931.5 MeV:

 

\[\Delta E\; = \,\,\frac{{{\rm{0}}{\rm{.52846 amu}}\,{\rm{ \times }}\,{\rm{931}}{\rm{.5}}\,{\rm{MeV}}}}{{{\rm{56}}\,{\rm{nucleons}}}}\;{\rm{ = }}\,{\rm{8}}{\rm{.790}}\,{\rm{MeV/nucleon}}\]

 

To calculate the binding energy in Joules, we convert the amu to kg first:

 

\[\Delta m\; = \,0.52846{\rm{ }}\cancel{{{\rm{amu}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.66054}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 27}}}}\,{\rm{kg}}}}{{{\rm{1}}\,\cancel{{{\rm{amu}}}}}}\; = \,8.7753\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 28}}}}\,{\rm{kg}}\]

 

ΔE = 8.7753 x 10^-28 kg x (3.00 x 10⁸ m/s)²

ΔE = 7.898 x 10^-11 kg⋅m²⋅s⁻² = 7.898 x 10^-11 J

 

This is the nuclear binding energy of one ⁵⁶F nucleus, and to find it per nucleon, we need to divide the value by 56 (26 protons and 30 neutrons):

 

\[BE\,{{\rm{(}}^{{\rm{56}}}}{\rm{Fe)}}\,{\rm{ = }}\,\frac{{{\rm{7}}{\rm{.898}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 11\;}}}}{\rm{J}}}}{{{\rm{56}}\,{\rm{nucleons}}}}\;{\rm{ = }}\,{\rm{1}}{\rm{.41}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 12\;}}}}{\rm{J/nucleon}}\]

 

Comparing the binding energy per nucleon, we can see that ⁵⁶Fe is more stable than ¹²C, and in general, the A ≈ 60 amu happens to have the most stable nuclei which explains why, together with nickel, iron is so abundant on planet Earth and most meteorites.

 

Nuclear Binding Energy and Stability of Nuclei

Nuclear binding energy per nucleon is used as a measure of nuclear stability. The greater the binding energy per nucleon, the more stable the nuclide is. The approximate sketch of the plot showing the binding energy (in MeV per nucleon) vs the atomic mass shows that the most stable elements are in the region of ~60 amu. The binding energy increases up to this region and then goes down as we move toward heavier elements:

 

 

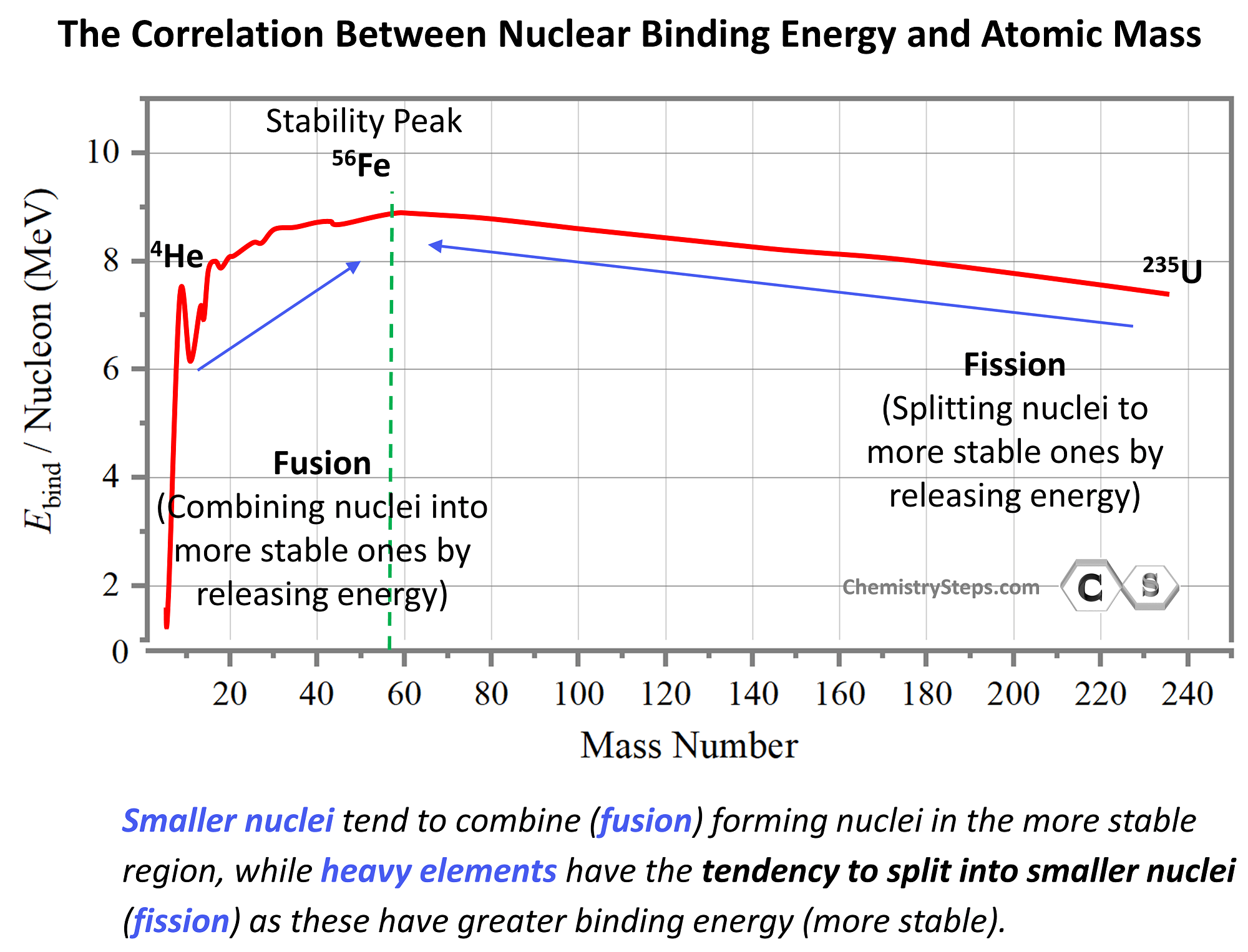
We can predict important trends for nuclear reactions based on the binding energies. For example,  we can predict that smaller nuclei will tend to combine (fusion) forming nuclei in the more stable region, while heavy elements, being unstable, will have the tendency to split into smaller nuclei (fission) as these have greater binding energy (more stable).

This may seem counterintuitive by looking at the energy graph since fusion and fission appear to be going uphill. However, this is simply because the energy scale shows the energy needed to break nuclei rather than forming them. By mirroring the graph, we can show the energy released when a nucleus is formed, and in this case, the most stable nuclei will appear in the downhill region:

 

 

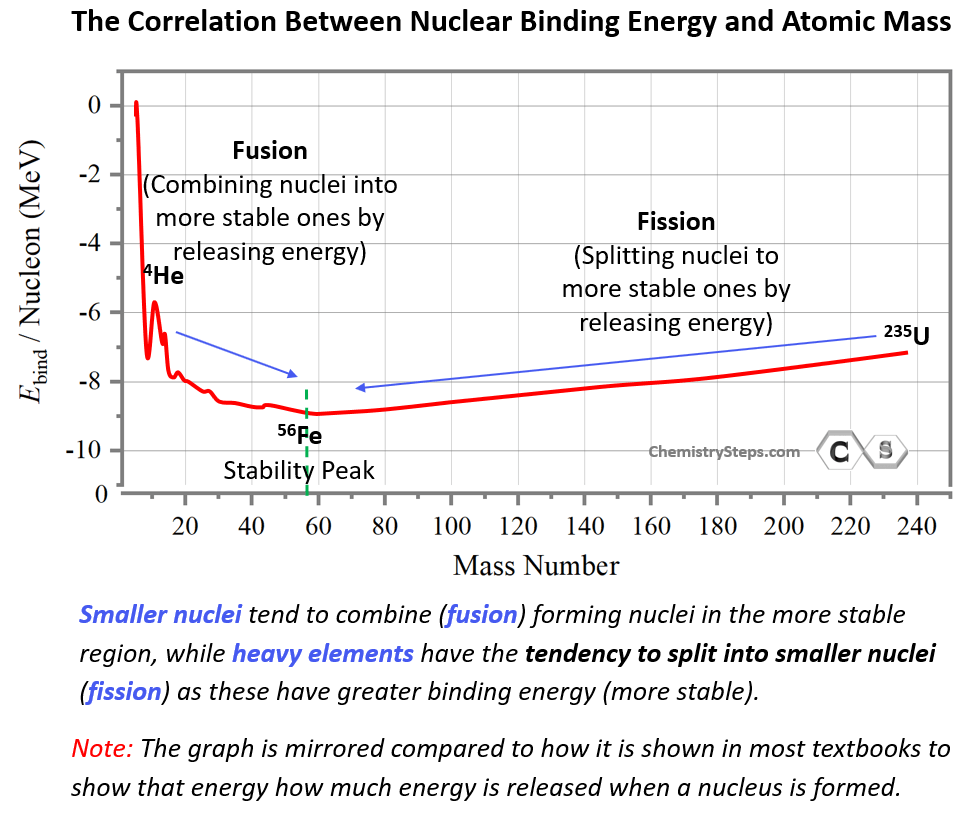
So, the more energy is released when the nucleus is formed, the more stable it is, and this shows why smaller nuclei have the tendency to undergo fusion (form new elements) in the A = 60 amu region, while heavy nuclei will tend to undergo fission (break into smaller elements).   

An example of a fusion is the reaction in the core of the Sun where hydrogen is being converted into helium. Although the process consists of several steps, overall, it takes four hydrogen atoms to fuse into each helium atom. During the process, some of the mass is converted into energy.

 

4 ¹₁H → ⁴₂He + 2 ⁰₁β + Energy

 

Fission, on the other hand, is energetically profitable from heavier elements. For example, the uranium-235 isotope undergoes nuclear fission when bombarded with neutrons according to the following equation:

 

²³⁵₉₂U + ¹₀n→ ¹⁴⁰₅₆Ba + ⁹³₃₆Kr + 3 ¹₀n + Energy

 

Now, both nuclear fusion and fission reactions often require energy input, and sometimes huge amounts of it, so when we say that smaller nuclei have the tendency to undergo fusion, we are talking about the overall energy change of the process, but in order for it to occur a huge activation energy barrier must be overcome. Recall from kinetics and thermodynamics that activation energy shows how fast the reaction can occur while thermodynamics shows whether the overall process is energetically favorable or not.

 

 

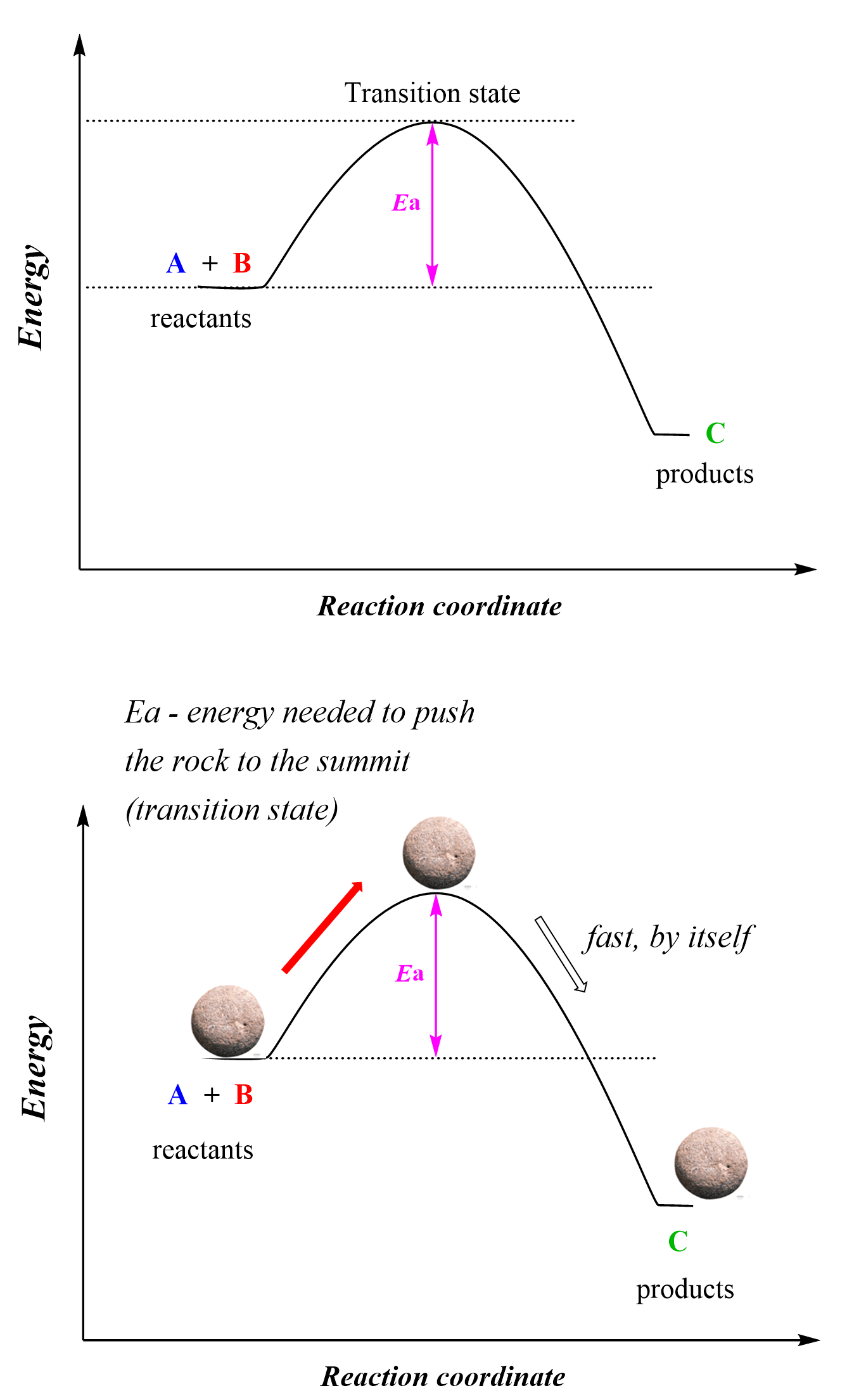
So, for the tendencies of fusion and fission, we are saying that the fusion of smaller elements into new ones in the A ≈ 60 region is energetically favorable – exothermic, while fission is exothermic for heavier elements. We will talk more about nuclear fusion and fission in the next article.

 

Here is a 73-question, Multiple-Choice Quiz on Nuclear Chemistry:

 

Check Also

• Alpha Particles, Beta Particles, and Gamma Rays
• Balancing Nuclear Reactions
• Carbon Dating Practice Problems
• Half-Life and Radioactivity Practice Problems
• The energy of Nuclear Reactions
• Nuclear Fission and Fusion