Before discussing the standard cell potential, let’s remember that it applies to electrochemical cells. An electrochemical cell is a system where a redox reaction occurs between two cells that are connected by a wire.
In an electrochemical cell, one component undergoes oxidation by giving the electrons to the other which is reduced. The electrode where oxidation occurs is the anode and the electrode where reduction occurs is the cathode, and this is true for all electrochemical cells.
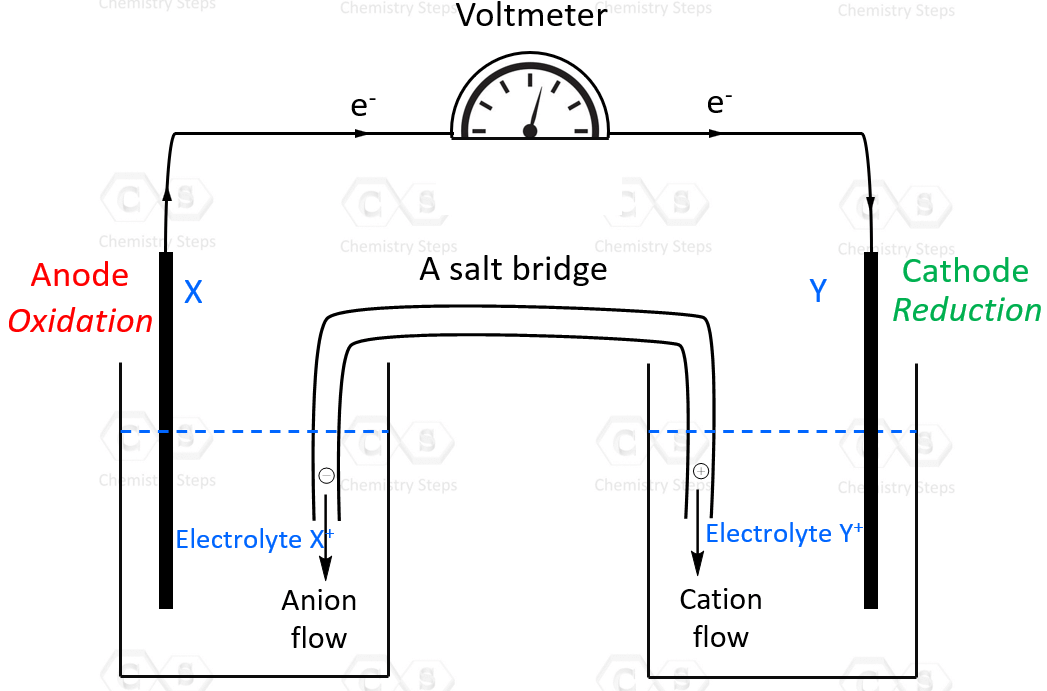
The standard cell potential (E°cell) is measured at 298 K and all components in their standard states: 1 atm for gases, 1 M for solutions, and the pure solid for electrodes.
Overall, the cell potential is the difference in voltage between the cathode and the anode.
Eocell = Eocathode – Eoanode
Calculating the Standard Cell Potential
For example, let’s calculate the standard cell potential of the following redox reaction:
Zn(s) + Sn2+(aq) → Zn2+(aq) + Sn(s)
Most often you will need to identify the half-reactions to be able to find the values of standard reduction potentials for most half-reactions in your textbook. Remember, the potential of each cell is measured relative to the potential of the standard hydrogen cell which is set to 0 V.
In this example, we already know which metal is reduced and which one is oxidized, and we will see examples where we will need to determine this.
We can see that Zn turns into a cation and Sn2+ is reduced to Sn, so all we need to do is show these processes separately with their reduction potentials from the textbook.
So, the first thing here is to identify the half-reactions and look up the value for each cell potential in the table of standard reduction potentials.
Before proceeding forward, I want to mention that this method might be different that what your textbook does. This method seemed to be less confusing to my students, and that is how will do in these practice problems, but we will get to that and discuss the other approach as well.
Based on the overall reaction, these would be the two half-reactions:
Zn(s) → Zn2+(aq) + 2e–
Sn2+(aq) + 2e– → Sn(s)
Next is finding the standard reduction potentials and you need to make sure to switch the sign of the cell potential if the reaction is reversed. For example, the standard reduction potential of Sn2+ is -0.14 V and that for the reaction: Sn2+(aq) + 2e– → Sn(s). Therefore, we do not need to change the value from negative to positive, and the half reaction can be written as:
Sn2+(aq) + 2e– → Sn(s) Eo = -0.14 V
For Zn, however, the standard reduction potential is -0.76 V for the reaction Zn2+(aq) + 2e– → Zn(s), and because Zn is oxidized in our example, we need to switch the sign from negative to positive:
Zn(s) → Zn2+(aq) + 2e– Eo = +0.76 V
Once we have the half-reactions with the correct standard reduction potentials written, we can calculate the Eocell by simply adding the numbers together:
Eocell = +0.76 V + (-0.13 V) = 0.63 V
Notice that cell potential is positive, therefore, the reaction is spontaneous which is how a galvanic cell (voltaic cell) must be.
Let’s now discuss the other method commonly used in textbooks.
What we did above is looked up the values of Eo and changed the sign of Eo for the reaction that is reversed. In this case, it is the oxidation of Zn. The Eo (Zn2+ → Zn(s)) is -0.76 V and because we have the reverse reaction, we changed the sign and simply added the Eo values to find the cell potential.
Alternatively, and this is what you will see in most textbooks, the signs of Eo are not changed for reversed reactions, and instead, the traditional formula for the cell potential is used which is the difference between the potential of the cathode and the anode:
Eocell = Eocathode – Eoanode
In this example, Zn(s) → Zn2+(aq) + 2e– is the oxidation, and therefore, it occurs on the anode. The Eoanode = -0.76 V as per the table of standard reduction potentials. Eocathode, then is equal to -0.13 V, and the cell potential would be:
Eocell = Eocathode – Eoanode = -0.13 V – (-0.76 V) = 0.63 V
Cell Potential When the Overall Reaction is Not Given
Let’s now consider an example where the overall redox reaction is not given. In other words, we do not know which species undergoes oxidation and which one is reduced.
For example, calculate the cell potential of the galvanic cell prepared with Ni/Ni2+ and Mn/Mn2+ components. As a bonus, sketch a voltaic cell, label the anode and cathode, and indicate the half-reaction that occurs at each electrode. Show the direction of electron flow and the species present in each solution.
The first thing you need to pay attention here is the fact that it is a galvanic cell and therefore, the reaction we come up with should be spontaneous, and therefore, the cell potential must be a positive value.
So, let’s look up the standard reduction potentials for Ni2+ and Mn2+:
Ni2+(aq) + 2e– → Ni(s)Eo = -0.23 V
Mn2+(aq) + 2e– → Mn(s) Eo = -1.18 V
Both reactions have negative standard cell potentials, and therefore, we need to reverse one of them because as it is, they both represent a reduction, and we know that one of them must be an oxidation. One reaction must give the electrons and the other accept them.
If we reverse the first reaction, the cell potential will have a negative value and therefore, the reaction won’t be spontaneous because the cell potential will be negative:
Ni(s)→Ni2+(aq) + 2e–Eo = +0.23 V
Mn2+(aq) + 2e– → Mn(s) Eo = -1.18 V
Eocell = +0.23 V + (-1.18 V) = -0.95 V
Therefore, it is the second reaction that needs to be reversed:
Ni2+(aq) + 2e– → Ni(s)Eo = -0.23 V
Mn(s) → Mn2+(aq) + 2e– Eo = +1.18 V
Eocell = -0.23 V + (+1.18 V) = +0.95 V
So, Ni2+ will undergo a reduction in this reaction (cathode), and Mn will be oxidized (anode). We can also see this from the standard reduction potentials: Ni2+ stands above in the list of standard reduction potentials, and therefore, it has a greater tendency to accept electrons and thus undergo a reduction than Mn2+.
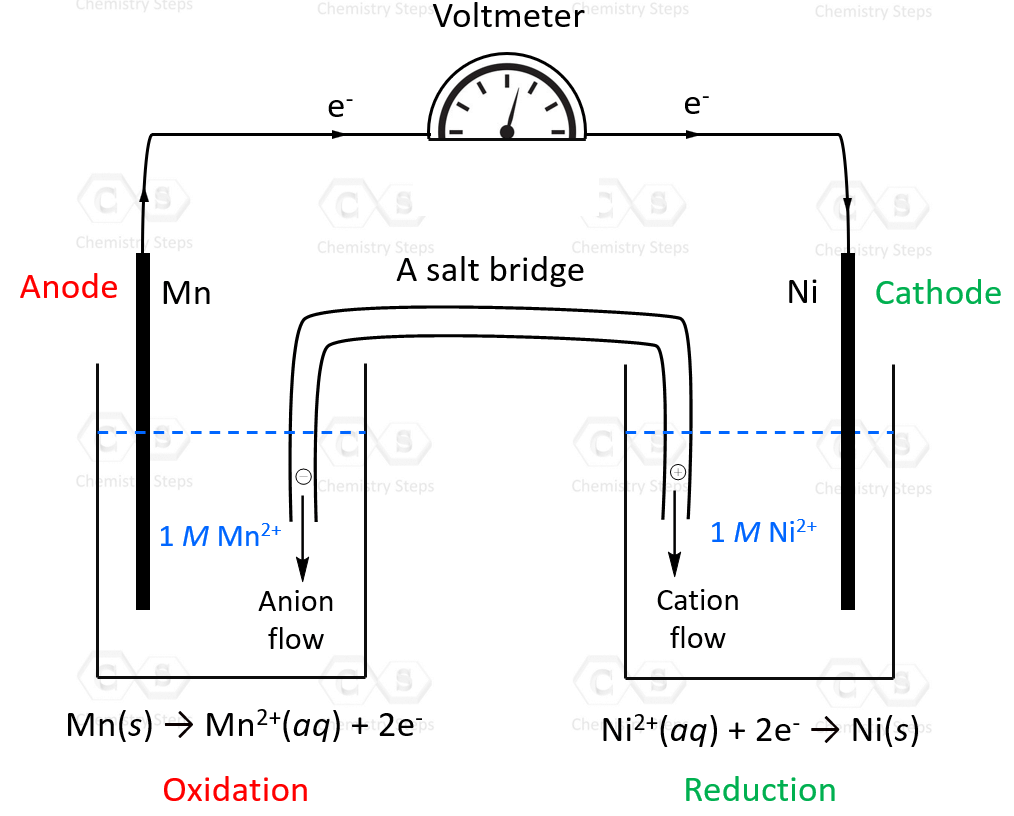
The overall reaction can be determined by adding the correct half-reactions:
Ni2+(aq) + 2e– → Ni(s)Eo = -0.23 V
+
Mn(s) → Mn2+(aq) + 2e– Eo = +1.18 V
________________________________________
Ni2+(aq) + 2e– + Mn(s) → Ni(s) + Mn2+(aq) + 2e–
Ni2+(aq) + Mn(s) → Ni(s) + Mn2+(aq) Eocell = 0.95 V
The Coefficients and Standard Cell Potential
We have seen that reversing a redox reaction must be done by switching the sign of the cell potential. Recall that this is similar to the enthalpy or Gibbs free energy of the reaction. However, unlike those, when we multiply the half reactions by any coefficient in order to balance the number of electrons and all the species, we do NOT apply that coefficient to the cell potential. This means that the value of E° is does not depend on the size of the electrodes or the amount of solutions present. So, switching from a tiny electrode to huge one won’t suddenly make the current life-threatening. Keep in mind though that it does depend on the concentration of the species, and we will discuss this in the next article.
For example, calculate the standard cell potential of for the reaction between these two species and determine if it is spontaneous:
2Al(s) + 3Cu2+(aq) → 2Al3+(aq) + 3Cu(s)
Let’s follow the steps we discussed above to do this.
1) Separate the half-reactions, and switch the sign of Eofor the reaction that is reversed compared to how it is shown in the list of standard reduction potentials:
Al(s) → Al3+(aq) + 3e– Eo = +1.66 V
Cu2+(aq) + 2e– → Cu(s) Eo = +0.34 V
To balance the number of electrons in both equations, we multiply the first by 2 and the second by 3, and the number of electrons will be six:
2Al(s) → 2Al3+(aq) + 6e– Eo = +1.66 V
3Cu2+(aq) + 6e– → 3Cu(s) Eo = +0.34 V
Adding coefficients to balance the number of electrons is always a good practice. However, we did not do it here because remember, coefficients do not affect the potential of a reaction.
2) Calculate the Eocell by adding the potentials of the two reactions:
Eocell = 1.66 V + 0.34 V = 2.00 V
The cell potential is positive, and therefore, the reaction is spontaneous.
Check Also
- Balancing Redox Reactions
- Galvanic Cells
- The Correlation Between Eocell, ΔG°, and K
- Nernst Equation
- Nernst Equation Practice Problems
- Concentration Cells
- Electrolytic Cells
- Electrolysis
- Electrolysis of Water
- Calculating the Mass of Metal in Electroplating
- Cell Potential Practice Problems
- Eo, ΔGo, K – Practice Problems
- Electrochemistry Practice Problems
Practice
Calculate the cell potential for each redox reaction and determine if it is spontanesous or not:
a) Zn(s) + Pb2+(aq) → Zn2+(aq) + Pb(s)
b) 2Cl–(aq) + Pb2+ (aq) → Cl2(l) + Pb(s)
c) Cd(s) + Pb2+(aq) → Cd2+(aq) + Pb(s)
d) Fe(s) + 3Ag+(aq) → Fe3+(aq) + 3Ag(s)
e) Ca2+(aq) + Fe(s) → Ca(s) + Fe2+(aq)
f) Ni(s) + Mg2+(aq) → Ni2+(aq) + Mg(s)
g) Sn2+(aq) + Mg(s) → Sn(s) + Mg2+(aq)
h) Br2(l) + 2I–(aq) → 2Br–(aq) + I2(s)
i) 2Al(s) + 3Cu2+(aq) → 2Al3+(aq) + 3Cu(s)
j) O2(g) + 4H+(aq) + Cu(s) → Cu2+(aq) + 2H2O(l)
k) MnO2(s) + 4H+(aq) + Cd(s) → Mn2+(aq) + 2H2O(l ) + Cd2+(aq)

