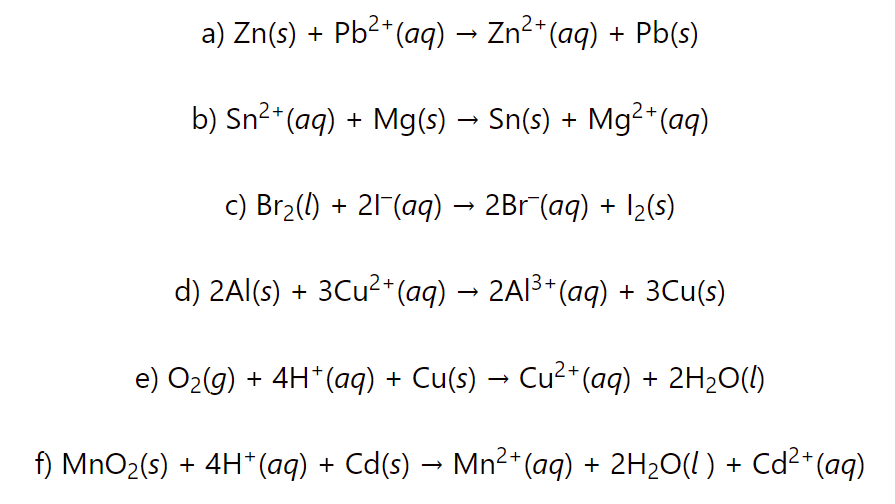Calculate the cell potential, Gibbs free energy change ΔG°, and equilibrium constant, K for each redox reaction:
a) Zn(s) + Pb2+(aq) → Zn2+(aq) + Pb(s)
b) Sn2+(aq) + Mg(s) → Sn(s) + Mg2+(aq)
c) Br2(l) + 2I–(aq) → 2Br–(aq) + I2(s)
d) 2Al(s) + 3Cu2+(aq) → 2Al3+(aq) + 3Cu(s)
e) O2(g) + 4H+(aq) + Cu(s) → Cu2+(aq) + 2H2O(l)
f) MnO2(s) + 4H+(aq) + Cd(s) → Mn2+(aq) + 2H2O(l ) + Cd2+(aq)
ΔG° is correlated to Eocell with the following formula:
ΔG° = –nFEocell
Where n is the moles of electrons and F is the Faraday’s constant which is equal to 96,485 C. Therefore, the plan is to first calculate the cell potential and then use it to determine the ΔG°.
There are two equations we can use to calculate the equilibrium constant. One is linked through the Eocell, and the other, through the ΔG° which is also calculated through the Eocell. Yes, we can calculate the ΔG° using the standard free energies of formations, however, this is not related to electrochemistry and we won’t focus on that here.
\[{E^o}_{{\rm{cell}}}\, = \,\frac{{0.0257\;{\rm{V}}}}{n}\,\ln \,K\]
\[K\; = \;{e^{\frac{{nE}}{{0.0257}}}}\]
For reaction (a), Eocell = 0.63 V, therefore, K would be:
\[K\; = \;{e^{\frac{{2\, \cdot \,0.63}}{{0.0257}}}}\, = \,{e^{49.0}}\, = \;1.91\, \times \,{10^{21}}\]
The second approach:
The equilibrium constant is correlated with the standard free energy change (ΔG°) by this formula:
ΔG° = –RT ln K
Therefore, the equilibrium constant would be equal to:
\[\ln \,K\; = \;\frac{{ – \Delta G^\circ }}{{RT}}\]
\[K\; = \;{e^{\frac{{ – \Delta G^\circ }}{{RT}}}}\]
For the next problems, we will use the first approach to calculate the K.
This content is available to registered users only.
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Check Also
- Balancing Redox Reactions
- Galvanic Cells
- How to Calculate Standard Cell Potential
- The Correlation Between Eocell, ΔG°, and K
- Nernst Equation
- Nernst Equation Practice Problems
- Concentration Cells
- Electrolytic Cells
- Electrolysis
- Electrolysis of Water
- Calculating the Mass of Metal in Electroplating
- Cell Potential Practice Problems
- Eo, ΔGo, K – Practice Problems
- Electrochemistry Practice Problems
General Chemistry