We mentioned in the previous post that the equilibrium-constant expression can be formulated in terms of partial pressures when the reactants and products in a chemical reaction are gases.
For example, when the equilibrium constant of the reaction between sulfur dioxide and oxygen, can be expressed based on the molar concentrations (Kc) or the partial pressures (Kp):
2SO2(g) + O2(g) ⇆ 2SO3(g)
\[{K_c} = \frac{{{{\left[ {{\rm{S}}{{\rm{O}}_{\rm{3}}}} \right]}^2}}}{{{{\left[ {{\rm{S}}{{\rm{O}}_{\rm{2}}}} \right]}^2}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}\]
\[{K_p} = \frac{{{P^2}_{{\rm{S}}{{\rm{O}}_{\rm{3}}}}}}{{{P^{\rm{2}}}{{_{{\rm{SO}}}}_{_2}}{P_{{{\rm{O}}_{\rm{2}}}}}}}\]
Where PSO3, PSO2, and PO2 are the partial pressure of the reaction components.
The subscript p on K is used to point out that the equilibrium constant Kp is defined using partial pressures.
For a general reaction of gases, the equilibrium constant Kp can be represented as:
aA + bB ⇆ cC + dD
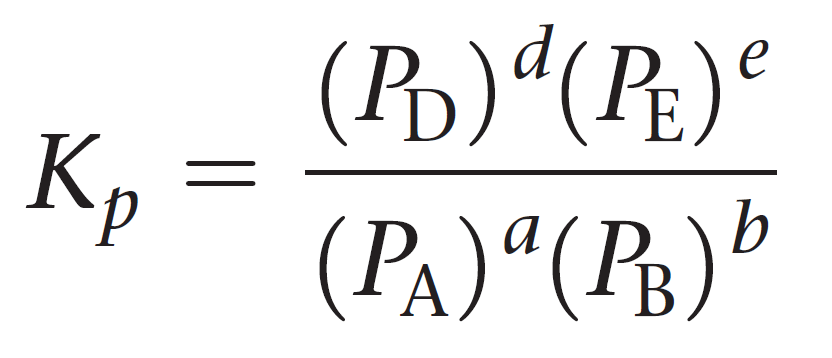
Let’s see an example of calculating Kp.
Example:
The following equilibrium pressures were observed at a certain temperature for the Haber process:
3H2(g) + N2(g) ⇆ 2NH3(g)
P(NH3) = 5.2 x 109 atm
P(N2) = 6.1 x 102 atm
P(H2) = 4.7 x 103 atm
Calculate the value for the equilibrium constant Kp at this temperature.
Solution:
\[{K_p} = \frac{{{P^2}_{{\rm{N}}{{\rm{H}}_{\rm{3}}}}}}{{{P^3}_{{{\rm{H}}_{\rm{2}}}}{P_{{{\rm{N}}_{\rm{2}}}}}}}\]
\[{K_p} = \frac{{{{(5.2 \times {{10}^9})}^2}}}{{{{(4.7 \times {{10}^3})}^3}(6.1 \times {{10}^2})}} = 4.3 \times {10^5}\]
The Relationship Between Kp and Kc
Although the values of Kp and Kc are generally different, it is possible to calculate one from the other using the ideal gas law equation. The idea is to rearrange the ideal gas law equation to get an expression for the partial pressure of each gas and use in the equation of Kp.
PV = nRT, so for P, we can write:
\[P\; = \;\frac{n}{V}RT\]
Remember that n/V is the molarity, so the partial pressure of gas “A” is equal to:
\[{P_A}\; = \;\frac{{{n_A}}}{V}RT\; = \,\left[ {\rm{A}} \right]RT\]
The equivalent expression for the partial pressure of each gas is then entered in the equation of Kp:
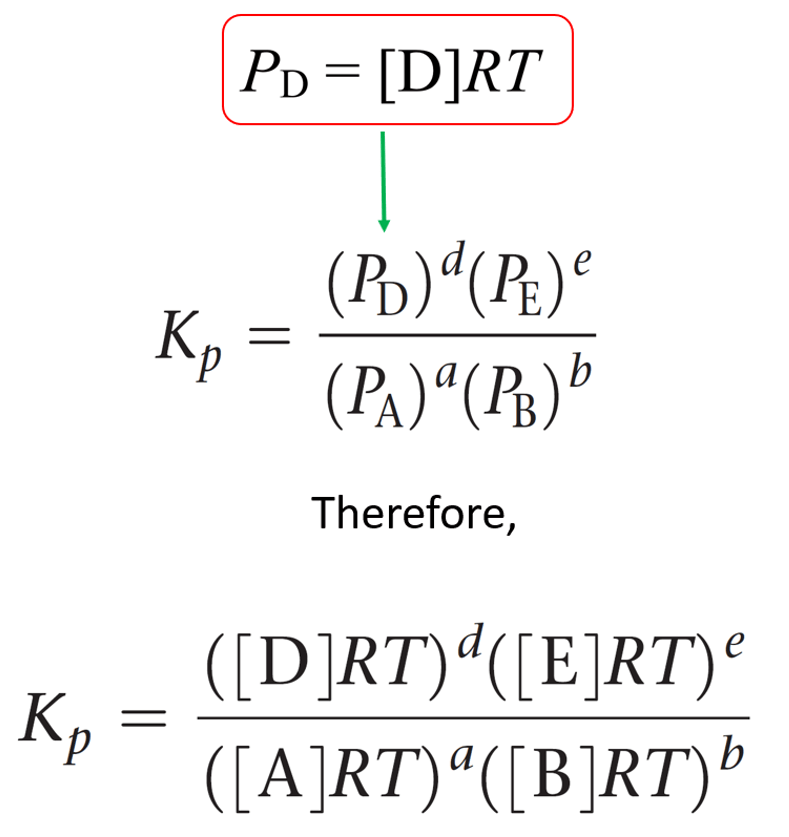
This expression is then simplified by separating the terms of concentration and RT:
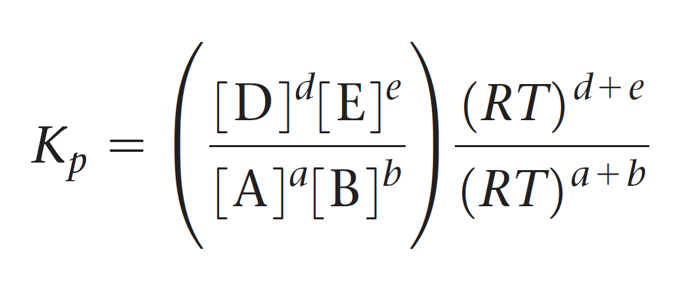
And now the cool part; Notice that the term in brackets on the left side is equal to Kc, so we can further simplify this expression:
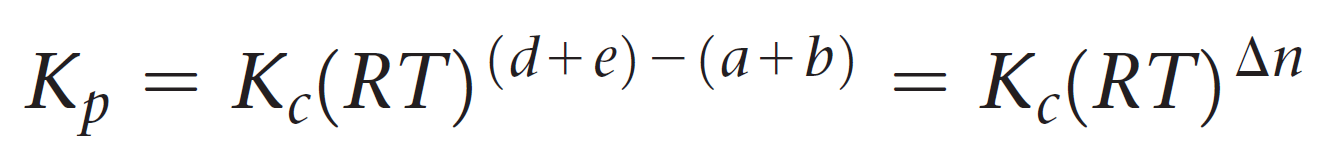
Let’s put this as separate formula correlating Kp and Kc since you are going to use it quite often when solving equilibrium problems:
aA + bB ⇆ cC + dD
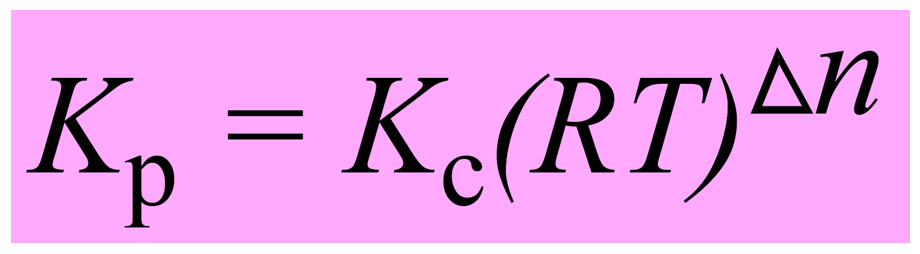
The quantity Δn is the number of moles of gaseous products minus the number of moles of gaseous reactants.
Δn = (c + d) – (a + b)
R is the gas constant, 0.08206 (L · atm)/ (K · mol) , and T is the absolute temperature in Kelvins.
For example, the decomposition of 1 mol of N2O4 produces 2 mol of NO2, soΔn = 2 – 1 = 1, and Kp = Kc(RT):
N2O4(g) ⇆ 2NO2(g)
The equilibrium constant of this reaction is Kc = 4.6 x 10-4 , and therefore, Kp = K(RT) = 4.6 x 10-4(0.08206 L · atm/K · mol × 298 K) = 1.1 x 10-2.
Another example: The Kc for the synthesis reaction of ammonia at a certain temperature is 6.7 x 109. Calculate the Kp of the reaction.
3 H2(g) + N2(g) ⇆ 2 NH3(g)
There are more reactant than product molecules in the equation, so the is going to be a negative number:
Δn = 2- (3+ 1) = -2
Kp = K(RT) = 6.7 x 109 (0.08206 L · atm/K · mol × 298 K)-2 = 1.6 x 1011
When the number of products and reactant molecules is equal, then Kc = Kp because Kp = K(RT)0 = K.
For example, suppose the Kc of the reaction between hydrogen and bromine gases is 5.20 x 1018.
H2(g) + B2(g) ⇆ 2HBr(g) Kc = 5.20 x 1018
Determine the Kp of this reaction.
Solution: Kp = K(RT)0 = K = 5.20 x 1018
Kp Changes with Chemical Equation
The expression of Kp changes with the chemical equation just like we saw it for Kc.
Kp for the reverse reaction
The following reaction has an equilibrium constant of Kp = 4.42 x 10-5 at 298 K:
CH3OH(g) ⇆ CO(g) + 2H2(g)
Calculate the equilibrium constant for this process if the reaction is represented as follows:
CO(g) + 2H2(g) ⇆ CH3OH(g)
Remember, when a reaction is reversed, then Knew = 1/Koriginal.
Therefore,
Knew = 1/Koriginal= 1/4.42 x 10-5= 22,624.43 = 2.26 x 104
Kp When the Coefficients are Changed
Based on the Kp value given above, what is the Kp for the following reaction?
2CH3OH(g) ⇆ 2CO(g) + 4H2(g)
Comparing this equation to the original, we see that it is multiplied by 2. Remember when the coefficients in the equation are multiplied by any factor, we raise the equilibrium constant to the same factor. Therefore,
Knew = (Koriginal)n = (4.42 x 10-5)2= 1.96 x 10-9
Practice
Consider the following reactions:
1) H2(g) + I2(g) ⇆ 2HI(g)
2) H2(g) + I2(s) ⇆ 2HI(g)
In which reaction are the K and Kp equal?
At 300 K, the equilibrium concentrations for the following reaction are [CH3OH] = 0.240 M, [CO] = 0.350 M, and [H2] = 1.65 M for the reaction
CH3OH(g) ⇆ CO(g) + 2H2(g)
Calculate Kp at this temperature.
Given the equilibrium constant, calculate Kp for each of the following reactions at 298 K.
a) N2O4(g) ⇆ 2NO2(g) Kc = 4.6 x 10-4
b) 3H2(g) + N2(g) ⇆ 2NH3(g) Kc = 6.7 x 109
c) H2(g) + B2(g) ⇆ 2HBr(g) Kc = 5.20 x 1018
Calculate Kc for each reaction.
a) CO(g) + Cl2(g) ⇆ COCl2(g) Kp = 5.3 x 106
b) CH4(g) + H2O(g) ⇆ CO(g) + 3H2(g) Kp = 7.7 x 108
c) 2SO2(g) + O2(g) ⇆ 2SO3(g) Kp = 6.26 x 105
Check Also
- Chemical Equilibrium
- Equilibrium Constant
- Kpand Partial Pressure
- Kp and KcRelationship
- K Changes with Chemical Equation
- Equilibrium Constant K from Two Reactions
- Reaction Quotient – Q
- ICE Table – Calculating Equilibrium Concentrations
- ICE Table Practice Problems
- Le Châtelier’s principle
- Le Châtelier’s principle Practice Problems
- Chemical Equilibrium Practice Problems
