Vapor pressure lowering is a colligative property of solutions. So, first, what is vapor pressure?
Recall that when a liquid evaporates in a closed container, an equilibrium is established between the liquid and the gas, and the pressure exerted by the vapor is called the vapor pressure. Now, the more the liquid evaporates, the more gas is formed and therefore, the higher the vapor pressure.
It turns out that when a nonvolatile solute is added to the solvent, the vapor pressure of the solvent in the solution decreases compared to what it was for pure solvent.
For example, if we add NaCl to water, the vapor pressure of the solution is lower than that of water:
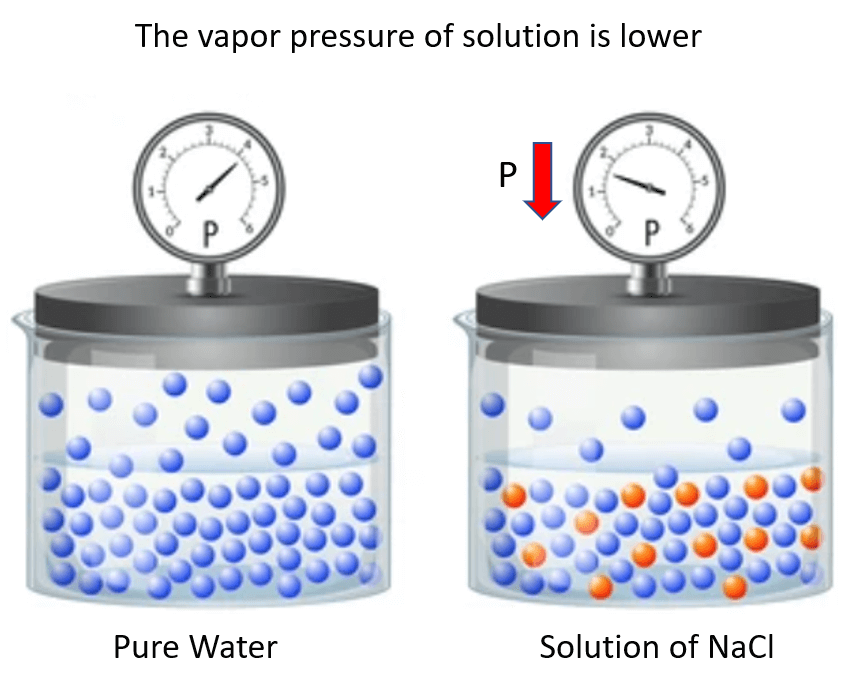
One way to explain this behavior is the interference of the solute particles to the evaporation of the solvent molecules. This can be, for example, some intermolecular interactions between these species. In other words, let’s say the solute particles “get on the way” of evaporating solvent molecules.
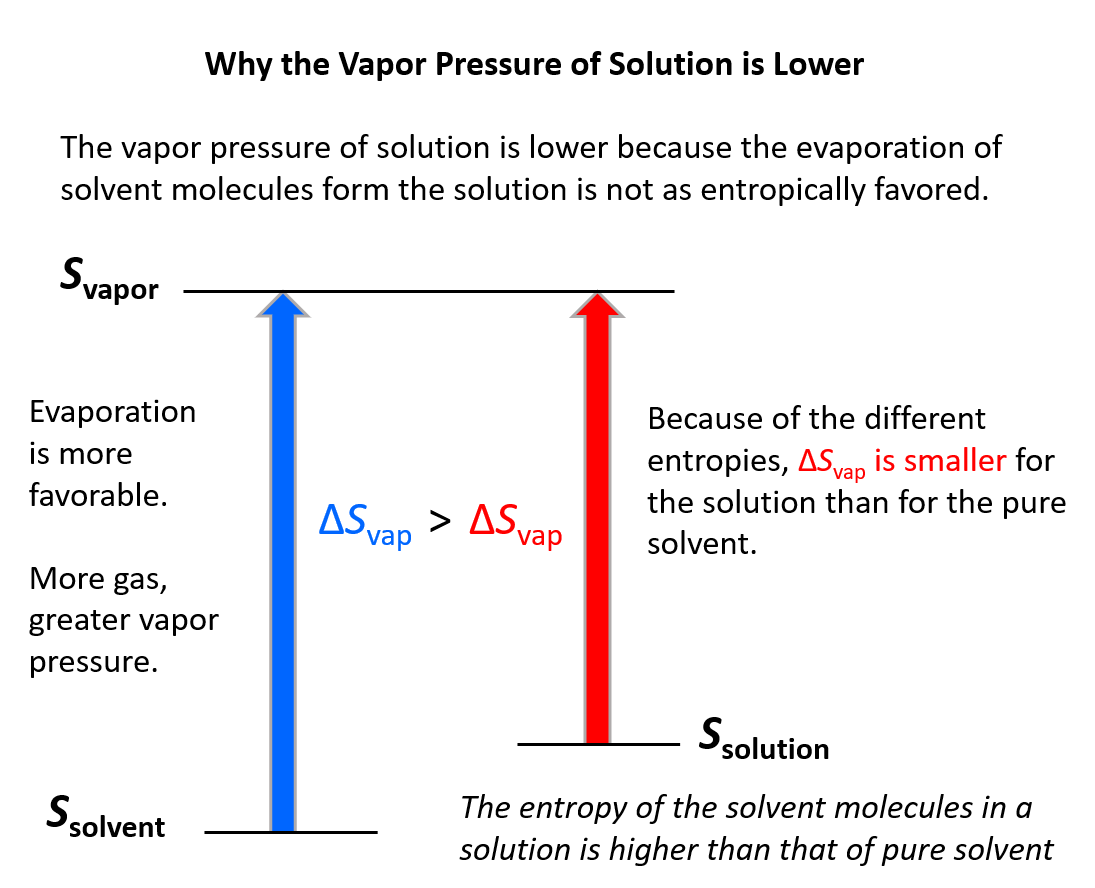
A more fundamental answer can be given using the principle of entropy. Remember, entropy increases with the randomness of the system, and therefore, it increases when solvent molecules evaporate because that is a transition from liquid to gas phase where the molecules have more freedom.
Now, when the solute and solvent are mixed the entropy of the system is already a little higher compared to the pure solvent. Consequently, the gain of entropy when solvent molecules evaporate is not as significant:
Calculating the Vapor Pressure Lowering
To calculate the vapor pressure lowering, we rely on the relationship between the vapor pressure of a solution (Psolution), the mole fraction of the solvent (Χsolvent), and the vapor pressure of the pure solvent (P°solvent). This is given by the Raoult’s Law:
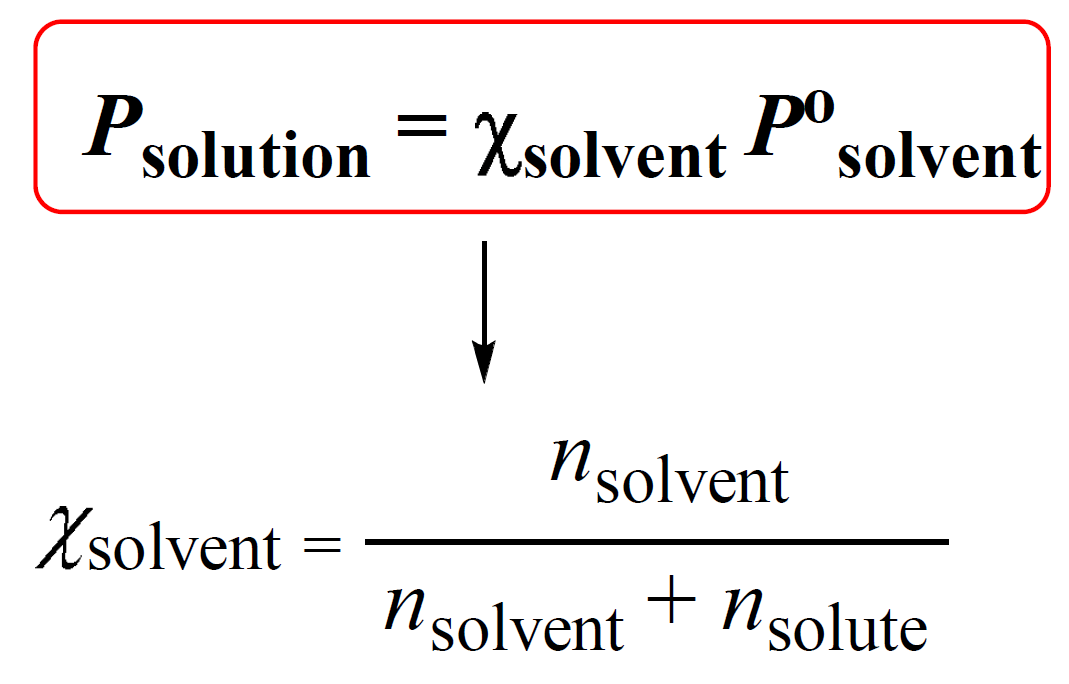
Χsolvent is the mole fraction of the solvent which is calculated as shown above.
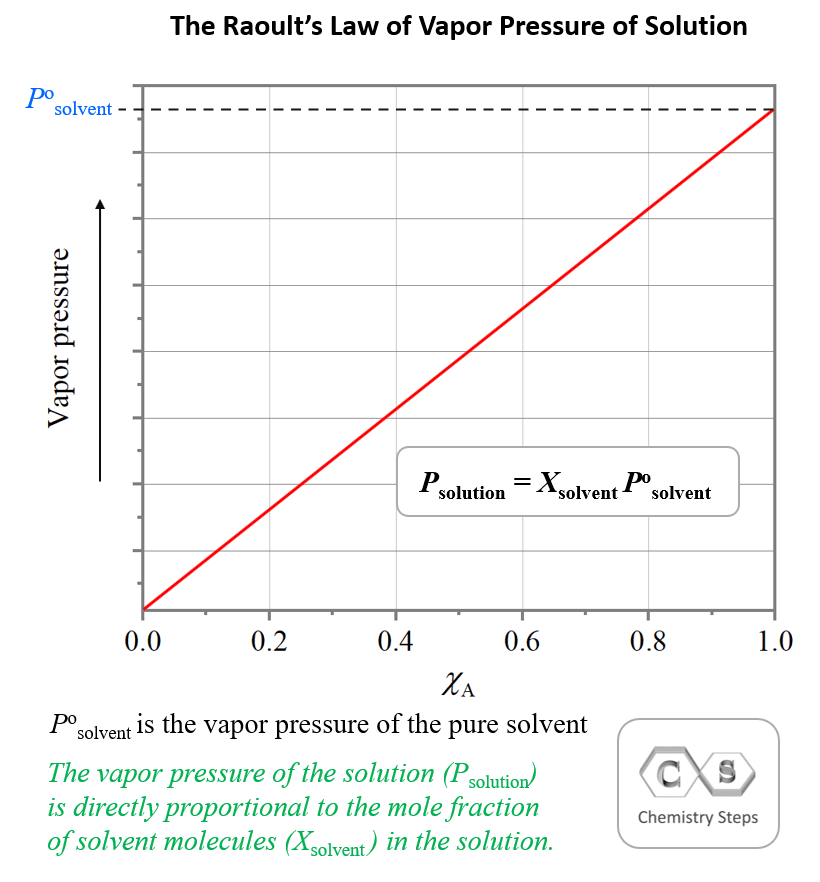
The essence of Raoult’s Law is that the more solvent we have in the solution, the greater the vapor pressure is going to be. This is because the only component of a solution containing a nonvolatile solute that contributes to the vapor pressure is the solvent. This correlation is given based on the mole fraction of the solvent – the vapor pressure of the solution is directly proportional to the mole fraction of solvent molecules in the solution:
For example, calculate the vapor pressure of a solution at 25°C that is made by adding 47.9 g of glucose (C6H12O6) to 340.0 mL of water. The vapor pressure of pure water at 25°C is 23.8 torr and the density of water is 1.00 g/mL.
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
Where Po (solvent) is the vapor pressure of pure solvent, P – the vapor pressure of the solution, Χ – the mole fraction of the solvent
We have the vapor pressure of pure water; Po (H2O) = 23.8 Torr, so the only missing part is the mole fraction of the solvent (water in this case) which is the ratio of the moles of solvent over the total moles of the solvent and the solute:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}}}{\rm{ }}\]
Determine the moles:
\[{\rm{}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{340}}{\rm{.0}}\,\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}{\rm{.00}}\,{\rm{g}}}}{{{\rm{1}}\,\cancel{{{\rm{mL}}}}}}\; = \,340.\;{\rm{g}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{340}}{\rm{.}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{8}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\; = \,18.9\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}\;{\rm{ = }}\,{\rm{47}}{\rm{.9}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{80}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.266}}\;{\rm{mol}}\]
The mole fraction is equal to:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{18}}{\rm{.9}}\,{\rm{mol}}}}{{\left( {{\rm{18}}{\rm{.9}}\;{\rm{ + }}\,{\rm{0}}{\rm{.266}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.986 }}\]
Therefore, the vapor pressure of the solution is:
Psolution = 0.986 x 23.8 torr = 23.5 torr
Vapor Pressure of Electrolyte Solutions
When defining the colligative properties, we said that they only depend on the number of solute particles. Now, let’s say we dissolve 1 mole of NaCl in water and need to measure the vapor pressure of the solution. The question is how many particles do we have in the solution?
Remember, NaCl is a strong electrolyte and dissociates into ions in aqueous solutions.
NaCl(aq) → Na+(aq) + Cl–(aq)
Therefore, the concentration of the solute particles is given by the Na+ and Cl– ions rather than the salt. So, if we need to calculate the mole fraction of the solvent, we need to multiply the moles of NaCl by two.
For example, a solution is prepared by dissolving 0.248 mol of NaCl in 1.85 mol of H2O. Calculate the vapor pressure of the solution at 40 °C. The vapor pressure of pure water at 40 °C is 55.0 torr.
The key part in solving problems with electrolytes is to remember that they dissociate into ions and because the colligative properties depend on the number of dissolved particles, we need to use the moles of the ions and not the salt.
For example, NaCl dissociates in two ions:
NaCl(aq) →Na+(aq) + Cl–(aq)
Therefore, the number of moles for the particles is 2 x 0.248 = 0.496 mol.
The number of ions is usually given by the van’t Hoff factor which is close to the number of ions produced upon the dissociation. So, in this case, it should be about 2. If the van’t Hoff factor is not given, we usually assume it based on the number of ions.
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
We have the vapor pressure of pure water; Po (H2O) = 55.0 Torr, so the only missing part is the mole fraction of the solvent (water in this case) which is the ratio of the moles of solvent over the total moles of the solvent and the solute:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,2{\rm{n}}\,{\rm{(NaCl)}}}}{\rm{ }}\]
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{1}}{\rm{.85}}\,{\rm{mol}}}}{{\left( {{\rm{1}}{\rm{.85}}\;{\rm{ + }}\,{\rm{2}}\,{\rm{x 0}}{\rm{.248}}} \right)\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.78857}}\;{\rm{ }}\]
Psolution = 0.78857 x 55.0 torr = 43.4 torr
In general, we can calculate the number of ions based on the formula of the salt. For example, 1 mole of MgBr2 is expected to produce 3 moles of ions because each formula unit contains one Mg2+ and 2 Br– ions. However, the dissociation of most ionic compounds does not occur at 100%, and the solution of an ionic compound usually contains fewer particles than what its formula suggests. The actual extent of dissociation can be expressed as a van’t Hoff factor (i).
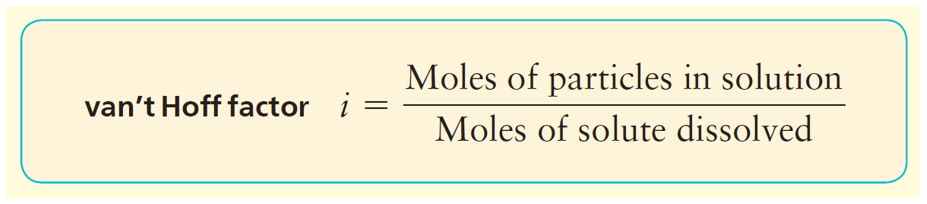
For most ionic compounds, the van’t Hoff’s constant is determined experimentally, and will likely be given to you in the test. If it is not, and there is nothing mentioned about, you can go based on the formula of the compound. For nonelectrolytes, it is assumed to be 1 as we do not worry about their negligible dissociation.
Vapor Pressure of Solutions Containing a Volatile Solute
Some solutions contain a volatile solute that evaporates and therefore, contributes to the vapor pressure of the solution. So, how do we calculate the vapor pressure of such solutions?
Remember from the gases chapter that the total pressure of an ideal gas mixture is equal to the sum of the pressures that each gas would exert if it were present alone:
PTotal = PA + PB
This is known as the Dalton’s law of partial pressures, and it is applicable to the vapor pressure of a solution containing two volatile liquids. If the liquids in the solution behave ideally, meaning their intermolecular interactions are comparable to those of intramolecular interactions, then we should be able to calculate the vapor pressure of each component, and add them up to determine total vapor pressure using their mole fractions:
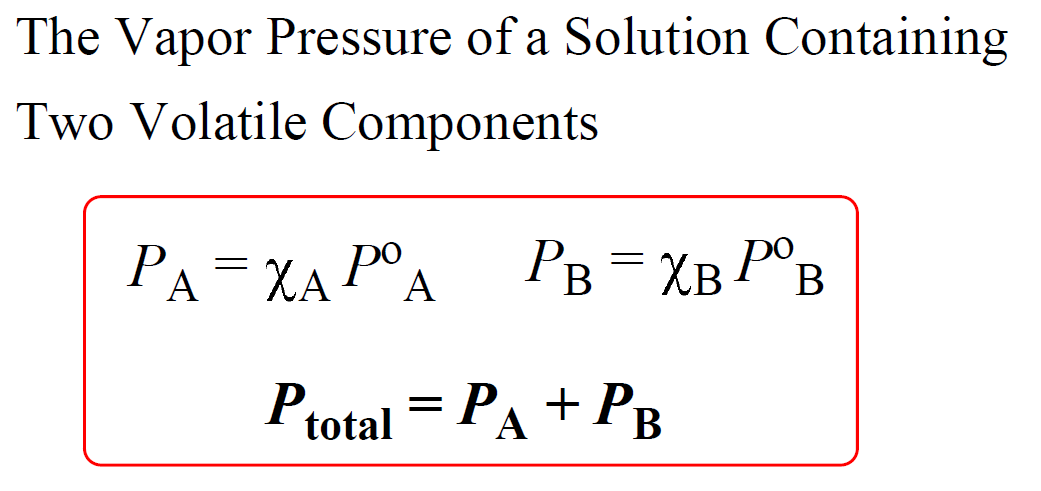
For example, let’s calculate the total vapor pressure of a mixture containing two similar organic liquids benzene, C6H6 and toluene, C7H8 in a 1:1 mole ratio. The vapor pressure of pure benzene is P° = 96.0 mm Hg at 25 °C, and that of pure toluene is P° = 30.3 mm Hg.
The total vapor pressure is calculated with the formula:
Ptotal = (Χbenzene) (Pobenzene) + (Χtoluene) (Potoluene)
Ptotal = 0.5 x 96.0 mmHg + 0.5 x 30.3 mmHg = 63.2 mmHg
To determine whether the solution is ideal or not, the calculated value of the total vapor pressure is compared with the experimental data. In this case, the values are identical, and therefore, the solution is said to be ideal.
A graph showing the dependence of the total vapor pressure on the mole fraction and the vapor pressure of each component typically looks like this:
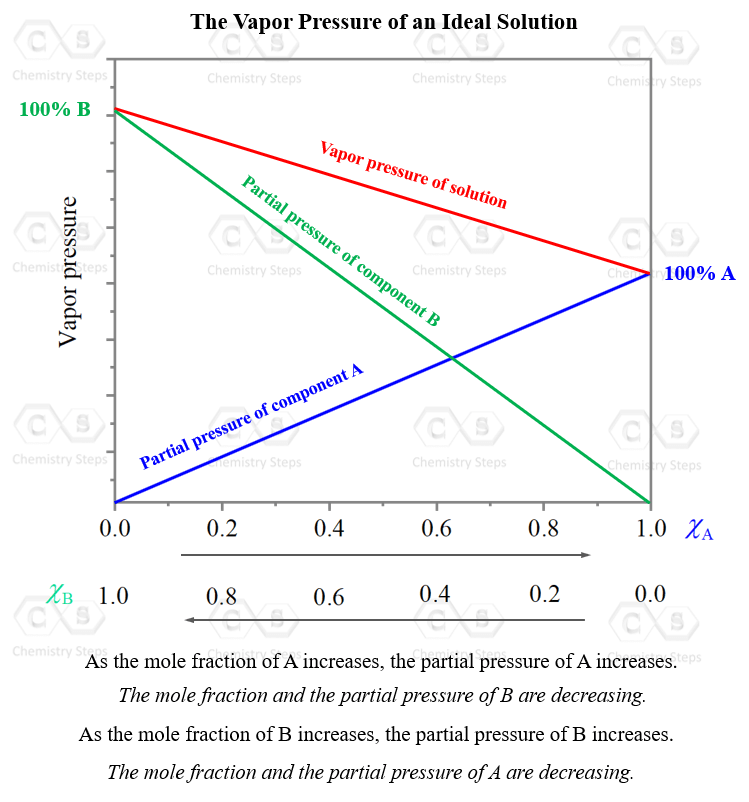
As the mole fraction, and the partial pressure of one component are increasing, those of the other component are decreasing. What is unique, and expected, for an ideal solution, is that at any mole ratio (x axis), the total pressure is the sum of the partial pressure of the two components. So, they are just mathematically added:

The same graph for a nonideal mixture does not show a linear dependence of the total pressure on the mole ratio and the partial pressure of the volatile components.
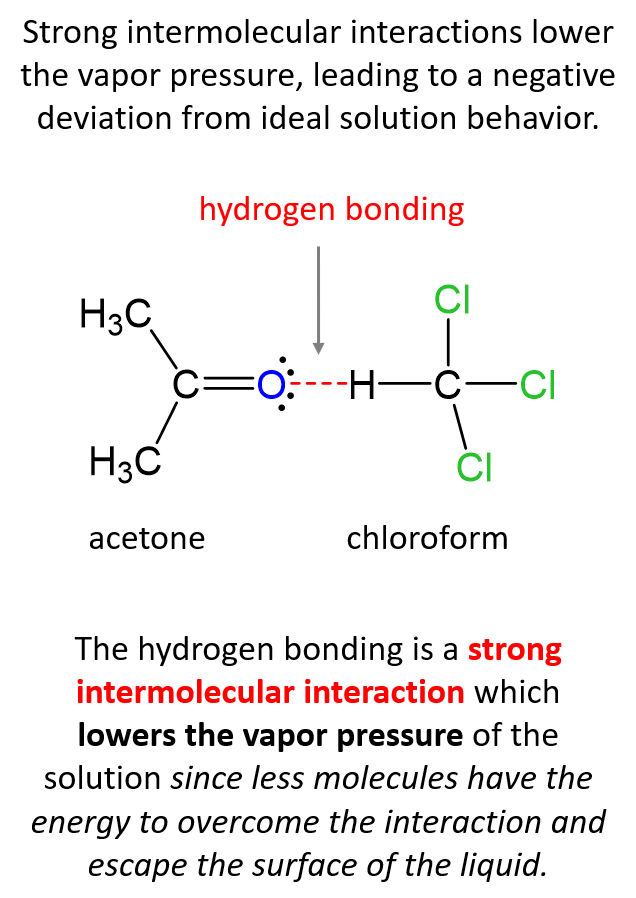
For example, the mixture of acetone, C3H6O and chloroform, CHCl3 shows a negative deviation from ideal behavior. The total vapor pressure is smaller than the sum of the calculated partial pressures of the components.
A typical graph for such behavior would look like this:
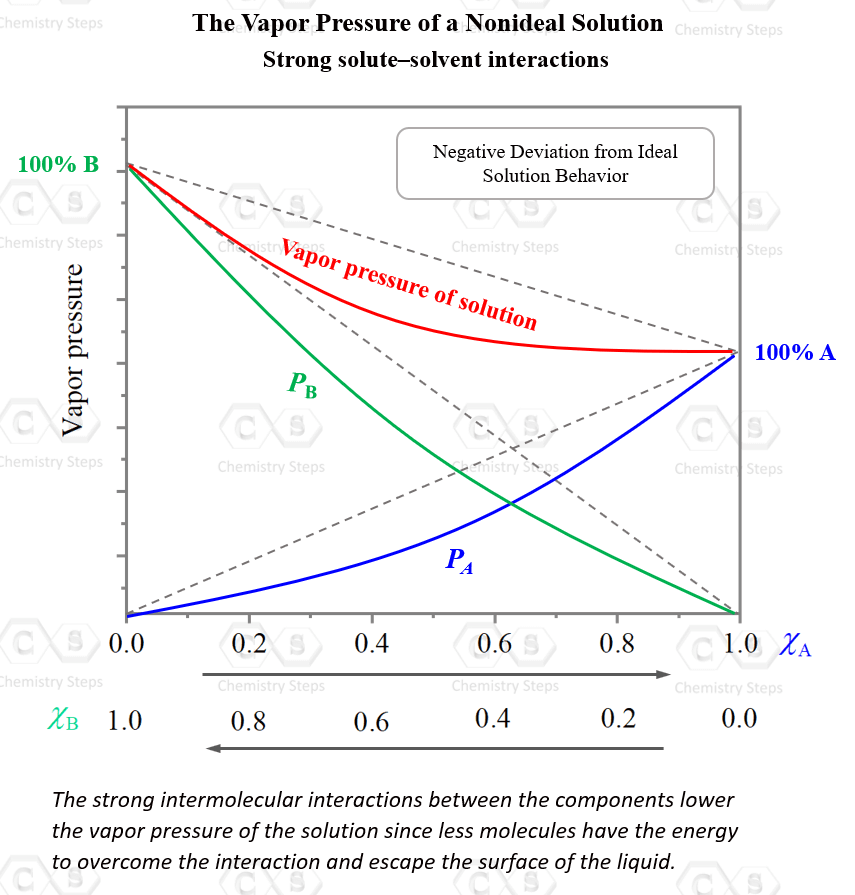
So, why is the solution of chloroform and acetone is not ideal?
The reason for this is the strong intermolecular interactions between the chloroform and acetone molecules. Hydrogen bonding is a strong intermolecular interaction, and it lowers the vapor pressure of the solution since less molecules have the energy to overcome the interaction and escape the surface of the liquid.
On the other hand, if the solute-solvent interactions are weaker than solvent–solvent interactions, it is easier for the molecules to evaporate which leads to a higher total pressure than predicted by Raoult’s law:
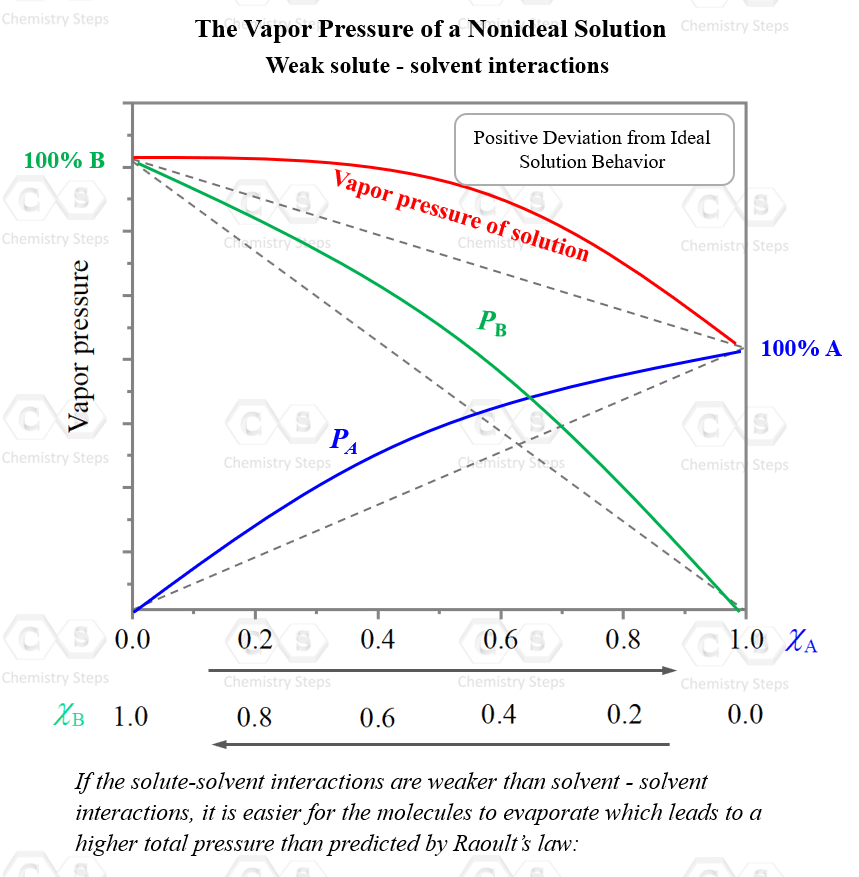
The higher the concentration of the solute, the more noticeable this effect will be.
Check Also
- Colligative Properties
- Boiling Point Elevation
- Freezing Point Depression
- Osmotic Pressure
- Molarity, Molality, and Other Concentrations – Practice Problems
- Colligative Properties Practice Problems
Practice
Calculate the vapor pressure of a solution prepared by adding 128 g glycerin (C3H8O3) to 421 g of water at 35.0 oC. Assume that the vapor pressure of pure water at this temperature is 42.2 torr and glycerin is a nonvolatile and nonelectrolyte liquid.
Calculate the vapor pressure and the vapor pressure lowering of the solution at 25°C prepared by dissolving 26.7 g of sucrose, C12H22O11, in 85.0 g of water. The vapor pressure of pure water at 25°C is 23.8 torr.
How many grams of urea (NH2)2CO) must be added to 485 g of water to prepare a solution with a vapor pressure of 22.0 torr at 25 oC? The vapor pressure of water at 25 °C is 23.8 torr.
The vapor pressure of a solution containing 60.0 g naphthalene (C10H8) in 245 g benzene (C6H6) is 130. torr at 35 oC. Calculate the vapor pressure of pure benzene at this temperature considering that naphthalene is a nonelectrolyte solid.
Determine the mole fraction of the solute in a solution of methanol with a vapor pressure of 675 torr at 64.7 °C which is the normal boiling point of methanol.
Determine the molar mass of a nonvolatile, nondissociating compound if adding 15.7 g of it to 92.0 g of ethanol (C2H5OH) has decreased the vapor pressure from 0.875 atm to 0.842 atm.
How many moles of a nonvolatile compound was added to 0.400 mol of benzene, C6H6 at 25°C if the resulting solution has a vapor pressure of 71.0 Torr? The vapor pressure of pure benzene at this temperature is 94.6 Torr.
A solution is prepared by mixing 4.23 g of chloroform (CHCl3) and 3.68 g of hexane (C6H14) at 25 °C. The vapor pressures of pure chloroform and pure hexane, at this temperature, are 197 torr and 154 torr, respectively. Assuming ideal behavior, calculate the total vapor pressure above the solution.
A solution contains a mixture of pentane, C5H12 and diethyl ether, (C2H5)2O. At a certain temperature, the vapor pressure of the solution is 438 torr. At this temperature, pure pentane and diethyl ether have vapor pressures of 362 torr and 512 torr, respectively. What is the mole fraction composition of the mixture assuming an ideal behavior?
A solution is prepared by mixing 5.81 g acetone, C3H6O and 11.9 g chloroform, CHCl3. Determine if this is an ideal solution given that at 35 °C the total vapor pressure is measured to be 260. torr. The vapor pressures of pure acetone and pure chloroform at 35 °C are 345 and 293 torr, respectively.
Calculate the vapor pressure of a solution prepared by dissolving 46.0 g of K2SO4 in 200. g water at 25 °C. The vapor pressure of pure water at 25 °C is 23.8 torr.
