Have you ever wondered what they are sparing on airplanes on cold days before they take off?

What they are spraying is a solution typically containing ethylene glycol, C₂H₆O₂ which lowers the freezing point of water. It is essentially the same solution that is used as antifreeze in cars.
This feature is called the freezing point depression and it is also a type of colligative properties. The freezing point of the solution is generally lower than that of the solvent.
We can also see this in the phase diagram of the solvent and the solution. It includes two regions of interest for the colligative properties. On the left side, is the freezing/melting point region, and on the right side, toward higher temperatures, we have the boiling point region. We have already discussed the boiling point elevation of the solution, so let’s now see how the freezing point depression is explained.
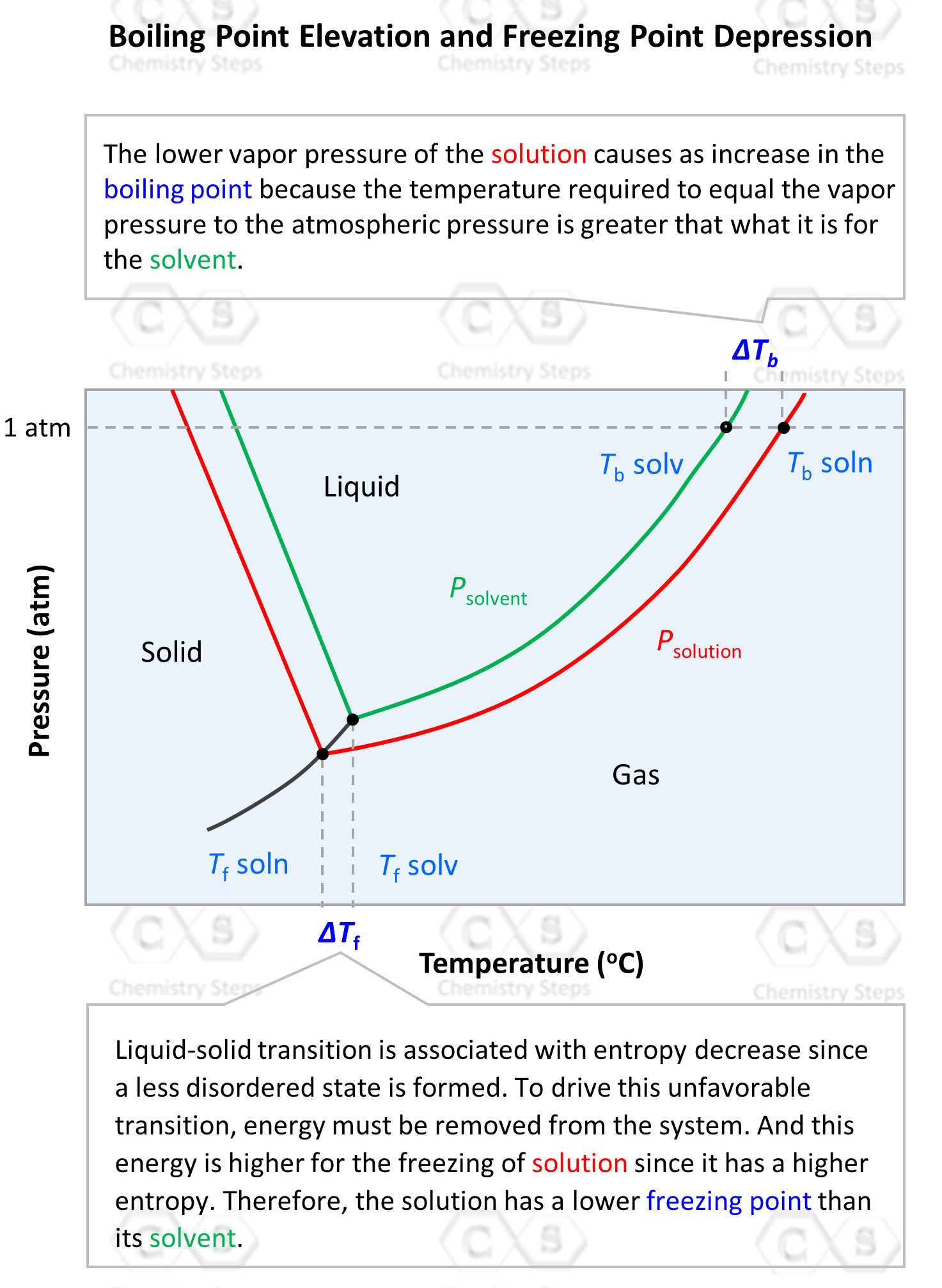
On the x axis, we have the temperature and as it increases, the phase is transitioning from solid-liquid-gas. Notice, on the left side, that the freezing point of the solution is lower than that of the solvent.
To understand this property, let’s again recall that the entropy of a solution is higher than the entropy of the solvent because the mixing of components increases the randomness of the system.
Freezing, on the other hand, decreases the randomness, and thus the process requires energy to be removed from the system to create a more ordered state. Now, because the solution has higher entropy, it requires more energy to be removed to transition to a solid phase. Therefore, a solution has a lower freezing point than the solvent.
Calculating the Freezing Point Depression
The Freezing point depression is calculated with the following formula:
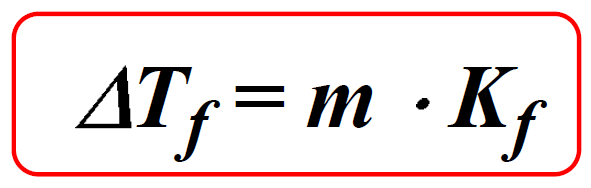
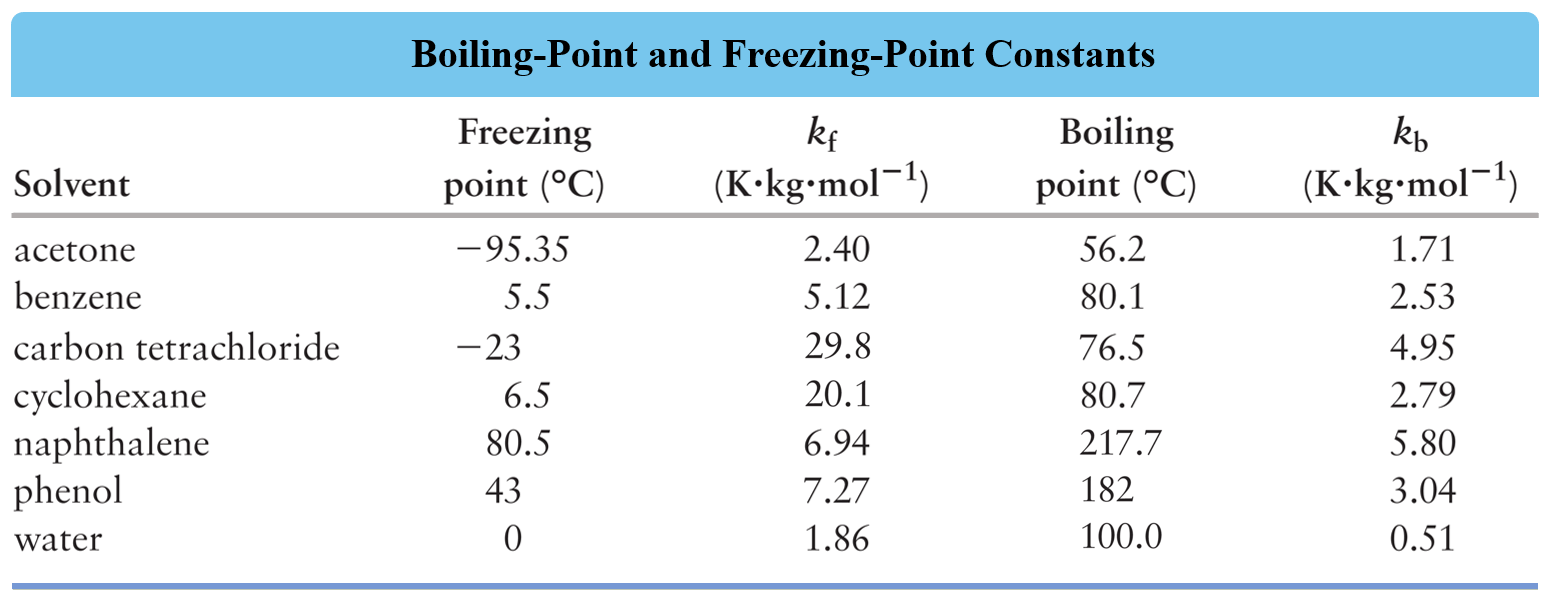
Where Kf is the molal freezing point depression constant characteristic of a given solvent. The values of Kf for some common solvents are given below:
and m is the molality of the solute which is calculated using this formula:
For example, using the appropriate data in the table, determine the freezing point depression of the solution that contains 24.1 g urea (NH2)2CO) in 485 mL of water.
The freezing point depression is calculated by the following formula:
ΔTf = m x Kf
Kf is the freezing point depression constant for the solvent, and from the table, we find that it is 1.86 oC/m
m is the molality of the solute which is equal to:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{mol}}\;{\rm{(solute)}}}}{{{\rm{kg}}\,{\rm{(solvent)}}}}\]
The moles of urea are calculated from the mass:
\[{\rm{n}}\,{\left( {{\rm{N}}{{\rm{H}}_{\rm{2}}}} \right)_{\rm{2}}}{\rm{CO)}}\;{\rm{ = }}\,{\rm{24}}{\rm{.1}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{60}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.401}}\;{\rm{mol}}\]
Convert the mL to kg for water:
\[{\rm{m}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{485}}\,\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}{\rm{.00}}\,\cancel{{\rm{g}}}}}{{{\rm{1}}\,\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{kg}}}}{{{\rm{1000}}\;\cancel{{\rm{g}}}}}{\rm{ = }}\,{\rm{0}}{\rm{.485}}\,{\rm{kg}}\]
The molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.401}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.485}}\,{\rm{kg}}}}\; = \;0.827\,m\]
The freezing point depression would then be:
ΔTf = Kfm = 1.86 oC /m x 0.827 m = 0.902 oC
The Freezing Point Depression of Electrolyte Solutions
As in the case of vapor pressure lowering, when a strong electrolyte is dissolved in water, the concentration of the solute particles is given by the ions rather than the formula of the compound because strong electrolytes dissociate into ions in aqueous solutions.
So, if we dissolve 1 mole of NaCl in water it will dissociate into ions and two moles of ions will be formed:
NaCl(aq) → Na+(aq) + Cl–(aq)
In general, we can calculate the number of ions based on the formula of the salt. For example, 1 mole of MgBr2 is expected to produce 3 moles of ions because each formula unit contains one Mg2+ and 2 Br– ions. However, the dissociation of most ionic compounds does not occur at 100%, and the solution of an ionic compound usually contains fewer particles than what its formula suggests. The actual extent of dissociation can be expressed as a van’t Hoff factor (i).
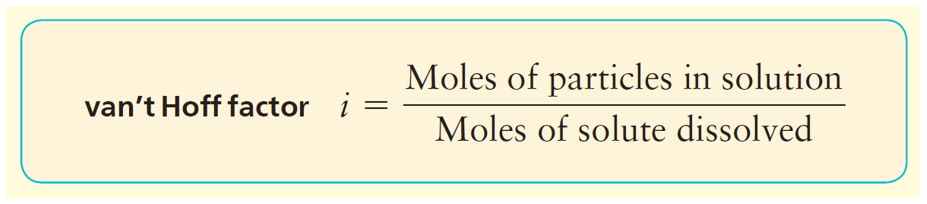
For most ionic compounds, the van’t Hoff’s constant is determined experimentally, and will likely be given to you in the test. If it is not, and there is nothing mentioned about, you can go based on the formula of the compound. For nonelectrolytes, it is assumed to be 1 as we do not worry about their negligible dissociation.
For example, calculate the freezing point of the solution prepared by dissolving 4.80 g NaCl in 25.0 g of water.
The freezing point depression is calculated by the following formula:
ΔTf = m x Kf
Kf is the freezing point depression constant for the solvent, and from the table, we find that it is 1.86 oC/m
m is the molality of the solute which is equal to:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{mol}}\;{\rm{(solute)}}}}{{{\rm{kg}}\,{\rm{(solvent)}}}}\]
The moles of particles from 4.80 g NaCl are calculated by multiplying the moles of NaCl by two since it dissociates into two ions:
\[{\rm{n}}\,({\rm{particles)}}\;{\rm{ = }}\,2\,{\rm{ \times }}\;{\rm{4}}{\rm{.80}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{58}}{\rm{.44}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.164}}\;{\rm{mol}}\]
The mass of water is 0.0250 kg, therefore, the molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.164}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.0250}}\,{\rm{kg}}}}\; = \;6.56\,m\]
The freezing point depression would then be:
ΔTf = Kfm = 1.86 oC /m x 6.56 m = 12.2 oC
The normal freezing point of water is 0oC, therefore, the freeing point of the solution will be:
0 – 12.2 = -12.2 oC
For more practice problems on the colligative properties, follow this link.
Check Also
- Colligative Properties
- Vapor Pressure Lowering
- Boiling Point Elevation
- Osmotic Pressure
- Molarity, Molality, and Other Concentrations – Practice Problems
- Colligative Properties Practice Problems
Practice
Determine the freezing point of a solution containing 1.80 g of glycerol, C3H8O3, in 26.0 g of water.
A solution is prepared by dissolving 75.0 g glycerin (C3H8O3) in 240. g water. Calculate the boiling point of the solution. Glycerin is a nonelectrolyte.
A 1.60 g sample of a newly synthesized supplement was dissolved in 12.0 g carbon tetrachloride, CCl4. The boiling point of this solution was determined to be 79.2 oC while the boiling point of pure carbon tetrachloride is 76.5 oC. Calculate the molar mass of the supplement considering that is a nonelectrolyte.
A 12.4 g of an unknown nonelectrolyte was dissolved in 100.0 g of water to prepare a solution with a freezing point of -1.7 °C. Calculate the molar mass of the unknown compound.
How many grams of ethylene glycol (C2H6O2), a nonelectrolyte, must be added to 5.40 L water to prepare an antifreeze solution with a freezing point of -30.0 oC?
A sample of 23.0 g naphthalene (C10H8) was added to benzene (C6H6) and the resulting solution had a boiling point of 83.7 oC. How many liters of benzene were used to prepare the solution if the normal boiling point of benzene is 80.1 oC and the density is 0.877 g/mL?
You are planning a winter trip and you have an antifreeze solution that is 40.0 % by mass of ethylene glycol (C2H6O2) in water. Would this antifreeze be good enough for the trip considering that the temperature goes down as far as -30.0 °C? Ethylene glycol is a nonelectrolyte.
Calculate the boiling point of the solution prepared by dissolving 5.4 g FeCl3 in 36.0 g of water.
How many grams of NaCl were added to 1.00 L of water if the resulting solution has a freezing point of -7.40 °C? The density of water is 1.00 g/mL.
