In the previous post, we have seen that solutions have lower vapor pressure than the corresponding pure solvents. In short, this is because the solution has higher entropy than the solvent, and the evaporation of the solvent molecules from the solution does not gain as much entropy as it happens when solvent molecules evaporate from their pure liquid state:
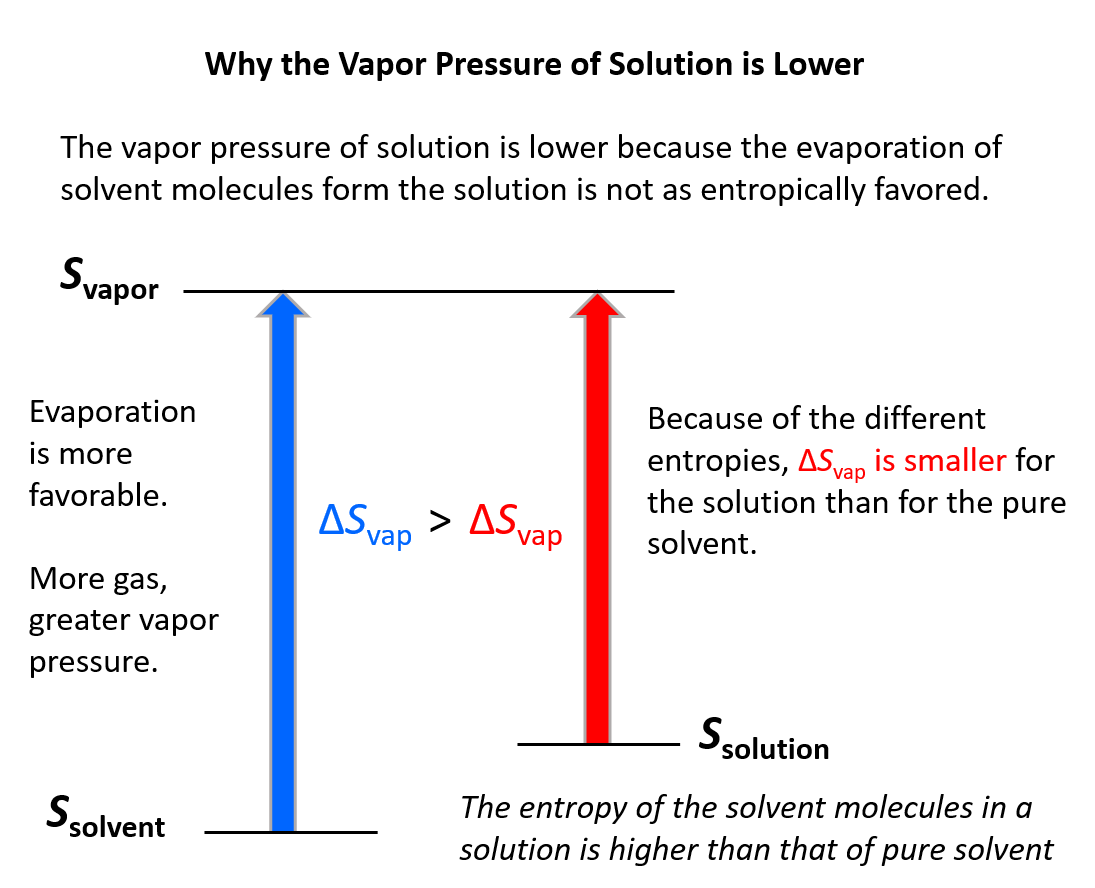
Now, because the solvent molecules have “a hard time” evaporating from the solution, the boiling point of the solution is higher than that of the solvent. Remember, the boiling point is reached when the vapor pressure of the liquid equals the external pressure. So, if the vapor pressure is lower, then it will take a higher temperature to bring it to the level of the external pressure.
We can also see this in the phase diagram of the solvent and the solution. It includes two regions of interest for the colligative properties. On the left side, is the freezing/melting point region, and on the right side, toward higher temperatures, we have the boiling point region:
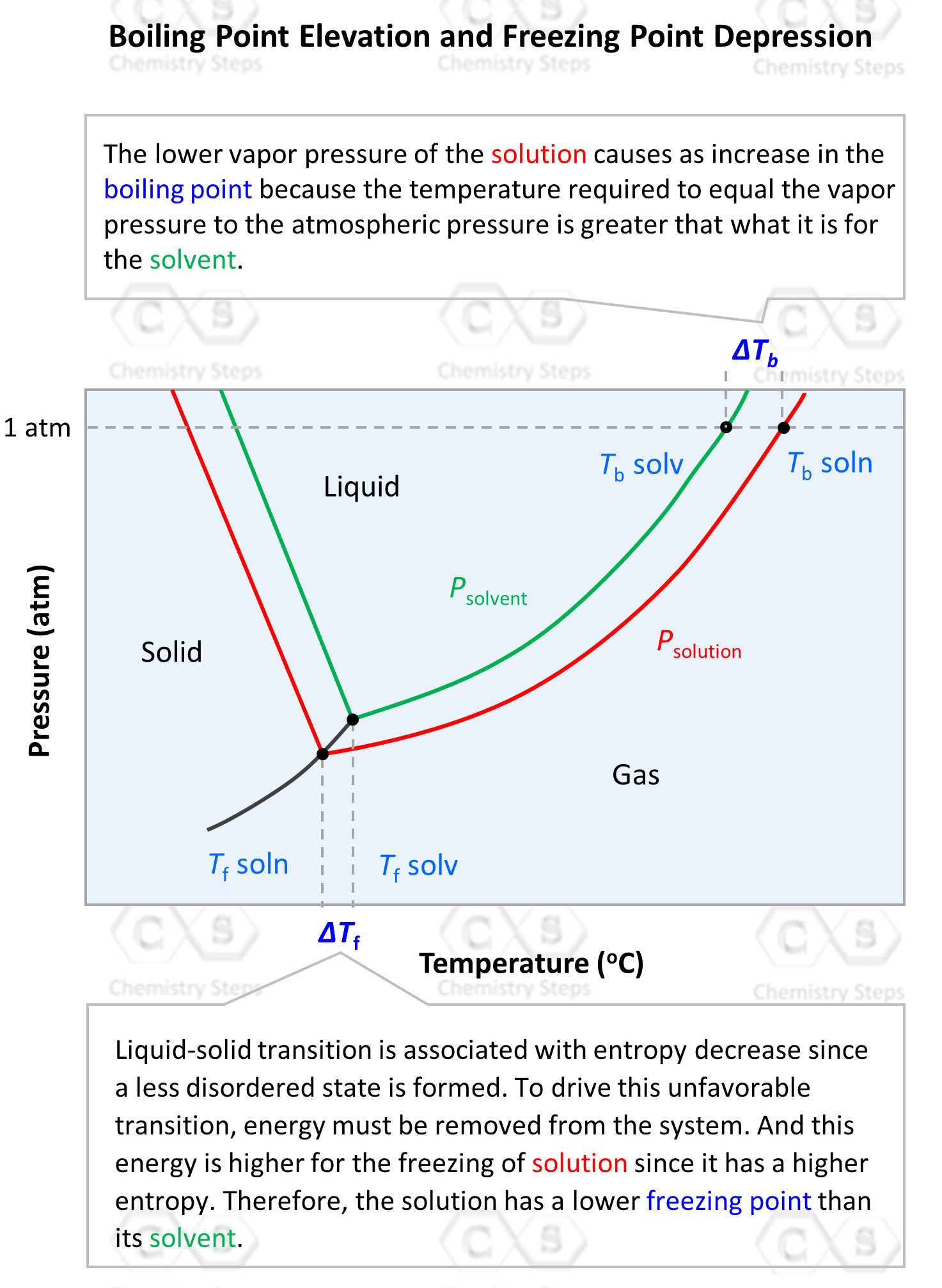
On the x axis, we have the temperature and as it increases, the phase is transitioning from solid-liquid-gas therefore, we find the boiling point of the solution and the solvent on the upper right side. What shows the difference in boiling points of the solvent and the solution is that the line for the solution lies lower and stretches farther to the right, indicating a higher temperature.
On the left side, we have the freezing points of the solvent and solution. Notice that the freezing point of the solution is lower than that of the solvent, and this is the next colligative property called freezing point depression. We will cover this in a separate post, but for now, let’s see how the boiling point elevation, ΔTb is calculated.
Calculating the Boiling Point Elevation
The boiling point elevation is calculated with the following formula:
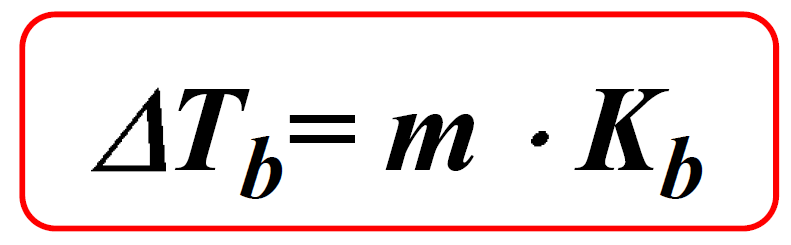
Where Kb is the molal boiling-point-elevation constant characteristic of a given solvent. The values of Kb for some common solvents are given below:

m is the molality of the solute which is calculated using this formula:
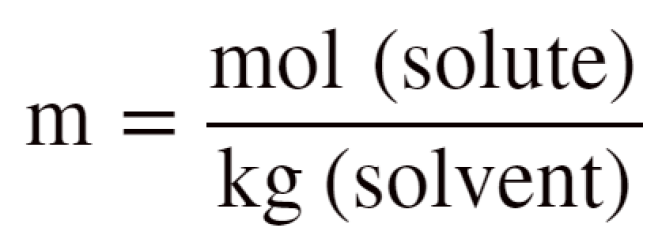
For example, a solution is prepared by dissolving 75.0 g glycerin (C3H8O3) in 240. g water. Calculate the boiling point of the solution. Glycerin is a nonelectrolyte.
The normal boiling point of water is 100 oC. So, to find the boiling point of the solution, we first calculate the boiling point elevation and add that to 100 oC.
For the boiling point elevation, we use a similar formula with a different constant:
ΔTb = Kbm
To find the molality, m, we need to moles of the solute and mass of the solvent in kg. 240. g of water is 0.240 kg.
The moles of glycerin are calculated from the mass:
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{75}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{92}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.814}}\;{\rm{mol}}\]
The molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.814}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.240}}\,{\rm{kg}}}}\; = \;3.393\,m\]
ΔTb = Kbm = 0.512 oC /m x 3.393 m = 1.74 oC
The boiling point of the solution would then be 100 + 1.74 = 101.74 oC
The Boiling Point Elevation of Electrolyte Solutions
As in the case of vapor pressure lowering, When a strong electrolyte is dissolved in water, the concentration of the solute particles is given by the ions rather than the formula of the compound because strong electrolytes dissociate into ions in aqueous solutions.
So, if we dissolve 1 mole of NaCl in water it will dissociate into ions and two moles of ions will be formed:
NaCl(aq) → Na+(aq) + Cl–(aq)
In general, we can calculate the number of ions based on the formula of the salt. For example, 1 mole of MgBr2 is expected to produce 3 moles of ions because each formula unit contains one Mg2+ and 2 Br– ions. However, the dissociation of most ionic compounds does not occur at 100%, and the solution of an ionic compound usually contains fewer particles than its formula suggests. The actual extent of dissociation can be expressed as a van’t Hoff factor (i).
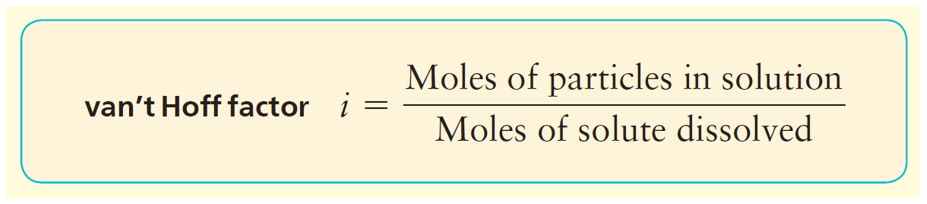
For most ionic compounds, the van’t Hoff’s constant is determined experimentally, and will likely be given to you in the test. If it is not, and there is nothing mentioned about it, you can go based on the formula of the compound. For nonelectrolytes, it is assumed to be 1 as we do not worry about their negligible dissociation.
For example, calculate the boiling point of the solution prepared by dissolving 5.4 g FeCl3 in 36.0 g of water.
The boiling point elevation is calculated by the following formula:
ΔTb = m x Kb
The moles of particles from 5.40 g FeCl3 are calculated by multiplying the moles of FeCl3 by four since it dissociates into four ions:
FeCl3(aq) →Fe3+(aq) + 3Cl–(aq)
\[{\rm{n}}\,({\rm{particles)}}\;{\rm{ = }}\,4\,{\rm{ \times }}\;{\rm{5}}{\rm{.40}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{162}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.133}}\;{\rm{mol}}\]
The mass of water is 0.0360 kg, therefore, the molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.133}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.0360}}\,{\rm{kg}}}}\; = \;3.69\,m\]
The boiling point elevation would then be:
ΔTb = Kbm = 0.512 oC /m x 3.69 m = 1.89 oC
The normal boiling point of water is 100 oC, therefore, the boiling point of the solution will be 101.89 oC ≈ 102 oC.
In the next article, we will discuss another colligative property which is the freezing point depression. For more practice problems on the colligative properties, follow this link.
Check Also
- Colligative Properties
- Vapor Pressure Lowering
- Freezing Point Depression
- Osmotic Pressure
- Molarity, Molality, and Other Concentrations – Practice Problems
- Colligative Properties Practice Problems
Practice
A 1.60 g sample of a newly synthesized supplement was dissolved in 12.0 g carbon tetrachloride, CCl4. The boiling point of this solution was determined to be 79.2 oC while the boiling point of pure carbon tetrachloride is 76.5 oC. Calculate the molar mass of the supplement considering that is a nonelectrolyte.
A sample of 23.0 g naphthalene (C10H8) was added to benzene (C6H6) and the resulting solution had a boiling point of 83.7 oC. How many liters of benzene were used to prepare the solution if the normal boiling point of benzene is 80.1 oC and the density is 0.877 g/mL?
