Practice problems on the colligative properties of solutions covering the freezing point depression, boiling point elevation, vapor pressure, and osmotic pressure of solutions prepared with nonelectrolytes as well as ionic compounds.
The links s for the corresponding topics are given herein:
Practice
Vapor Pressure Lowering
Calculate the vapor pressure of a solution at 25°C that is made by adding 47.9 g of glucose (C6H12O6) to 340.0 mL of water. The vapor pressure of pure water at 25°C is 23.8 torr and the density of water is 1.00 g/mL.
23.5 torr
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
Where Po (solvent) is the vapor pressure of pure solvent, P – the vapor pressure of the solution, Χ – the mole fraction of the solvent
We have the vapor pressure of pure water; Po (H2O) = 23.8 Torr, so the only missing part is the mole fraction of the solvent (water in this case) which is the ratio of the moles of solvent over the total moles of the solvent and the solute:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}}}{\rm{ }}\]
Determine the moles:
\[{\rm{}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{340}}{\rm{.0}}\,\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}{\rm{.00}}\,{\rm{g}}}}{{{\rm{1}}\,\cancel{{{\rm{mL}}}}}}\; = \,340.\;{\rm{g}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{340}}{\rm{.}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{8}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\; = \,18.9\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}\;{\rm{ = }}\,{\rm{47}}{\rm{.9}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{80}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.266}}\;{\rm{mol}}\]
The mole fraction is equal to:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{18}}{\rm{.9}}\,{\rm{mol}}}}{{\left( {{\rm{18}}{\rm{.9}}\;{\rm{ + }}\,{\rm{0}}{\rm{.266}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.986 }}\]
Therefore, the vapor pressure of the solution is:
Psolution = 0.986 x 23.8 torr = 23.5 torr
Calculate the vapor pressure of a solution prepared by adding 128 g glycerin (C3H8O3) to 421 g of water at 35.0 oC. Assume that the vapor pressure of pure water at this temperature is 42.2 torr and glycerin is a nonvolatile and nonelectrolyte liquid.
39.8 torr
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
Where Po (solvent) is the vapor pressure of pure solvent, P – the vapor pressure of the solution, Χ – the mole fraction of the solvent
We have the vapor pressure if pure water; Po (H2O) = 42.2 torr, so the only missing part is the mole fraction of the solvent (water in this case):
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}}}{\rm{ }}\]
Determine the moles:
\[{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{421}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{8}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\; = \,23.4\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{128}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{92}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{1}}{\rm{.39}}\;{\rm{mol}}\]
The mole fraction is equal to:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{23}}{\rm{.4}}\,{\rm{mol}}}}{{\left( {{\rm{23}}{\rm{.4}}\;{\rm{ + }}\,{\rm{1}}{\rm{.39}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.944 }}\]
Therefore, the vapor pressure of the solution is:
Psolution = 0.944 x 42.2 torr = 39.8 torr
Calculate the vapor pressure and the vapor pressure lowering of the solution at 25°C prepared by dissolving 26.7 g of sucrose, C12H22O11, in 85.0 g of water. The vapor pressure of pure water at 25°C is 23.8 torr.
Psolution = 23.4 torr
ΔP = 0.400 torr
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
We have the vapor pressure if pure water; Po (H2O) = 23.8 torr, so the only missing part is the mole fraction of the solvent (water in this case):
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,{\rm{n}}\,{\rm{(}}{{\rm{C}}_{{\rm{12}}}}{{\rm{H}}_{{\rm{22}}}}{{\rm{O}}_{{\rm{11}}}}{\rm{)}}}}{\rm{ }}\]
Determine the moles:
\[{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{85}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{8}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\; = \,4.72\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{{\rm{12}}}}{{\rm{H}}_{{\rm{22}}}}{{\rm{O}}_{{\rm{11}}}}{\rm{)}}\;{\rm{ = }}\,{\rm{26}}{\rm{.7}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{342}}{\rm{.3}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0780}}\;{\rm{mol}}\]
The mole fraction is equal to:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{4}}{\rm{.72}}\,{\rm{mol}}}}{{\left( {{\rm{4}}{\rm{.72}}\;{\rm{ + }}\,{\rm{0}}{\rm{.0780}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.984 }}\]
The vapor pressure of the solution is:
Psolution = 0.984 x 23.8 torr = 23.4 torr
Therefore, the vapor pressure has lowered by:
ΔP = 23.8 – 23.4 = 0.400 tor
How many grams of urea (NH2)2CO) must be added to 485 g of water to prepare a solution with a vapor pressure of 22.0 torr at 25 oC? The vapor pressure of water at 25 °C is 23.8 torr.
132 g
There are two approaches to solve this going wither based on the mole fraction of the solvent or the solute.
Approach 1 – using the mole fraction of the solvent
The plan here would be to assign x moles to urea in the expression for the mole fraction of water. For this, we write the formula for the vapor pressure of the solution like we did before:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
First, calculate the moles of water:
\[{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,4{\rm{85}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{8}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\; = \,26.9\;{\rm{mol}}\]
The mole fraction of water can be written as:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{26}}{\rm{.9}}\,}}{{{\rm{26}}{\rm{.9}}\;{\rm{ + }}\,{\rm{x}}}}\]
And now we can add this to the formula for the vapor pressure:
\[22.0\, = \;\left( {\frac{{{\rm{26}}{\rm{.9}}\,}}{{{\rm{26}}{\rm{.9}}\;{\rm{ + }}\,{\rm{x}}}}} \right)23.8\]
22.0 (26.9 + x) = 26.9 x 23.8
591.8 + 22.0x = 640.22
x = 2.20 moles
The molar mass of urea is 60.1 g/mol, therefore, the mass needed would be:
\[{\rm{m}}\;{\left( {{\rm{N}}{{\rm{H}}_{\rm{2}}}} \right)_{\rm{2}}}{\rm{CO)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.20}}\,{\rm{mol}}\,{\rm{ \times }}\,\frac{{{\rm{60}}{\rm{.1}}\,{\rm{g}}}}{{{\rm{1}}\,{\rm{mol}}}}\; = \;132\,{\rm{g}}\]
Alternatively, there is a formula that links the mole fraction of the solute with the difference between the vapor pressure of the solvent and the solution:
\[\Delta P\, = \;{\chi _{solute}}{P^o}_{solvent}\]
From this, we can calculate the mole fraction of urea:
\[{\chi _{urea}}\, = \;\frac{{\Delta P}}{{{P^o}_{water}}}\; = \;\frac{{23.8\, – 22.0}}{{23.8}}\; = \;0.07563\]
Assigning x mol for urea, its mole fraction would be:
\[{\chi _{{\rm{urea}}}}\;{\rm{ = }}\;\frac{{{\rm{x}}\,}}{{{\rm{26}}{\rm{.9}}\;{\rm{ + }}\,{\rm{x}}}}\; = \,0.07563\]
2.034 + 0.07563x = x
x = 2.20 moles
As expected, both approaches gave the same moles of urea, and therefore, the mass is also going to be the same.
The vapor pressure of a solution containing 60.0 g naphthalene (C10H8) in 245 g benzene (C6H6) is 130. torr at 35 oC. Calculate the vapor pressure of pure benzene at this temperature considering that naphthalene is a nonelectrolyte solid.
149 torr
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
The formula for the vapor pressure of pure solvent benzene would be:
\[{P^o}_{{\rm{benzene}}}\, = \;\frac{{{P_{{\rm{solution}}}}}}{{{\chi _{{\rm{benzene}}}}}}\]
To find the mole fraction of benzene, calculate the moles of both components.
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{{\rm{10}}}}{{\rm{H}}_{\rm{8}}}{\rm{)}}\;{\rm{ = }}\,{\rm{60}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{128}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.468}}\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{\rm{6}}}{\rm{)}}\;{\rm{ = }}\,{\rm{245}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{78}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{3}}{\rm{.14}}\;{\rm{mol}}\]
\[{\chi _{{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{\rm{6}}}}}\;{\rm{ = }}\;\frac{{{\rm{3}}{\rm{.14}}\,{\rm{mol}}}}{{\left( {{\rm{3}}{\rm{.14}}\;{\rm{ + }}\,{\rm{0}}{\rm{.468}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.870 }}\]
\[{P^o}_{{\rm{benzene}}}\, = \;\frac{{{P_{{\rm{solution}}}}}}{{{\chi _{{\rm{benzene}}}}}}\; = \;\frac{{{\rm{130}}{\rm{.}}\,{\rm{torr}}}}{{{\rm{0}}{\rm{.870}}}}\;{\rm{ = }}\;{\rm{149}}\,{\rm{torr}}\]
Determine the mole fraction of the solute in a solution of methanol with a vapor pressure of 675 torr at 64.7 °C which is the normal boiling point of methanol.
0.151
The normal boiling point of a compound is measured at 1 atm which corresponds to 760 torr. Therefore, Po = 760 torr at 64.7 oC, and Psolution at this temperature is 675 torr.
Using the formula for the vapor pressure of the solution, we can find the mole fraction of methanol, and subtracting that from one, we will have the mole fraction of the solute. Remember, that the sum of mole fractions is equal to one.
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
\[{\chi _{{\rm{methanol}}}}\, = \;\frac{{{P_{{\rm{solution}}}}}}{{{P^o}_{{\rm{methanol}}}}}\; = \;\frac{{675}}{{760}}\; = \,0.849\]
Therefore,
x (solute) = 1 – 0.849 = 0.151
Determine the molar mass of a nonvolatile, nondissociating compound if adding 15.7 g of it to 92.0 g of ethanol (C2H5OH) has decreased the vapor pressure from 0.875 atm to 0.842 atm.
200. g/mol
To determine the molar mass, we can first find the moles of the solute from the expression of the mole fraction. It can be either the mole fraction of the solvent or the solute when using the ΔP (see problem #4). In this case, we will use the mole fraction of the solvent.
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
First, calculate the moles of ethanol:
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH)}}\;{\rm{ = }}\,{\rm{92}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{46}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{2}}{\rm{.00}}\;{\rm{mol}}\]
Assigning x mol for the amount of the solute, the mole fraction of the ethanol can be written as:
\[{\chi _{{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}}}\;{\rm{ = }}\;\frac{{{\rm{2}}{\rm{.00}}\,}}{{{\rm{2}}{\rm{.00}}\;{\rm{ + }}\,{\rm{x}}}}\]
And now we can add this to the formula for the vapor pressure:
\[0.842\, = \;\left( {\frac{{{\rm{2}}{\rm{.00}}\,}}{{{\rm{2}}{\rm{.00}}\;{\rm{ + }}\,{\rm{x}}}}} \right)0.875\]
0.842 (2.00 + x) = 0.875 x 2.00
1.684 + 0.842x = 1.75
x = 0.07838 moles
The molar mass of the unknown can be calculated from the moles and the given mass:
M (solute) = 15.7 g ÷ 0.07838 mol = 200. g/mol
How many moles of a nonvolatile compound was added to 0.400 mol of benzene, C6H6 at 25°C if the resulting solution has a vapor pressure of 71.0 Torr? The vapor pressure of pure benzene at this temperature is 94.6 Torr.
0.133 mol
To determine the moles of the solute, we use the expression for the mole fraction. It can be either the mole fraction of the solvent or the solute when using the ΔP (see problem #4). In this case, we will use the mole fraction of the solvent.
We can assign x mol for the solute, and the mole fraction of the benzene can be written as:
\[{\chi _{{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{\rm{6}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.400}}\,}}{{{\rm{0}}{\rm{.400}}\;{\rm{ + }}\,{\rm{x}}}}\]
And now we can add this to the formula for the vapor pressure.
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
\[71.0\, = \;\left( {\frac{{{\rm{0}}{\rm{.400}}\,}}{{{\rm{0}}{\rm{.400}}\;{\rm{ + }}\,{\rm{x}}}}} \right)94.6\]
71.0 (0.400 + x) = 0.400 x 94.6
28.4 + 71.0x = 37.84
x = 0.133 moles
A solution is prepared by mixing 4.23 g of chloroform (CHCl3) and 3.68 g of hexane (C6H14) at 25 °C. The vapor pressures of pure chloroform and pure hexane, at this temperature, are 197 torr and 154 torr, respectively. Assuming ideal behavior, calculate the total vapor pressure above the solution.
173 torr
The vapor pressure of a solution containing two volatile components is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _A}{P^o}_A\; + \,{\chi _B}{P^o}_B\]
To determine the vapor pressure of the solution, we first calculate the moles and the mole fractions of the two liquids.
\[{\rm{n}}\,{\rm{(CHC}}{{\rm{l}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{4}}{\rm{.23}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{119}}{\rm{.4}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0354}}\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{14}}}}{\rm{)}}\;{\rm{ = }}\,{\rm{3}}{\rm{.68}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{86}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0427}}\;{\rm{mol}}\]
\[{\chi _{{\rm{CHC}}{{\rm{l}}_{\rm{3}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.0354}}\,{\rm{mol}}}}{{\left( {{\rm{0}}{\rm{.0354}}\;{\rm{ + }}\,{\rm{0}}{\rm{.0427}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.453 }}\]
\[{\chi _{{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{14}}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.0427}}\,{\rm{mol}}}}{{\left( {{\rm{0}}{\rm{.0354}}\;{\rm{ + }}\,{\rm{0}}{\rm{.0427}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.547 }}\]
You can also subtract the mole fraction of the first component from 1, as their sum must be equal to 1. And now, we can use the numbers to determine the vapor pressure of the solution:
\[{P_{solution}}\, = \;{\chi _{{\rm{CHC}}{{\rm{l}}_{\rm{3}}}}}{P^o}_{{\rm{CHC}}{{\rm{l}}_{\rm{3}}}}\; + \,{\chi _{{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{14}}}}}}{P^o}_{{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{14}}}}}\]
Psolution = 0.453 x 197 + 0.547 x 154 = 89.241 + 84.238 = 173 torr
A solution contains a mixture of pentane, C5H12 and diethyl ether, (C2H5)2O. At a certain temperature, the vapor pressure of the solution is 438 torr. At this temperature, pure pentane and diethyl ether have vapor pressures of 362 torr and 512 torr, respectively. What is the mole fraction composition of the mixture assuming an ideal behavior?
0.507
The vapor pressure of a solution containing two volatile components is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _A}{P^o}_A\; + \,{\chi _B}{P^o}_B\]
To determine the mole fractions of the liquids, we can assign x for C5H12, and 1 – x for (C2H5)2O. Remember, the sum of mole fractions of all the components is equal to one.
Psolution = x PoC5H12 + (1-x) Po(C2H5)2O = 438
Psolution = 362x + 512 (1-x) = 438
362x + 512 – 512x = 438
150x = 74
x = 0.493
Therefore, the mole fraction of C5H12 is 0.493, and that of (C2H5)2O is 0.507.
A solution is prepared by mixing 5.81 g acetone, C3H6O and 11.9 g chloroform, CHCl3. Determine if this is an ideal solution given that at 35 °C the total vapor pressure is measured to be 260. torr. The vapor pressures of pure acetone and pure chloroform at 35 °C are 345 and 293 torr, respectively.
The solution is not ideal.
The vapor pressure of a solution containing two volatile components is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _A}{P^o}_A\; + \,{\chi _B}{P^o}_B\]
To determine the vapor pressure of the solution, we first calculate the moles and the mole fractions of the two liquids.
\[{\rm{n}}\,{\rm{(CHC}}{{\rm{l}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{11}}{\rm{.9}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{119}}{\rm{.4}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0997}}\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{5}}{\rm{.81}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{58}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.100}}\;{\rm{mol}}\]
\[{\chi _{{\rm{CHC}}{{\rm{l}}_{\rm{3}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.0997}}\,{\rm{mol}}}}{{\left( {{\rm{0}}{\rm{.0997}}\;{\rm{ + }}\,{\rm{0}}{\rm{.100}}} \right)\,{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.499 }}\]
The mole fraction of acetone is therefore, 1 – 0.499 = 0.501. And now, we can use the numbers to determine the vapor pressure of the solution:
\[{P_{solution}}\, = \;{\chi _{{\rm{CHC}}{{\rm{l}}_{\rm{3}}}}}{P^o}_{{\rm{CHC}}{{\rm{l}}_{\rm{3}}}}\; + \,{\chi _{{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O}}}}{P^o}_{{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O}}}\]
Psolution = 0.499 x 293 + 0.501 x 345 = 146.207 + 172.845 = 319 torr
Because the observed vapor pressure is different than the calculated one, the solution is not ideal. The intermolecular forces between chloroform and acetone are stronger which decreases the vapor pressure of the mixture.
Freezing Point and Melting Point
Using the appropriate data in the table, determine the freezing point depression of the solution that contains 24.1 g urea (NH2)2CO) in 485 mL of water.
0.902 oC
The freezing point depression is calculated by the following formula:
ΔTf = m x Kf
Kf is the freezing point depression constant for the solvent, and from the table we find that it is 1.86 oC/m
m is the molality of the solute which is equal to:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{mol}}\;{\rm{(solute)}}}}{{{\rm{kg}}\,{\rm{(solvent)}}}}\]
The moles of urea are calculated from the mass:
\[{\rm{n}}\,{\left( {{\rm{N}}{{\rm{H}}_{\rm{2}}}} \right)_{\rm{2}}}{\rm{CO)}}\;{\rm{ = }}\,{\rm{24}}{\rm{.1}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{60}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.401}}\;{\rm{mol}}\]
Convert the mL to kg for water:
\[{\rm{m}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{485}}\,\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}{\rm{.00}}\,\cancel{{\rm{g}}}}}{{{\rm{1}}\,\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{kg}}}}{{{\rm{1000}}\;\cancel{{\rm{g}}}}}{\rm{ = }}\,{\rm{0}}{\rm{.485}}\,{\rm{kg}}\]
The molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.401}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.485}}\,{\rm{kg}}}}\; = \;0.827\,m\]
The freezing point depression would then be:
ΔTf = Kfm = 1.86 oC /m x 0.827 m = 0.902 oC
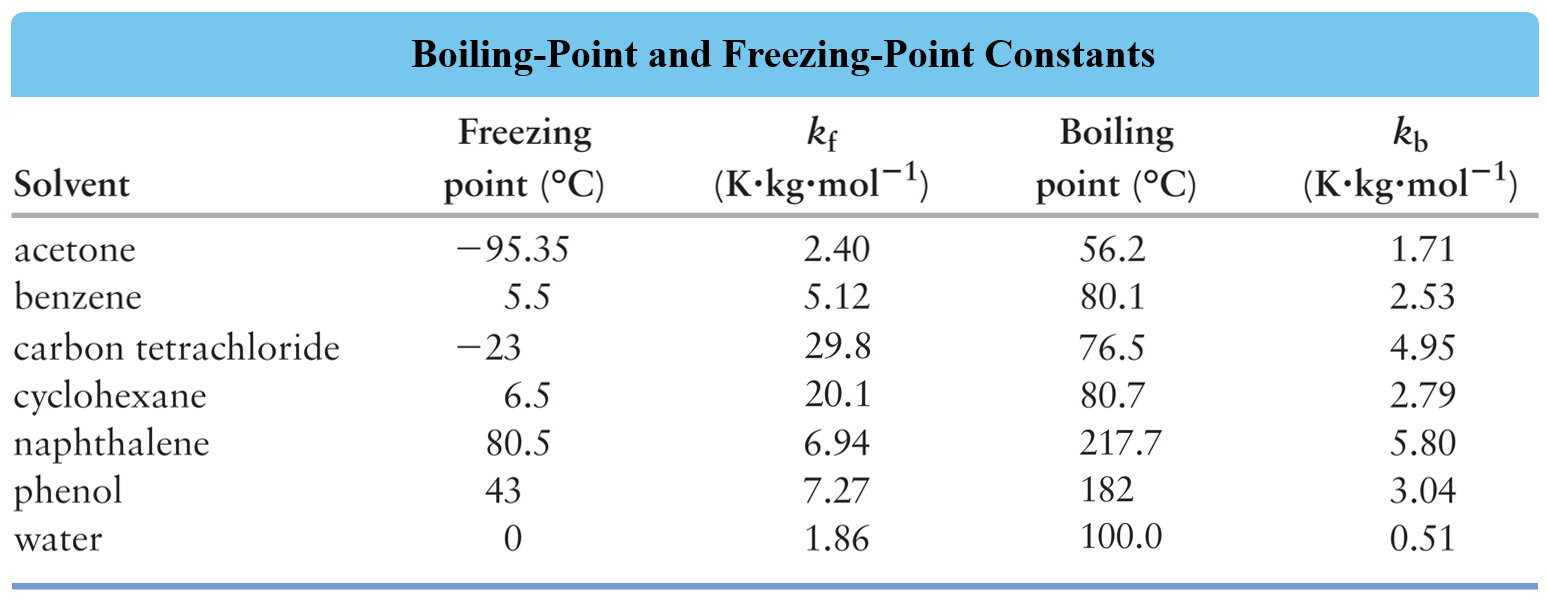
Determine the freezing point of a solution containing 1.80 g of glycerol, C3H8O3, in 26.0 g of water.
-1.40 oC
The freezing point depression is calculated by the following formula:
ΔTf = m x Kf
Kf is the freezing point depression constant for the solvent, and from the table, we find that it is 1.86 oC/m
m is the molality of the solute which is equal to:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{mol}}\;{\rm{(solute)}}}}{{{\rm{kg}}\,{\rm{(solvent)}}}}\]
The moles of glycerol are calculated from the mass:
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.180}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{92}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.00195}}\;{\rm{mol}}\]
The mass of water in kg is:
\[{\rm{m}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,{\rm{26}}{\rm{.0}}\,\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{kg}}}}{{{\rm{1000}}\;\cancel{{\rm{g}}}}}{\rm{ = }}\,{\rm{0}}{\rm{.0260}}\,{\rm{kg}}\]
The molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.0195}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.0260}}\,{\rm{kg}}}}\; = \;0.750\,m\]
The freezing point depression and the freezing point of the solution would then be:
ΔTf = Kfm = 1.86 oC /m x 0.750 m = 1.40 oC
Tf = 0 – 1.40 = -1.40 oC
A solution is prepared by dissolving 75.0 g glycerin (C3H8O3) in 240. g water. Calculate the boiling point of the solution. Glycerin is a nonelectrolyte.
101.74 oC
The normal boiling point of water is 100 oC. So, to find the boiling point of the solution, we first calculate the boiling point elevation and add that to 100 oC.
For the boiling point elevation, we use a similar formula with a different constant:
ΔTb = Kbm
To find the molality, m, we need to moles of the solute and mass of the solvent in kg. 240. g of water is 0.240 kg.
The moles of glycerin are calculated from the mass:
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{75}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{92}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.814}}\;{\rm{mol}}\]
The molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.814}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.240}}\,{\rm{kg}}}}\; = \;3.393\,m\]
ΔTb = Kbm = 0.512 oC /m x 3.393 m = 1.74 oC
The boiling point of the solution would then be 100 + 1.74 = 101.74 oC
A 1.60 g sample of a newly synthesized supplement was dissolved in 12.0 g carbon tetrachloride, CCl4. The boiling point of this solution was determined to be 79.2 oC while the boiling point of pure carbon tetrachloride is 76.5 oC. Calculate the molar mass of the supplement considering that is a nonelectrolyte.
244 g/mol
We are first going to determine the molality of the solution, from which the moles of the solute can be calculated based on the mass of the solvent. Once we know the moles, we can calculate the molar mass since the mass is also given.
ΔTb= 79.2 – 76.5 = 2.70 oC
The mass of carbon tetrachloride is 0.0120 kg, and the boiling point elevation constant for CCl4 is 4.95 oC/m.
The molality is derived from the expression of ΔTb:
\[m\, = \,\frac{{\Delta T}}{{{K_b}}}\; = \;\frac{{{\rm{2}}{\rm{.70}}}}{{{\rm{4}}{\rm{.95}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.5455}}\,{\rm{mol/kg}}\]
So, there are 0.5455 moles of solute in one kg of solvent. We need to find how many moles of solute we have in 0.0120 kg of solvent.
\[{\rm{n}}\,{\rm{(solute)}}\,{\rm{0}}{\rm{.0120}}\;\cancel{{{\rm{kg}}\;{\rm{solvent}}}}\;{\rm{ \times }}\;\frac{{{\rm{0}}{\rm{.5455}}\,{\rm{mol}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}\;{\rm{solvent}}}}}}{\rm{ = }}\,0.00655\,{\rm{mol}}\]
The given mass of the supplement was 1.60 g, therefore, the molar mass of it would be:
1.60 g ÷ 0.00655 mol = 244 g/mol
A 12.4 g of an unknown nonelectrolyte was dissolved in 100.0 g of water to prepare a solution with a freezing point of -1.7 °C. Calculate the molar mass of the unknown compound.
136 g/mol
We are going to first determine the molality of the solution, from which the moles of the solute can be calculated based on the mass of the solvent. Once we know the moles, we can calculate the molar mass since the mass is also given.
ΔTf= 0 – (-1.7) = 1.70 oC
The mass of the water is 0.1000 kg, and the freezing point depression constant for water is 1.86 oC/m.
The molality is derived from the expression of ΔTf:
\[m\, = \,\frac{{\Delta T}}{{{K_f}}}\; = \;\frac{{{\rm{1}}{\rm{.70}}}}{{{\rm{1}}{\rm{.86}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.914}}\,{\rm{mol/kg}}\]
So, there are 0.914 moles of solute in one kg of water. We need to find how many moles of solute we have in 0.1000 kg of water.
\[{\rm{n}}\,{\rm{(solute)}}\,{\rm{0}}{\rm{.1000}}\;\cancel{{{\rm{kg}}\;{\rm{solvent}}}}\;{\rm{ \times }}\;\frac{{{\rm{0}}{\rm{.914}}\,{\rm{mol}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}\;{\rm{solvent}}}}}}{\rm{ = }}\,0.0914\,{\rm{mol}}\]
The given mass of the unknown was 12.4 g, therefore, the molar mass of it would be:
12.4 g ÷ 0.0914 mol = 136 g/mol
How many grams of ethylene glycol (C2H6O2), a nonelectrolyte, must be added to 5.40 L water to prepare an antifreeze solution with a freezing point of -30.0 oC?
5.40 x 103 g
The mass of ethylene glycol can be determined from its moles which are calculated from the molality. The molality can be found from the expression for the freezing point depression. The normal freezing point of water is 0 oC, therefore, ΔTf= 30.0 oC. Based on these, the molality is:
\[m\, = \,\frac{{\Delta T}}{{{K_f}}}\; = \;\frac{{{\rm{30}}{\rm{.0}}}}{{{\rm{1}}{\rm{.86}}}}\,{\rm{ = }}\,{\rm{16}}{\rm{.1}}\,{\rm{mol/kg}}\]
The mass of water is 5.40 kg because the density is 1 g/mL, which means there are 16.1 mol of solute in one kg of water.
We need to find how many moles of solute we have in 5.40 kg of water.
\[{\rm{n}}\,{\rm{(solute)}}\,{\rm{5}}{\rm{.40}}\;\cancel{{{\rm{kg}}\;{\rm{solvent}}}}\;{\rm{ \times }}\;\frac{{{\rm{16}}{\rm{.1}}\,{\rm{mol}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}\;{\rm{solvent}}}}}}{\rm{ = }}\,86.94\,{\rm{mol}}\]
The mass of ethylene glycol would be:
\[{\rm{m}}\,{\rm{(}}{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{6}}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{86}}{\rm{.94}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{62}}{\rm{.1}}\;{\rm{g}}}}{{{\rm{1}}\,{\rm{mol}}}}\;{\rm{ = }}\,{\rm{5,399}}\,{\rm{g}}\,{\rm{ = }}\,{\rm{5}}{\rm{.40}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{3}}}\,{\rm{g}}\]
So, to prepare an antifreeze with a freezing point of -30 oC, ethylene glycol and water are mixed in a 1:1 mass ratio.
A sample of 23.0 g naphthalene (C10H8) was added to benzene (C6H6) and the resulting solution had a boiling point of 83.7 oC. How many liters of benzene were used to prepare the solution if the normal boiling point of benzene is 80.1 oC and the density is 0.877 g/mL?
0.144 L
The plan is to determine the mass of benzene from the molality and convert it to L.
ΔTb= 83.7 – 80.1 = 3.60 oC
The moles of naphthalene are calculated from the mass and the molar mass:
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{{\rm{10}}}}{{\rm{H}}_{\rm{8}}}{\rm{)}}\;{\rm{ = }}\,{\rm{23}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{128}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.1794}}\;{\rm{mol}}\]
Let’s set the mass of benzene as x kg, and write the expression for the molality:
\[m\, = \,\frac{{\Delta T}}{{{K_b}}}\;{\rm{ = }}\;\frac{{{\rm{3}}{\rm{.60}}}}{{{\rm{2}}{\rm{.53}}}}\,{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.1794}}}}{{\rm{x}}}\;{\rm{ = }}\frac{{{\rm{n}}\,{\rm{(solute)}}}}{{{\rm{kg}}\;{\rm{(solvent)}}}}\]
3.60x = 2.53 x 0.1794
3.60 x = 0.45389
x = 0.126 kg
This corresponds to 126 g, and the volume is:
\[{\rm{v}}\,{\rm{(benzene)}}\;{\rm{ = }}\,{\rm{126}}\;{\rm{g}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mL}}}}{{{\rm{0}}{\rm{.877}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{144}}\;{\rm{mL}}\;{\rm{ = }}\;{\rm{0}}{\rm{.144}}\;{\rm{L}}\,\]
You are planning a winter trip and you have an antifreeze solution that is 40.0 % by mass of ethylene glycol (C2H6O2) in water. Would this antifreeze be good enough for the trip considering that the temperature goes down as far as -30.0 °C? Ethylene glycol is a nonelectrolyte.
The antifreeze wouldn’t be suitable.
The aim here is to find the ΔTf and see if it is greater than 30.0 oC. If it is, then the antifreeze would be suitable.
ΔTf = mKf
The Kf for water is 1.86 oC/m, so we need to determine the molality.
Suppose we take 1.00 kg of water, which means there would be 0.400 kg of ethylene glycol. The moles of ethylene glycol then would be:
\[{\rm{n}}\,{\rm{(}}{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{6}}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\,{\rm{400}}{\rm{.}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{62}}{\rm{.1}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{6}}{\rm{.44}}\;{\rm{mol}}\]
The molality of the solution is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{6}}{\rm{.44}}\;{\rm{mol}}}}{{{\rm{1}}{\rm{.00}}\,{\rm{kg}}}}\; = \;6.44\,m\]
ΔTf = mKf = 6.44 m x 1.86 = 12.0 oC
The freezing point will only drop by 12.0 oC, so this ratio doesn’t yield a suitable antifreeze to drive at -30 oC.
Calculate the osmotic pressure of the solution containing 3.52 g of urea (NH2)2CO) in 485 mL of solution at 298 K.
2.95 atm
The osmotic pressure is calculated by the following formula:
ᴨ = MRT
So, we need to find the concentration of urea. The molar mass of urea is 60.1 g/mol, therefore,
\[{\rm{n}}\;{\left( {{\rm{N}}{{\rm{H}}_{\rm{2}}}} \right)_{\rm{2}}}{\rm{CO)}}\;{\rm{ = }}\;{\rm{3}}{\rm{.52}}\,{\rm{g}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{60}}{\rm{.1}}\,{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0586}}\;{\rm{mol}}\]
M (NH2)2CO) = 0.0586 ÷ 0.485 L = 0.121 mol/L
The osmotic pressure is then equal to:
\[\Pi \; = \;MRT\; = \,\frac{{{\rm{0}}{\rm{.121}}\,{\rm{mol}}}}{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.08206}}\;{\rm{L}}\;{\rm{atm}}}}{{{\rm{K}}\,{\rm{mol}}}}\;{\rm{ \times }}\;{\rm{298}}\,{\rm{K}}\,{\rm{ = }}\,2.95\,{\rm{atm}}\]
How would you prepare 1.0 L of an aqueous solution of sucrose (C12H22O11) having an osmotic pressure of 8.5 atm at 25 oC?
Dissolve 119 g of sucrose in less than 1 L of water and then top it up to 1.0 L.
The osmotic pressure is calculated by the following formula:
ᴨ = MRT
We need to find the mass of sucrose to be dissolved in enough water to make 1.0 L solution. For this, we first need the moles of sucrose which can be determined from the molarity.
\[M\; = \,\frac{\Pi }{{RT}}\; = \;\frac{{{\rm{8}}{\rm{.5}}\,{\rm{atm}}}}{{{\rm{0}}{\rm{.08206}}\,{\rm{L}}\;{\rm{atm}}}}\,\frac{{{\rm{K}}\;{\rm{mol}}}}{{{\rm{298}}\,{\rm{K}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.348}}\;{\rm{mol/L}}\]
Because the solution needs to be 1.0 L, there should also be 0.348 mol of sucrose.
The mass of sucrose is calculated from its moles and molar mass:
m (C12H22O11) = 0.348 mol x 342.3 g/mol = 119 g
So, to prepare the solution, we dissolve 119 g of sucrose in less than 1 L of water and then top it up to 1.0 L.
What is the average molecular mass of a nonelectrolyte biopolymer if dissolving 68.4 g of it in 1.25 L of water, produces a solution with an osmotic pressure of 2.4 atm at 25 oC.? Assume no volume change when the polymer is added.
556 g/mol
The osmotic pressure is calculated by the following formula:
ᴨ = MRT
We need to find the moles of the biopolymer in the 1.25 L solution, and use the given mass (0.684 g) to determine the molar mass. The moles of the polymer can be determined from the molarity.
\[M\; = \,\frac{\Pi }{{RT}}\; = \;\frac{{{\rm{2}}{\rm{.40}}\,{\rm{atm}}}}{{{\rm{0}}{\rm{.08206}}\,{\rm{L}}\;{\rm{atm}}}}\,\frac{{{\rm{K}}\;{\rm{mol}}}}{{{\rm{298}}\,{\rm{K}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0981}}\;{\rm{mol/L}}\]
This means in 1 L of solution, there is 0.0981 mol of the polymer. In 1.25 L solution, there will be:
n (polymer) = 1.25 L x 0.0981 mol/L = 0.123 mol
The molar mass of the polymer is then:
M (polymer) = 68.4 g ÷ 0.123 mol = 556 g/mol
Properties of Electrolyte Solutions
A solution is prepared by dissolving 0.248 mol of NaCl in 1.85 mol of H2O. Calculate the vapor pressure of the solution at 40 °C. The vapor pressure of pure water at 40 °C is 55.0 torr.
43.4 torr
The key part in solving problems with electrolytes is to remember that they dissociate into ions and because the colligative properties depend on the number of dissolved particles, we need to use the moles of the ions and not the salt.
For example, NaCl dissociates in two ions:
NaCl(aq) →Na+(aq) + Cl–(aq)
Therefore, the number of moles for the particles is 2 x 0.248 = 0.496 mol.
The number of ions is usually given by the van’t Hoff factor which is close to the number of ions produced upon the dissociation. So, in this case, it should be about 2. If the van’t Hoff factor is not given, we usually assume it based on the number of ions.
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
We have the vapor pressure of pure water; Po (H2O) = 55.0 Torr, so the only missing part is the mole fraction of the solvent (water in this case) which is the ratio of the moles of solvent over the total moles of the solvent and the solute:
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,2{\rm{n}}\,{\rm{(NaCl)}}}}{\rm{ }}\]
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{1}}{\rm{.85}}\,{\rm{mol}}}}{{\left( {{\rm{1}}{\rm{.85}}\;{\rm{ + }}\,{\rm{2}}\,{\rm{x 0}}{\rm{.248}}} \right)\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.78857}}\;{\rm{ }}\]
Psolution = 0.78857 x 55.0 torr = 43.4 torr
Calculate the vapor pressure of a solution prepared by dissolving 46.0 g of K2SO4 in 200. g water at 25 °C. The vapor pressure of pure water at 25 °C is 23.8 torr.
22.2 torr
The vapor pressure of the solution is calculated by the following formula:
\[{P_{solution}}\, = \;{\chi _{solvent}}{P^o}_{solvent}\]
K2SO4 is a strong electrolyte and completely dissociates in aqueous solutions:
K2SO4(aq) →2K+(aq) + SO42-(aq)
There are three ions forming from each K2SO4, so we assume the van’t Hoff factor is 3.
The moles of K2SO4 and water are:
\[{\rm{n}}\,{\rm{(}}{{\rm{K}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\,{\rm{46}}{\rm{.0}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{174}}{\rm{.3}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.264}}\;{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ = }}\,2{\rm{00}}{\rm{.}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{1}}\,{\rm{8}}{\rm{.0}}\;\cancel{{\rm{g}}}}}\; = \,11.1\;{\rm{mol}}\]
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}}{{{\rm{n}}\,{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\;{\rm{ + }}\,{\rm{3n}}\,{\rm{(}}{{\rm{K}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}}{\rm{ }}\]
\[{\chi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ = }}\;\frac{{{\rm{11}}{\rm{.1}}\,{\rm{mol}}}}{{\left( {{\rm{11}}{\rm{.1}}\;{\rm{ + }}\,{\rm{3}}\,{\rm{x 0}}{\rm{.264}}} \right)\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.933}}\;{\rm{ }}\]
Psolution = 0.933 x 23.8 torr = 22.2 torr
Calculate the freezing point of the solution prepared by dissolving 4.80 g NaCl in 25.0 g of water.
-12.2 oC
The freezing point depression is calculated by the following formula:
ΔTf = m x Kf
Kf is the freezing point depression constant for the solvent, and from the table, we find that it is 1.86 oC/m
m is the molality of the solute which is equal to:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{mol}}\;{\rm{(solute)}}}}{{{\rm{kg}}\,{\rm{(solvent)}}}}\]
The moles of particles from 4.80 g NaCl are calculated by multiplying the moles of NaCl by two since it dissociates into two ions:
\[{\rm{n}}\,({\rm{particles)}}\;{\rm{ = }}\,2\,{\rm{ \times }}\;{\rm{4}}{\rm{.80}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{58}}{\rm{.44}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.164}}\;{\rm{mol}}\]
The mass of water is 0.0250 kg, therefore, the molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.164}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.0250}}\,{\rm{kg}}}}\; = \;6.56\,m\]
The freezing point depression would then be:
ΔTf = Kfm = 1.86 oC /m x 6.56 m = 12.2 oC
The normal freezing point of water is 0oC, therefore, the freeing point of the solution will be:
0 – 12.2 = -12.2 oC
Calculate the boiling point of the solution prepared by dissolving 5.4 g FeCl3 in 36.0 g of water.
102 oC
The boiling point elevation is calculated by the following formula:
ΔTb = m x Kb
The moles of particles from 5.40 g FeCl3 are calculated by multiplying the moles of FeCl3 by four since it dissociates into four ions:
FeCl3(aq) →Fe3+(aq) + 3Cl–(aq)
\[{\rm{n}}\,({\rm{particles)}}\;{\rm{ = }}\,4\,{\rm{ \times }}\;{\rm{5}}{\rm{.40}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{162}}{\rm{.2}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.133}}\;{\rm{mol}}\]
The mass of water is 0.0360 kg, therefore, the molality of the solute is:
\[{\rm{m}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.133}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.0360}}\,{\rm{kg}}}}\; = \;3.69\,m\]
The boiling point elevation would then be:
ΔTb = Kbm = 0.512 oC /m x 3.69 m = 1.89 oC
The normal boiling point of water is 100 oC, therefore, the boiling point of the solution will be 101.89 oC ≈ 102 oC.
How many grams of NaCl were added to 1.00 L of water if the resulting solution has a freezing point of -7.40 °C? The density of water is 1.00 g/mL.
116 g
The ΔTf = 7.40 oC, and we need to use this to determine the molality of the solution. Once we know the molality, we can determine the moles of the solute, and hence the given mass.
The molality is derived from the expression of ΔTf:
ΔTf = Kfm
\[m\, = \,\frac{{\Delta T}}{{{K_f}}}\; = \;\frac{{{\rm{7}}{\rm{.40}}}}{{{\rm{1}}{\rm{.86}}}}\,{\rm{ = }}\,{\rm{3}}{\rm{.98}}\,{\rm{mol/kg}}\]
This means there are 3.98 mol of particles in 1 kg of water, and because we have 1 kg of water (1L = 1 kg), this is how many moles of particles there are in the solution.
Importantly, the number of NaCl moles is half of this because each NaCl dissociates into two ions. Therefore, we had 1.99 mol NaCl dissolved in water.
m (NaCl) = 1.99 mol x 58.44 g/mol = 116 g
Calculate the osmotic pressure of a solution prepared by dissolving 26.8 g of MgCl2 in 600. mL of water at 298 K. Assume the volume is not changing and the van’t Hoff factor for MgCl2 is 3.
34.4 atm
The osmotic pressure is calculated by the following formula:
ᴨ = MRT
So, we need to find the concentration of the particles once the MgCl2 is dissolved. The number of moles needs to be multiplied by 3 because each MgCl2 produces three ions.
\[{\rm{n}}\;{\rm{(particles)}}\;{\rm{ = }}\;{\rm{3}}\,{\rm{ \times }}\;{\rm{26}}{\rm{.8}}\,{\rm{g}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{95}}{\rm{.2}}\,{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.845}}\;{\rm{mol}}\]
The concentration of the particles is:
M (particles) = 0.845 ÷ 0.600 L = 1.41 mol/L
The osmotic pressure is then equal to:
\[\Pi \; = \;MRT\; = \,\frac{{{\rm{1}}{\rm{.41}}\,{\rm{mol}}}}{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.08206}}\;{\rm{L}}\;{\rm{atm}}}}{{{\rm{K}}\,{\rm{mol}}}}\;{\rm{ \times }}\;{\rm{298}}\,{\rm{K}}\,{\rm{ = }}\,34.4\,{\rm{atm}}\]