Another colligative property of solutions is the osmotic pressure. So, what is osmotic pressure? To understand it, let’s imagine a tube with a semipermeable membrane that separates a solvent from a solution:

 

 

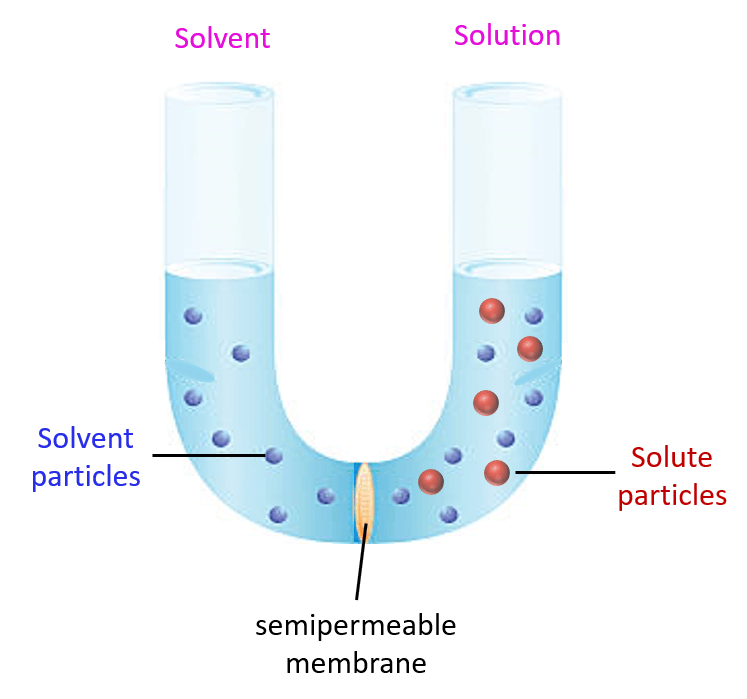
The semipermeable membrane allows passing of the solvent molecules but not the solute particles. So, the solvent molecules can pass either to the solution and dilute the concentration of the solute, or they can move from the solution to the solvent. It turns out that they move to the solution because they mix with the solute particles which increases the entropy and therefore, is the favorable direction. This movement of water, or another solvent, is called osmosis:

 

 

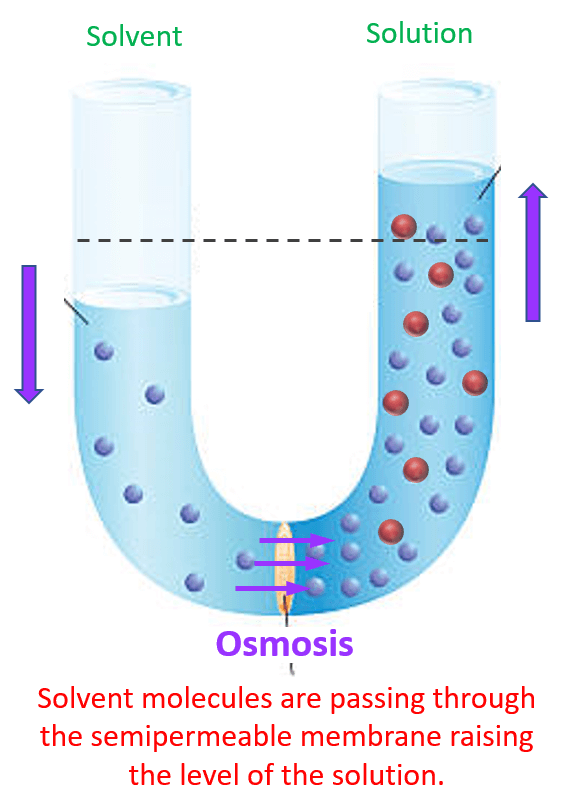
The next question is for how long does this process continue? As the osmosis continues, the solution level on the right side of the cell rises, while the water level on the left side of the cell falls. However, because of the higher level of the liquid in the solution cell, there is an excess weight which eventually stops the levels when an equilibrium is reached. That is when the amount of solvent passing in both directions is equal.

Now, what is the osmotic pressure here? Imagine if we tried to stop the osmosis when the levels were not equal by pressing on the liquid in the solution cell. This pressure, required to stop the osmosis, is called the osmotic pressure:

 

 

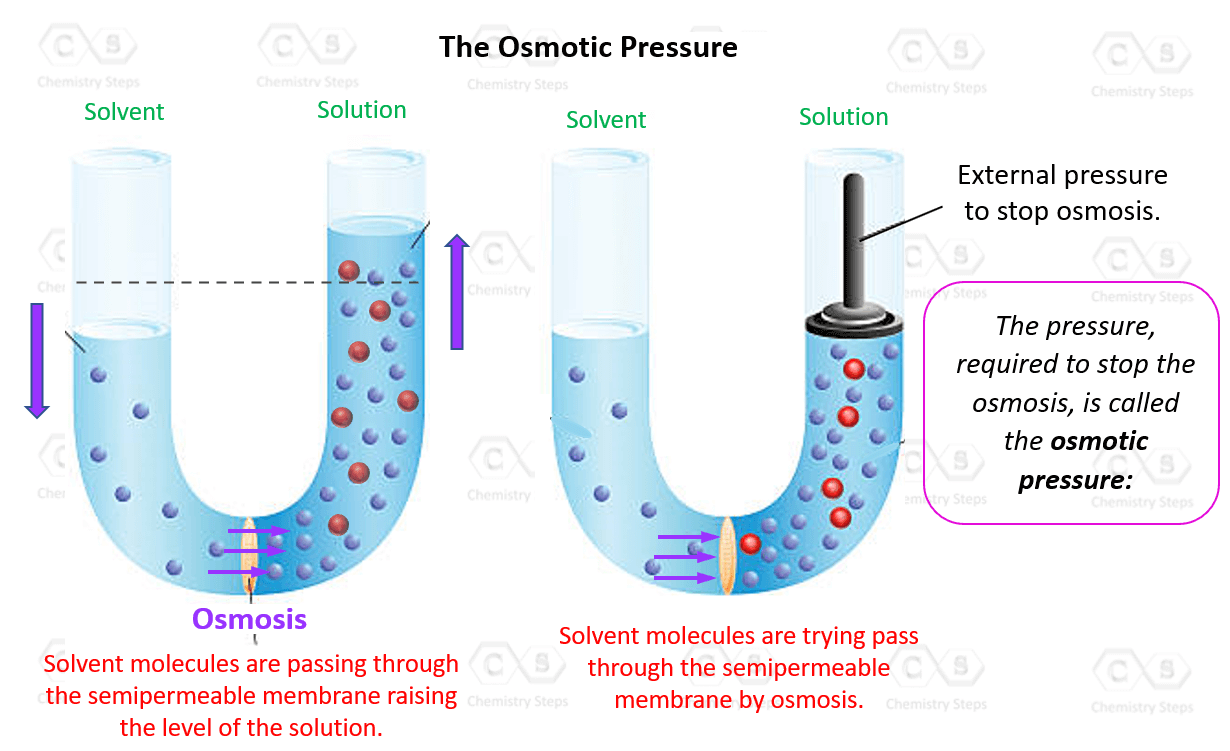
In a more general definition, we can say that osmotic pressure is the pressure required to stop the movement of solvent to a more concentrated solution.

 

Calculating the Osmotic Pressure 

The osmotic pressure is calculated by the following equation:

 

 

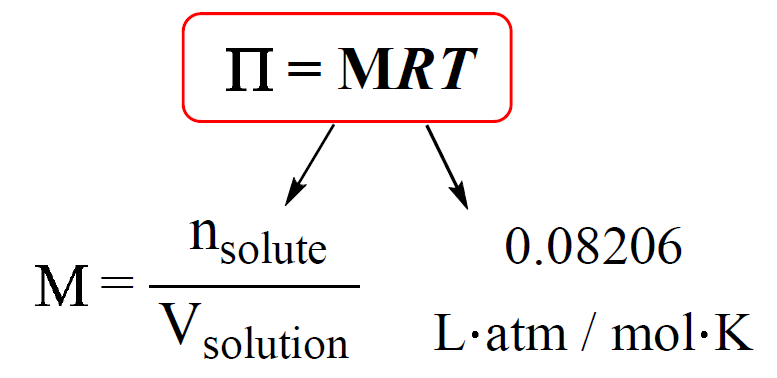
M is the molarity of the solution, T is the temperature (in Kelvin), and R is the ideal gas constant (0.08206 L · atm / mol · K).

 

For example, calculate the osmotic pressure of the solution containing 3.52 g of urea (NH₂)₂CO) in 485 mL of solution at 298 K.

The osmotic pressure is calculated by the following formula:

 

ᴨ = MRT

 

So, we need to find the concentration of urea. The molar mass of urea is 60.1 g/mol, therefore,

 

\[{\rm{n}}\;{\left( {{\rm{N}}{{\rm{H}}_{\rm{2}}}} \right)_{\rm{2}}}{\rm{CO)}}\;{\rm{ = }}\;{\rm{3}}{\rm{.52}}\,{\rm{g}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{60}}{\rm{.1}}\,{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0586}}\;{\rm{mol}}\]

 

M (NH₂)₂CO) = 0.0586 ÷ 0.485 L = 0.121 mol/L

 

The osmotic pressure is then equal to:

 

\[\Pi \; = \;MRT\; = \,\frac{{{\rm{0}}{\rm{.121}}\,{\rm{mol}}}}{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.08206}}\;{\rm{L}}\;{\rm{atm}}}}{{{\rm{K}}\,{\rm{mol}}}}\;{\rm{ \times }}\;{\rm{298}}\,{\rm{K}}\,{\rm{ = }}\,2.95\,{\rm{atm}}\]

 

The Osmotic Pressure of Electrolyte Solutions

When defining the colligative properties, we said that they only depend on the number of solute particles. Now, let’s say we dissolve 1 mole of NaCl in water and need to measure the osmotic pressure of the solution. The question is how many particles do we have in the solution?

Remember, NaCl is a strong electrolyte and dissociates into ions in aqueous solutions.

 

NaCl(aq)  →  Na⁺(aq) + Cl^–(aq)

 

Therefore, the concentration of the solute particles is given by the Na⁺ and Cl^– ions rather than the salt. So, if we need to calculate the molarity, we need to multiply the moles of NaCl by two.

 

For example, calculate the osmotic pressure of a solution prepared by dissolving 26.8 g of MgCl₂ in 600. mL of water at 298 K. Assume the volume is not changing and the van’t Hoff factor for MgCl₂ is 3.

The osmotic pressure is calculated by the following formula:

 

ᴨ = MRT

 

So, we need to find the concentration of the particles once the MgCl₂ is dissolved. The number of moles needs to be multiplied by 3 because each MgCl₂ produces three ions.

 

\[{\rm{n}}\;{\rm{(particles)}}\;{\rm{ = }}\;{\rm{3}}\,{\rm{ \times }}\;{\rm{26}}{\rm{.8}}\,{\rm{g}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{95}}{\rm{.2}}\,{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.845}}\;{\rm{mol}}\]

 

The concentration of the particles is:

 

M (particles) = 0.845 ÷ 0.600 L = 1.41 mol/L

 

The osmotic pressure is then equal to:

 

\[\Pi \; = \;MRT\; = \,\frac{{{\rm{1}}{\rm{.41}}\,{\rm{mol}}}}{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.08206}}\;{\rm{L}}\;{\rm{atm}}}}{{{\rm{K}}\,{\rm{mol}}}}\;{\rm{ \times }}\;{\rm{298}}\,{\rm{K}}\,{\rm{ = }}\,34.4\,{\rm{atm}}\]

 

In general, we can calculate the number of ions based on the formula of the salt. For example, 1 mole of MgBr₂ is expected to produce 3 moles of ions because each formula unit contains one Mg²⁺ and 2 Br^– ions. However, the dissociation of most ionic compounds does not occur at 100%,  and the solution of an ionic compound usually contains fewer particles than its formula suggests. The actual extent of dissociation can be expressed as a van’t Hoff factor (i).

 

 

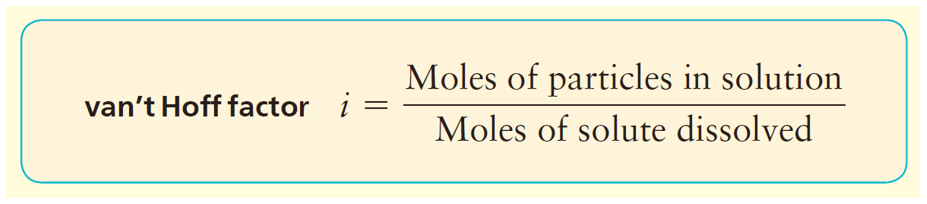
For most ionic compounds, the van’t Hoff’s constant is determined experimentally, and will likely be given to you in the test. If it is not, and there is nothing mentioned about it, you can go based on the formula of the compound. For nonelectrolytes, it is assumed to be 1 as we do not worry about their negligible dissociation.

More practice problems on the colligative properties can be found here.

 

 

Check Also

• Colligative Properties
• Vapor Pressure Lowering
• Boiling Point Elevation
• Freezing Point Depression
• Molarity, Molality, and Other Concentrations – Practice Problems
• Colligative Properties Practice Problems