In the previous two posts, we talked about the Gibbs free energy and calculating its value using either of these two equations:
ΔG°rxn = ΣnpΔGof (products) – ΣnrΔGof (reactants) (1)
ΔG°rxn = ΔH° – TΔS° (2)
There are two main scenarios that restrict the use of these equations: The first one is that strictly speaking, the Gibbs free energy should only be used for reactions carried out at 25 oC since ΔHof and ΔSo are given for that temperature.
This pertains to the first equation more as the Gibbs free energy is more sensitive to temperature and the values of standard free energies of formations vary significantly when measured at different temperatures. Therefore, we cannot use the tabulated values of ΔG°f to calculate the ΔG°rxn for a reaction carried out at higher temperatures.
On contrary, although the enthalpies and entropies are affected by temperature, the difference between their values is very little compared to the temperature change. As a result, the values of ΔH° and ΔS° do not change much with temperature and we can use the ΔG° = ΔH° – TΔS° equation for reactions at higher temperatures.
We will discuss these differences with an example of working with ΔG° at different temperatures in a separate post. So, now, let’s discuss the second restriction of using the equations for ΔG°.
The second restriction is that remember we mentioned that they are used for reactions where the products and reactants are in their standard conditions. Remember, standard states are defined as follows.
- Gases: It is the pure gas at a pressure of exactly 1 atm.
- Liquids and Solids: It is the pure substance in its most stable form at a pressure of 1 atm and at the temperature of interest (usually at 25 oC).
- A Substance in Solution: It is when the concentration is exactly 1 M.
Do not confuse these with STP – standard temperature and pressure for gases defined as 273.15 K (0 °C, 32 °F) and an absolute pressure of exactly 105 Pa (100 kPa, 1 bar).
The problem is that very often the reaction components are not in their standard conditions. Moreover, their concentrations is changing in the course of the reaction. So, how do we calculate the Gibbs free energy change for reaction as nonstandard-state conditions?
The reaction quotient from the equilibrium chapter is what comes to the rescue.
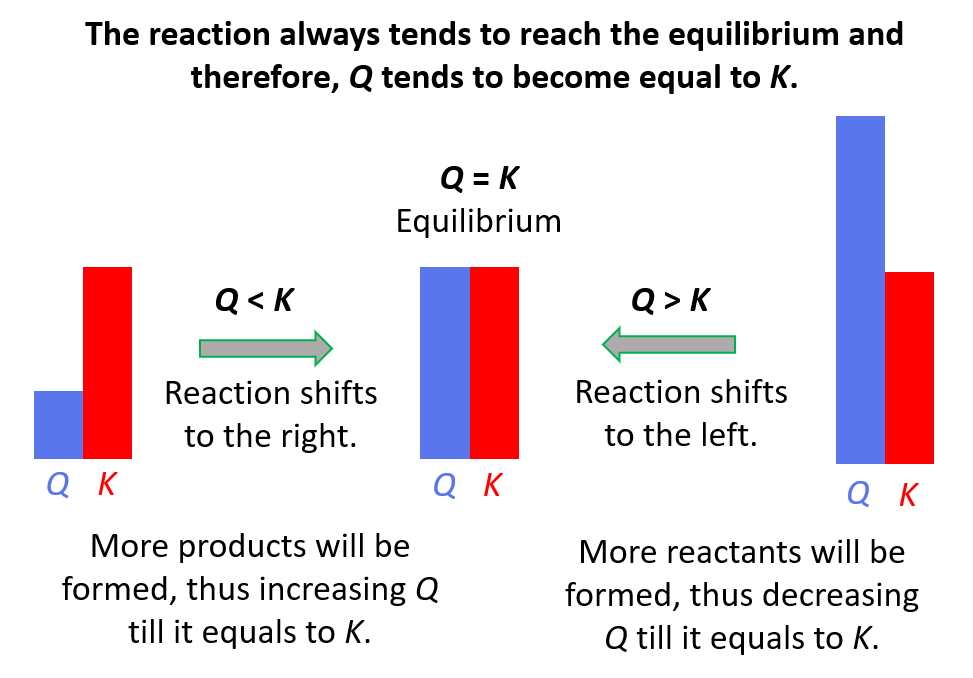
Remember, if
- Q < K Reaction tends to form more products.
- Q > K Reaction tends to form more reactants.
- Q = K Reaction is already at equilibrium.
Now the reaction quotient and the Gibbs free energy for standard-state conditions are combined into an equation that allows calculating the ΔGrxn for nonstandard-state conditions:
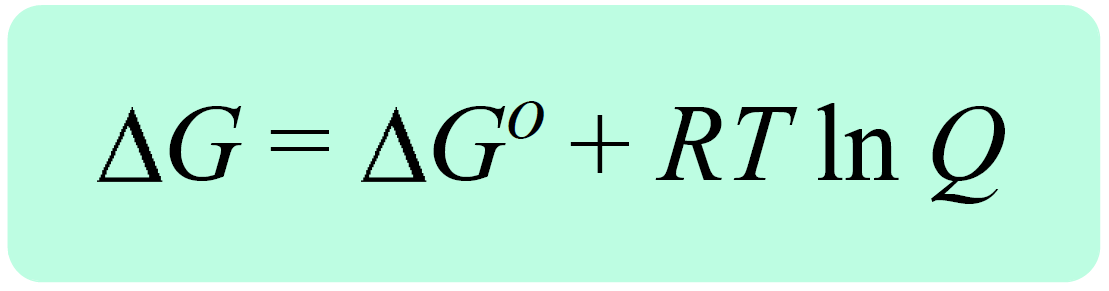
where ΔG is the free-energy change under nonstandard-state conditions, ΔG° is the free-energy change under standard-state conditions, R is the gas constant, T is the temperature in kelvin, and Q is the reaction quotient
For reactions that involve both gases and solutes in solution, the reaction quotient Q contains partial pressures of gases in atmospheres and molar concentrations of solutes. For example,
2H+(aq) + Zn(s) ⇆ H2(g) + Zn2+(aq)
\[K/Q\, = \,\frac{{{\rm{[Z}}{{\rm{n}}^{{\rm{2 + }}}}{\rm{]}}{P^2}_{{{\rm{H}}_{\rm{2}}}}}}{{{{[{{\rm{H}}^{\rm{ + }}}]}^2}}}\]
So, how do we understand the correlation between the Q, ΔGorxn, and the ΔGrxn?
There are three possibilities for the value of the Q which tell us about the spontaneity of the reaction:
1) Q = 1: The reaction quotient is equal to one. This corresponds to the standard-state conditions, and, in this case, RT ln Q becomes zero which indicates that ΔG = ΔGo.
2) Q < 1: The reaction mixture contains mainly reactants making Q smaller than one, Q < 1. The logarithm term becomes negative (RT ln Q < 0), and therefore, ΔG < ΔGo which indicates that the reaction under these conditions tends to be more spontaneous than at standard-state conditions. It may not necessarily be spontaneous because whether the ΔG is negative or not will depend on the value of ΔGo.
Only if the ratio of the reactants and products is extremely high will guarantee that the reaction is spontaneous because in this case, Q is almost equal to zero which makes the term RT ln Q a very large negative number.
3) Q > 1: If the reaction mixture contains mainly products, Q becomes much greater than 1 making the term RT ln Q a large positive number as well. This will mean the reaction is most likely nonspontaneous unless ΔGo is an extremely negative number.
On the other hand, this also indicates that the reverse reaction is spontaneous.
For example, using the data from an appendix of thermodynamic data in your textbook, calculate ΔG for the reaction at 298 K and the following partial pressures. Is the reaction spontaneous?
4HCl(g) + O2(g) ⇆ 2Cl2(g) + 2H2O(g)
PHCl = 50.0 mmHg, PO2 = 35.0 mmHg, P H2O = 125 mmHg, PCl2 = 182 mmHg
Solution: The reaction is under nonstandard conditions, therefore, we need to use the following equation:
ΔG = ΔG° + RT ln Q
Where Q is the reaction quotient, and in this case, it is:
\[{Q_p} = \frac{{{P^{\rm{2}}}_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}{P^2}_{{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}{{{P^4}_{{\rm{HCl}}}{P_{{{\rm{O}}_{\rm{2}}}}}}}\]
Convert the units of pressure to atm. 1 atm = 760 mmHg, therefore,
\[P\,\left( {{\rm{HCl}}} \right)\,{\rm{ = }}\;{\rm{50}}{\rm{.0}}\,\cancel{{{\rm{mmHg}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{atm}}}}{{{\rm{760}}\,\cancel{{{\rm{mmHg}}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.06579}}\,{\rm{atm}}\]
\[P\,\left( {{{\rm{O}}_{\rm{2}}}} \right)\,{\rm{ = }}\;{\rm{35}}{\rm{.0}}\,\cancel{{{\rm{mmHg}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{atm}}}}{{{\rm{760}}\,\cancel{{{\rm{mmHg}}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.04605}}\,{\rm{atm}}\]
\[P\,\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\,{\rm{ = }}\;{\rm{125}}\,\cancel{{{\rm{mmHg}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{atm}}}}{{{\rm{760}}\,\cancel{{{\rm{mmHg}}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.1645}}\,{\rm{atm}}\]
\[P\,\left( {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right)\,{\rm{ = }}\;{\rm{182}}\,\cancel{{{\rm{mmHg}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{atm}}}}{{{\rm{760}}\,\cancel{{{\rm{mmHg}}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.2395}}\,{\rm{atm}}\]
\[{Q_p} = \frac{{{P^{\rm{2}}}_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}{P^2}_{{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}{{{P^4}_{{\rm{HCl}}}{P_{{{\rm{O}}_{\rm{2}}}}}}}\; = \;\frac{{{{\left( {0.1645} \right)}^2}{{\left( {0.2395} \right)}^2}}}{{{{\left( {0.06579} \right)}^4}\left( {0.04605} \right)}}\; = \;1790.6\]
Next, we need to determine the ΔG°, and again, because the reaction is carried out at 25 oC, we can use the ΔG°f from the appendix.
4HCl(g) + O2(g) ⇆ 2Cl2(g) + 2H2O(g)
ΔG° = [2 ΔGof (Cl2(g)) + 2 ΔGof (H2O(g))] – [4 ΔGof (HCl(g)) + ΔGof (O2(g))]
ΔG° = [2 x 0 + 2 x (-229)] – [4 x (-95) + 0] = -78 kJ
And now, we can use enter the numbers in the equation for ΔG at nonstandard conditions:
\[\Delta G\, = \, – 78\, \times \,{10^3}\,{\rm{J}}\,{\rm{ + }}\,{\rm{8}}{\rm{.314}}\frac{{\rm{J}}}{{\cancel{{\rm{K}}}{\rm{ \times mol}}}}\,{\rm{298}}\,\cancel{{\rm{K}}}\,{\rm{ln}}\,{\rm{1790}}{\rm{.6 = }}\,{\rm{ – 5}}{\rm{.94}}\, \times \,{\rm{1}}{{\rm{0}}^{\rm{4}}}\,{\rm{J}}\;{\rm{ = }}\; – 59.4\,{\rm{kJ}}\,\]
Although ΔG is less negative than ΔG° because Qp is larger than 1 and ln Qp is positive, the reaction is still spontaneous because ΔG° has a very negative value.
In the next article, we will discuss the relationship between Gibbs free energy and equilibrium constant.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Gibbs Free Energy
- The Effect of 𝚫H, 𝚫S, and T on 𝚫G – Spontaneity
- Entropy and State Change
- Entropy Changes in the Surroundings
- 𝚫Gorxn from the Free Energies of Formation
- Gibbs Free Energy and Hess’s Law
- Gibbs Free Energy and Equilibrium Constant
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
