Recall how we used the Hess’s law to calculate the enthalpy change (ΔH) for a reaction without having the enthalpies of formation for any or some of the components in the reaction.
On the basis of the Hess’s law is the fact that enthalpy is a state function, and therefore, it does not matter what route the conversion the molecules take, but rather what the enthalpies of the reactants and products are.
Remember, a state function is a variable that only depends on the initial and final states and now how it was achieved. For example, altitude is a state function and wouldn’t matter how two hikers meet at a 500 ft altitude. One may be on his way to the top, and the other going back having behind a longer walk distance:
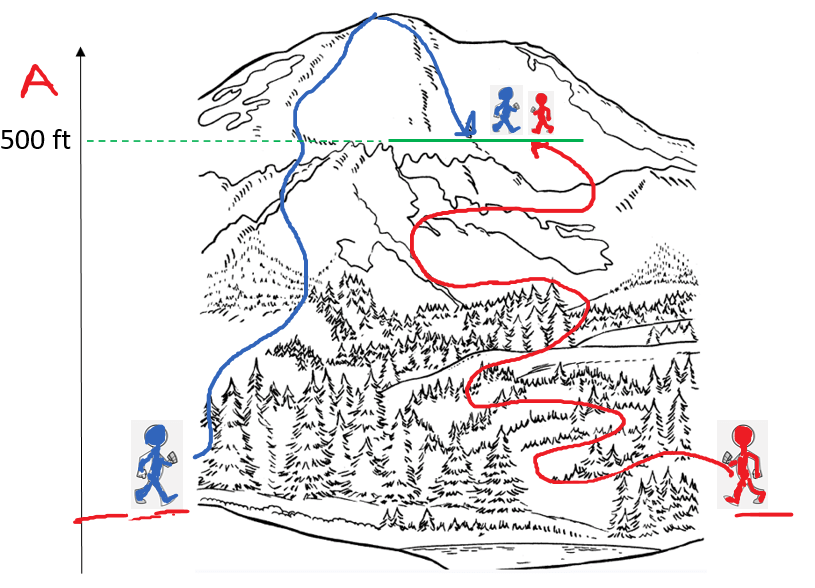
Compare this to the enthalpy change for the following stepwise reaction converting molecules A and B to molecule C:
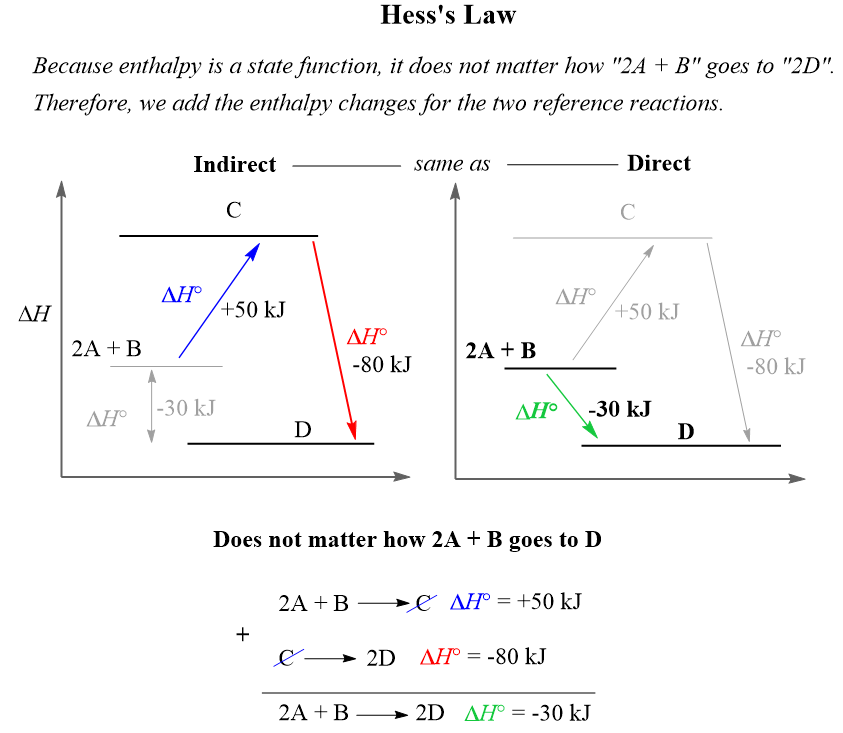
The enthalpy change is the same if molecules A and B are converted to C, and then D compared to if they go directly to D. Therefore, if we add the values of the enthalpies with their signs, the final result will be the enthalpy change of the net conversion.
Now, because Gibss free energy is also a state function, we can apply the same strategy and calculate the ΔGo for a stepwise reaction from the sum of the changes in ΔGo for each step.
For example, given the data for the three combustion reactions below, calculate the free energy of the reaction producing methanol (CH3OH) from carbon monoxide and hydrogen gas.
CO(g) + 2H2(g) → CH3OH(g), ΔGo = ?
1) 2CO(g) + O2(g) → 2CO2(g), ΔGo= -514 kJ
2) 2H2(g) + O2(g) → 2H2O(g), ΔGo = -458 kJ
3) 2CH3OH(g) + 3O2(g) → 2CO2(g) + 4H2O(g), ΔGo = −1378 kJ
Solution: The first two equations seem to be in the correct directions since they contain CO and H2 as reactants which is what we have in the target equation.
The third equation, however, must be reversed because the methanol here is a reactant while in the target equation, it is a product. So, let’s reverse it and label as 3a:
3a) 2CO2(g) + 4H2O(g) → 2CH3OH(g) + 3O2(g), ΔGo = +1378 kJ
Let’s add equations 1, 2, and 3a and see what we get:
1) 2CO(g) + O2(g) → 2CO2(g), ΔGo = -514 kJ
+
2) 2H2(g) + O2(g) → 2H2O(g), ΔGo = -458 kJ
+
3a) 2CO2(g) + 4H2O(g) → 2CH3OH(g) + 3O2(g), ΔGo = +1378 kJ
You may notice that there are four moles of water on the left side (equation 3a), but only two moles on the right side (equation 2). This means we need to multiply equation two with its ΔG value by two. Let’s do that and label the new equation as 2a:
2a) 4H2(g) + 2O2(g) → 4H2O(g), ΔGo = -916 kJ
And now, we can add equations 1, 2a, and 3a:
1) 2CO(g) + O2(g) → 2CO2(g), ΔGo = -514 kJ
+
2a) 4H2(g) + 2O2(g) → 4H2O(g), ΔGo = -916 kJ
+
3a) 2CO2(g) + 4H2O(g) → 2CH3OH(g) + 3O2(g), ΔGo = +1378 kJ
2CO(g) + O2(g) + 4H2(g) + 2O2(g) + 2CO2(g) + 4H2O(g) → 2CO2(g) + 4H2O(g) + 2CH3OH(g) + 3O2(g)
Cancel the same molecules on both sides of the equation:
2CO(g) + O2(g) + 4H2(g) + 2O2(g) + 2CO2(g) + 4H2O(g) → 2CO2(g) + 4H2O(g) + 2CH3OH(g) + 3O2(g)
ΔGo = -514 kJ + (-916 kJ) + 1378 kJ/mol = -52 kJ
2CO(g) + 4H2(g) → 2CH3OH(g), ΔGo = -52 kJ
The last step is to divide the equation by two to match the target reaction:
CO(g) + 2H2(g) → CH3OH(g), ΔGo = -26 kJ
These types of problems are no different than what we did when discussing Hess’s law. Check the article and practice examples at the links.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Gibbs Free Energy
- The Effect of 𝚫H, 𝚫S, and T on 𝚫G – Spontaneity
- Entropy and State Change
- Entropy Changes in the Surroundings
- 𝚫Gorxn from the Free Energies of Formation
- Gibbs Free Energy Under Nonstandard Conditions
- Gibbs Free Energy and Equilibrium Constant
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
