In the previous post, we discussed the correlation between the entropy change of the surroundings, ΔSsurr, and the enthalpy change of the system.
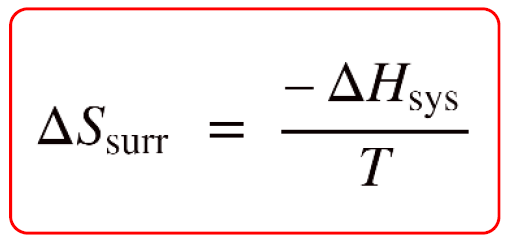
This relationship is useful for determining whether a given reaction is spontaneous or not because it allows calculating the ΔSuniv if the ΔSsys is known or can be determined.
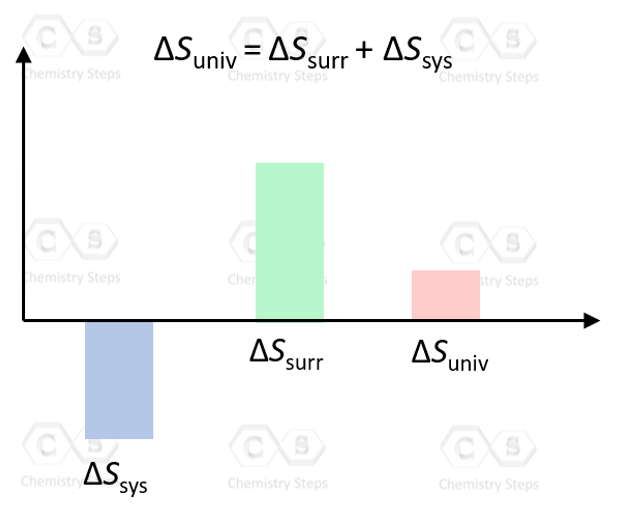
Remember, according to the second law of thermodynamics, the process is spontaneous only if the entropy of the universe is increasing, ΔSuniv > 0:
Now, it is not very practical to deal with the entropy of the surroundings and calculate the entropy change of the universe every time we need to determine whether a reaction is spontaneous or not. In chemistry, our focus is usually on the reaction, which is the system, so it would be more convenient to work with the parameters of the system without worrying about the surroundings.
And this is where the famous Gibbs free (G) energy comes into play as it combines the system’s enthalpy and entropy:
G = H − TS
The Gibbs free energy change (ΔG) is what is used for determining if the process is spontaneous or not.
To derive the expression for the Gibbs free energy, we combine the following two equations that we have already discussed:
\[\Delta {S_{surr}}\, = \;\frac{{ – \Delta {H_{sys}}}}{T}\]
ΔSuniv = ΔSsurr + ΔSsys
Plugging this expression in the equation for ΔSsurr, and multiplying everything by –T, we get:
\[ – T\Delta {S_{univ}}\, = \;\frac{{ – \cancel{T}\; \times \;( – \Delta {H_{sys}})}}{{\cancel{T}}}\; – \;T\Delta {S_{sys}}\; = \, – T\Delta {S_{univ}}\; = \;\Delta {H_{sys}}\, – \;T\Delta {S_{sys}}\]
The term, (-TΔSuniv) is the Gibbs free energy change (ΔGo), and it is a comprehensive quantity to assess the spontaneity of a process because it takes into account the enthalpy, entropy, and temperature.
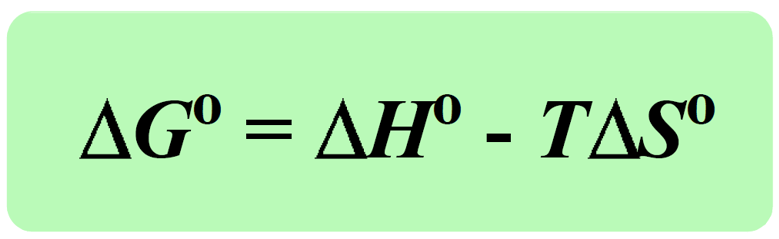
Notice that all the terms on the right are related to the system and therefore, to calculate the ΔGo we only need to have data pertaining to the system.
Just like for the enthalpy and entropy the superscript indicates standard-state conditions.
ΔG and Spontaneity of Reaction
So, ΔGo is calculated by the parameters of the system, but it silently includes the ΔSuniv just with the opposite sign. Therefore, because a spontaneous process is associated with a positive ΔSuniv, negative ΔG (exergonic) indicates a spontaneous, while positive ΔG (endergonic) means a nonspontaneous process. When G = 0, the system is at equilibrium.
Another way to look at this is that G is energy and remember, any process tends to go downhill energetically because lower energy means more stability.
To summarize, remember that:
♦ ΔG is proportional to the negative of ΔSuniv.
♦ ΔG < 0: A negative ΔG corresponds to a spontaneous process.
♦ ΔG > 0: A positive ΔG corresponds to a nonspontaneous process.
♦ ΔG = 0: The system is at equilibrium. There is no net change.
Example: Given the values of ΔH and ΔS, which of the following changes will be spontaneous at constant T and P?
a) ΔH = +35 kJ, ΔS = +10 J/K, T = 300. K
b) ΔH = +45 kJ, ΔS = +153 J/K, T = 312 K
Solution
a) Make sure the units of ΔH and ΔS match in terms of Joules.
ΔH = +35 kJ = 35 x 103 J
ΔG = 35 x 103 J – 300. K ΔS x 15.0 J/K = 30,500 J
ΔG > 0, therefore, the process is nonspontaneous.
b) Again convert the units to match the Joules.
ΔH = +45 kJ = 45 x 103 J
ΔG = 45 x 103 J – 312 K x 153 J/K = -2736 J
ΔG < 0, therefore, the process is spontaneous.
In the next article, we will discuss the correlation between the ΔG, ΔH, and ΔS and the spontaneity of the reaction depending on the sign of these quantities.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Effect of 𝚫H, 𝚫S, and T on 𝚫G – Spontaneity
- Entropy and State Change
- Entropy Changes in the Surroundings
- 𝚫Gorxn from the Free Energies of Formation
- Gibbs Free Energy and Hess’s Law
- Gibbs Free Energy Under Nonstandard Conditions
- Gibbs Free Energy and Equilibrium Constant
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
