When calculating the enthalpy or any other thermodynamic parameter, we are usually focused on the system. For example, we may use a calorimeter to calculate the enthalpy of a reaction which is the point of our interest, and therefore, it is the system.
Now, there are instances when we need to determine the entropy change of the surroundings, ΔSsurr and because the surroundings are the rest of the universe, it raises the question of how it is even possible.
It turns out, this is not so complicated because the entropy of the surroundings is proportional to the enthalpy change of the system, ΔHsys with a reverse sign:
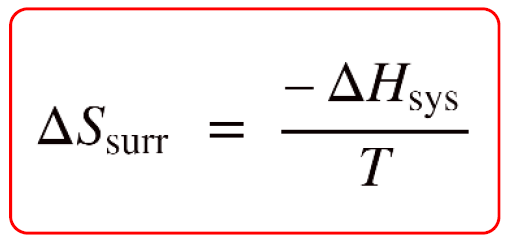
So, why are they proportional and why the minus sign? To understand this, let’s consider an exothermic reaction. The enthalpy of the system decreases because it gives off heat to the surroundings. Importantly, this heat increases the kinetic energy of the molecules in the surroundings which in turn increases their entropy because they go into a more random state with a higher degree of freedom.
On the other hand, an endothermic reaction absorbs the heat from the surroundings, i.e. from the molecules of the surroundings which decreases their entropy.
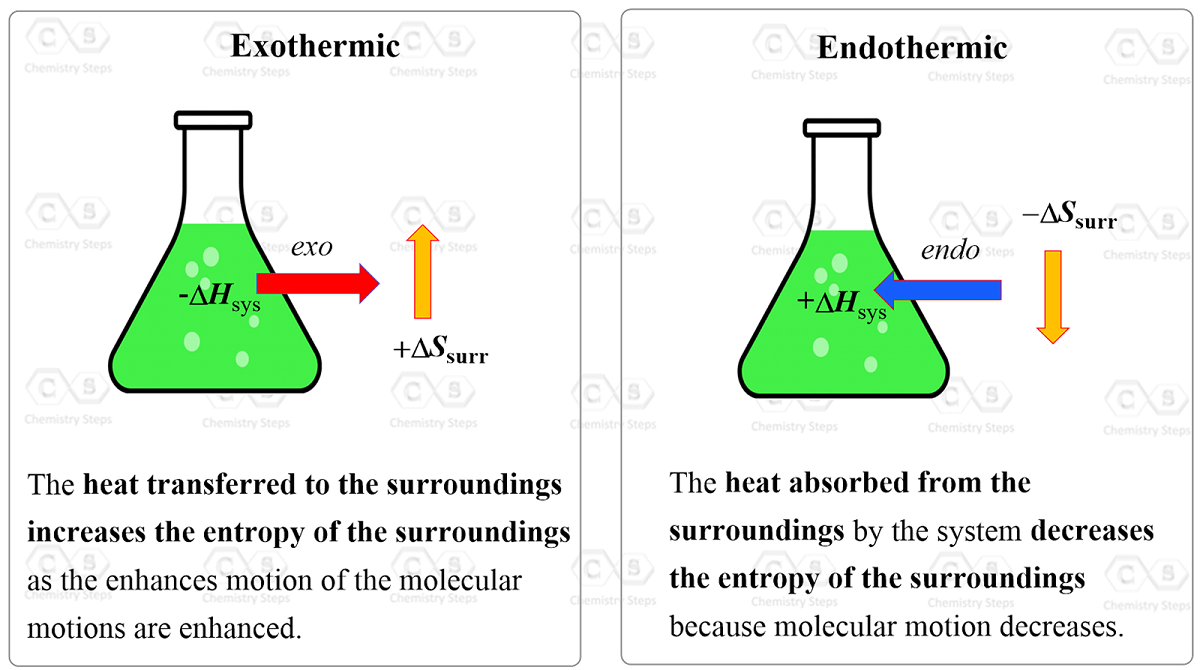
In simple words, this shows that entropy is proportional to heat and wherever the heat goes, the entropy of that region increases with it. Therefore, whatever gives off heat, loses some entropy.
Calculating the ΔSsurr
Example: Calculate the ΔSsurr for a certain reaction with ΔH°rxn = -2560 kJ at carried out at 298 K
Solution: Since entropy is usually given in J/K mol, we first convert the units of ΔH°rxn:
ΔH°rxn = -2560 kJ = -2.56 x 106 J/mol
\[\Delta {S_{{\rm{surr}}}}\; = \,\frac{{ – \Delta {H_{{\rm{sys}}}}}}{T}\, = \;\frac{{ – \left( { – 2.56\; \times \;{{10}^6}\;{\rm{J}}} \right)}}{{298\,K}}\; = \,8.59\, \times \;{10^3}\,{\rm{J/K}}\]
The Correlation of ΔS, ΔSsys, and ΔSsurr
The correlation between the heat and entropy explains for example, why entropically unfavorable combustion of propane is a spontaneous reaction:
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(l), ΔSorxn = -374 J/K
Notice that there are more gaseous molecules on the reactants than on the products’ side, therefore, the entropy change of the reaction, ΔSorxn < 0. Notice also that the reaction is very exothermic, and the great amount of heat released from the system is consumed by the surroundings increasing its entropy. Therefore, ΔSsurr > 0.
Remember, according to the second law of thermodynamics, the process is spontaneous only if the entropy of the universe is increasing, ΔSuniv > 0:
ΔSuniv = ΔSsys + ΔSsurr > 0
As long as the ΔSsurr is large enough, it does not matter that ΔSsys is negative.
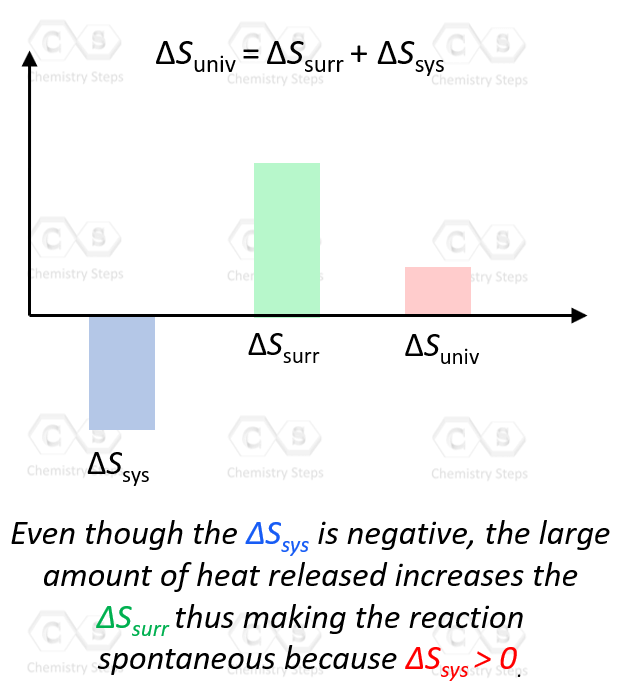
In general, if both the ΔSsys and ΔSsurr are positive, then ΔSuniv > 0 and the process is spontaneous. If one of them is negative, it does not matter whether the ΔSsys or ΔSsurr is the positive contributor to making the process spontaneous, as long as their sum is positive.
Calculating the ΔSuniv
Example: Determine whether the following reaction is spontaneous or not by calculating the ΔSuniv based on the values of ΔH °rxn, ΔS °rxn, and T. Assume that all the components in the reaction are in their standard states.
ΔH °rxn = +126 kJ; ΔS °rxn = -231 J/K; T = 298 K
Solution: The reaction is spontaneous when ΔSuniv > 0.
ΔSuniv = ΔS °rxn + ΔSsurr
We have the ΔS °rxn, and the ΔSsurr is calculated by the following formula:
\[\Delta {S_{{\rm{surr}}}}\; = \,\frac{{ – \Delta {H_{{\rm{sys}}}}}}{T}\,\]
\[\Delta {S_{{\rm{surr}}}}\; = \,\frac{{ – \Delta {H_{{\rm{sys}}}}}}{T}\, = \;\frac{{\left( { – 126\;{\rm{kJ}}} \right)}}{{298\;K}}\; = \, – {\rm{0}}{\rm{.423}}\,{\rm{kJ/K}}\;{\rm{ = }}\, – {\rm{423}}\,{\rm{J/K}}\]
ΔSuniv = ΔS °rxn + ΔSsurr = -231 J/K + -(423 J/K) = -654 J/K
ΔSuniv < 0, therefore, the reaction is not spontaneous.
The next question you may be wondering is do we have to deal with the entropy of the surroundings and calculate the entropy change of the universe every time we need to determine whether a reaction is spontaneous or not. And the answer is no, the effect of the entropy changes in the system and the universe are combined in the Gibbs free energy which is what we will talk about in the next article.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Gibbs Free Energy
- The Effect of 𝚫H, 𝚫S, and T on 𝚫G – Spontaneity
- Entropy and State Change
- 𝚫Gorxn from the Free Energies of Formation
- Gibbs Free Energy and Hess’s Law
- Gibbs Free Energy Under Nonstandard Conditions
- Gibbs Free Energy and Equilibrium Constant
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
