In the previous post, we talked about the Gibbs free energy for reactions at nonstandard-state conditions, ΔG. It is related to the free energy change of the reaction at standard-state conditions, ΔGo, and the reaction quotient, Q with the following equation:
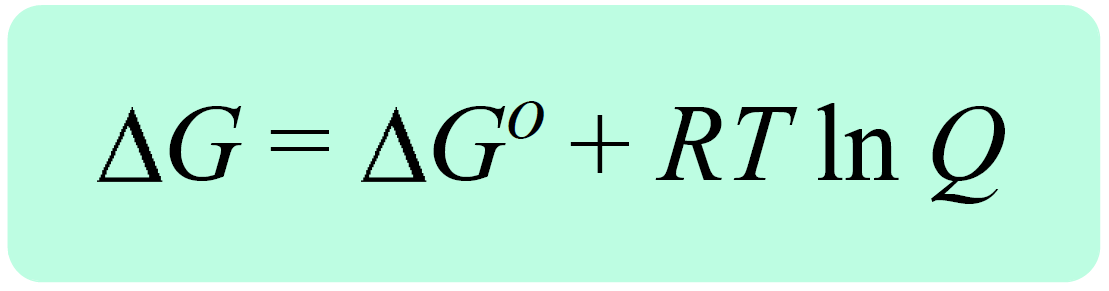
Remember, the reaction quotient is used to predict the direction of the equilibrium depending on the initial quantities of the reactants and products:
- Q < K Reaction tends to form more products.
- Q > K Reaction tends to form more reactants.
- Q = K Reaction is already at equilibrium.
Because the system always tries to reach an equilibrium, Q tends to become equal to K, and when that happens, an equilibrium is established, K = Q.
Now, by definition, when the equilibrium is established, the free energy of the reaction becomes a zero, ΔG = 0. So, if we replace Q with K, and ΔG with 0, we obtain a very important equation in chemistry that correlates the equilibrium constant the ΔGo:
0 = ΔG° + RT ln K, therefore,
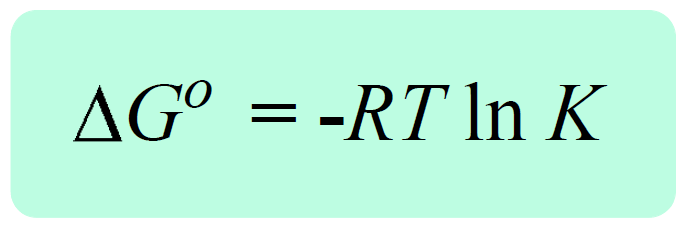
We can apply this equation to reactions in solutions, Kc and the ones involving gases in which case, KP is used. The equation can also be used for the solubility constant, Ksp.
How do we interpret this equation?
The key link here is the negative sign which tells us the larger the K, the more negative ΔG° is. Remember, a larger K indicates that the products are favored which is essentially to say that the reaction is spontaneous – it tends to proceed forward producing more products. A smaller equilibrium constant, on the other hand, makes the ΔG° larger and if it becomes a positive value, the reaction is not spontaneous anymore. This happens when K < 1, because the RT ln K term becomes negative, and the minus sign makes the ΔG° positive. Again, K < 1 means that the equilibrium mixture is mainly reactants, and therefore, the forward reaction is nonspontaneous.
To summarize the correlation between the equilibrium constant the ΔG°, we can write that:
♦ When K < 1, ln K is negative and ΔGorxn > 0. The reaction is not spontaneous.
♦ When K > 1, ln K is negative, and ΔGorxn < 0. The reaction is spontaneous.
♦ When K = 1, ln K = 0, ΔGorxn = 0. The reaction is at equilibrium.
The significance of the equation ΔG° = -RT ln K is evident when, for example, the equilibrium constant of the reaction cannot be determined experimentally. What we do then is calculate the ΔG° and use it to determine the equilibrium constant.
For example, using the data from an appendix for thermodynamic data, calculate the equilibrium constants of the following reaction at 25 °C:
NO(g) + O3(g) ⇆ NO2(g) + O2(g)
Solution: The first is to determine the ΔGo from the standard free energies of formation using the following equation:
ΔG°rxn = ΣnpΔGof (products) – ΣnrΔGof (reactants)
NO(g) + O3(g) ⇆ NO2(g) + O2(g)
ΔG° = [ΔGof (NO2(g)) + ΔGof (O2(g))] – [ΔGof (NO(g)) + ΔGof (O3(g))]
ΔG° = [(52 + 0) – (87 + 163)] = -198 kJ
ΔG° = –RT ln K
\[\ln \,K\; = \;\frac{{ – \Delta G^\circ }}{{RT}}\]
Taking antilog to get an expression for K:
\[K\; = \;{e^{\frac{{ – \Delta G^\circ }}{{RT}}}}\]
You can either calculate the exponent term separately or use the numbers in this equation.
\[K\; = \;{e^{\frac{{{\rm{ – }}\left( {{\rm{ – 198}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{3}}}\,{\rm{J}}} \right)}}{{{\rm{8}}{\rm{.314}}\,{\rm{J/K}} \cdot {\rm{mol}}\, \cdot {\rm{298}}\;{\rm{K}}}}}}\, = \,{e^{79.9}}\; = \;5.01\, \times \,{10^{34}}\,\]
The equilibrium constant is very large, and this is in agreement with a highly negative ΔG°.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Gibbs Free Energy
- The Effect of 𝚫H, 𝚫S, and T on 𝚫G – Spontaneity
- Entropy and State Change
- Entropy Changes in the Surroundings
- 𝚫Gorxn from the Free Energies of Formation
- Gibbs Free Energy and Hess’s Law
- Gibbs Free Energy Under Nonstandard Conditions
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
