Very often, solutions are stored in concentrated forms called stock solutions. Now, if a solution with a lower concentration is needed, some of the stock solution is mixed with a solvent and a dilute solution is obtained.
Concentrated solution + Solvent → Dilute solution
This process is called dilution and it is very convenient because the concentration of the dilute solution can be easily calculated using the dilution formula:
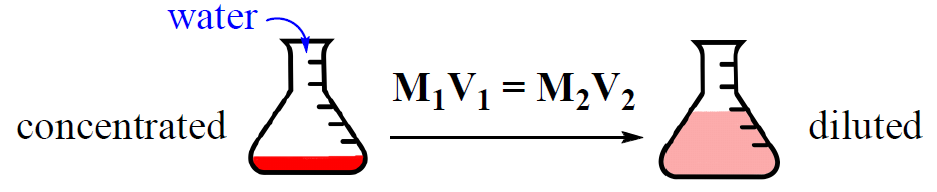
M1 and V1 are the concentration and the volume of the stock solution, and M2, V2 are the concentration and the volume of the final solution that we prepare.
For example, how many liters of 0.350 molar sodium hydroxide solution can be prepared from 400.0 mL of 3.60 M solution?
First, write the given data, and for this, we need to correctly assign the M1, V1, M2, and V2.
0.350 molar solution needs to be prepared, and therefore, it is the M2 – the concentration of the final solution.
400.0 mL is the volume of the stock solution, so we assign it as V1
3.60 M is the concentration of the stock solution, so that is M1, and therefore, V2 is what we need to find.
List, this together and set up the dilution formula:
M1 = 3.60 M
V1 = 400.0 mL
M2 = 0.350 M
_________________
V2 = ?
M1V1 = M2V2
\[{{\rm{V}}_{\rm{2}}}\;{\rm{ = }}\;\frac{{{{\rm{M}}_{\rm{1}}}{{\rm{V}}_{\rm{1}}}}}{{{{\rm{M}}_{\rm{2}}}}}\; = \frac{{3.60\cancel{M}\; \times \;{\rm{400}}{\rm{.0}}\;{\rm{mL}}}}{{0.350\;\cancel{M}}}\; = \;4,110\;{\rm{mL}}\;{\rm{ = }}\;{\rm{4}}{\rm{.11}}\;{\rm{L}}\]
We used the volumes in mL and convert them to liters at the end. However, you can also convert the volumes to liters first which will also help avoid potential mistakes because the units of molarity are mol/L.
Let’s do another example. Let’s say we have a concentrated 6.0 M solution of paint and need to prepare 2.0 L of a 0.45 molar solution. How many liters of the stock do we need?
First, assign the notation for the stock and final solutions, and list, the given data and the unknown together:
M1 = 6.0 M
M2 = 0.45 M
V2 = 2.0 L
_________________
V1 = ?
M1V1 = M2V2
\[{{\rm{V}}_{\rm{1}}}\;{\rm{ = }}\;\frac{{{{\rm{M}}_{\rm{2}}}{{\rm{V}}_{\rm{2}}}}}{{{{\rm{M}}_{\rm{1}}}}}\; = \frac{{0.45\cancel{M}\; \times \;{\rm{2}}{\rm{.0}}\;{\rm{L}}}}{{6.0\;\cancel{M}}}\; = \;0.15\;{\rm{L}}\]
So, we will add 0.15 L of the paint, and add some solvent to make the final volume of the solution to 2.0 L.
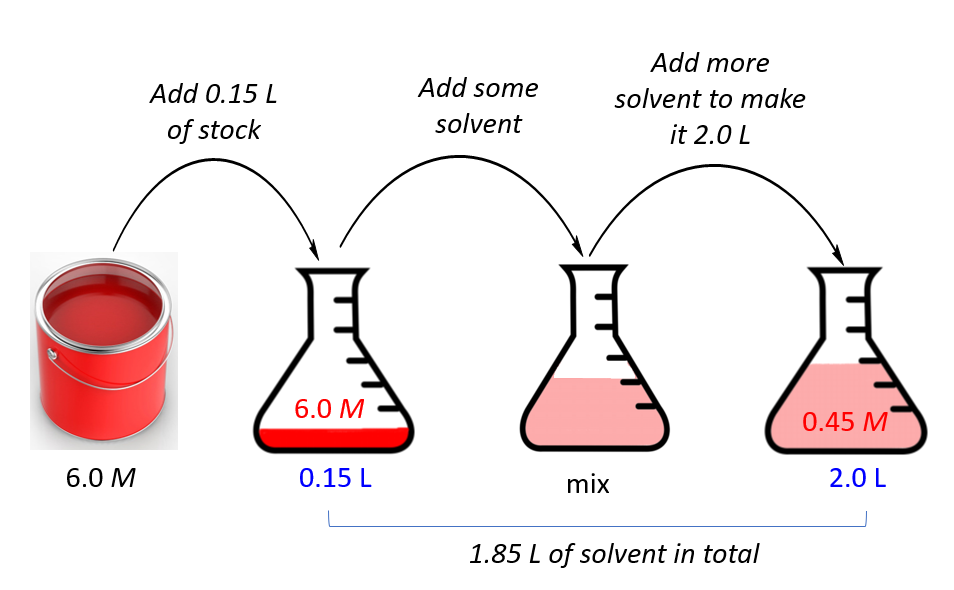
The volume of the solvent then is 2.0 – 0.15 = 1.85 L.
Check Also
- Solutions
- Strong and Weak Electrolytes
- Dissociation of Ionic Compounds
- Molecular, Ionic, and Net Ionic Equations
- Molarity
- Ion Concentration
- Precipitation Reactions
- Definitions of Acids and Bases
- Acid-Base Reactions
- Stoichiometry of Reactions in Aqueous Solutions
- Acid-Base Titrations
- Oxidation State
- Oxidation-Reduction (Redox) Reactions
- Reactions in Aqueous Solutions Practice Problems
Practice
How many mL of a concentrated solution of sodium chloride (4.00 M) must be diluted to 300.0 mL to prepare a 0.600 M solution?
How many liters of 0.350 molar sodium hydroxide solution can you prepare from 400.0 mL of 3.60 M solution of sodium hydroxide?
Calculate the molarity of the solution prepared by diluting 40.0 mL of 3.0 M KNO3 with 210.0 mL of water?
How many mL of a 2.00 molar MgCl2 stock solution and water are needed to prepare a 500. mL 0.400 M solution?
A student has 2.0 L of 7.0 M hydrochloric acid, HCl. She wants to prepare a 1.5 M solution. How many liters of solution can she make?
What is the concentration of the solution made by mixing 100. mL of 2.0 M and 250. mL 3.5 M solutions of potassium iodide?

Its is real good and cool I real love this. thank you developers God bless you all