We have seen in the previous post, that the Gibbs free energy of a reaction is a comprehensive measure of the spontaneity of the reaction that can be calculated based on the parameters of the system.
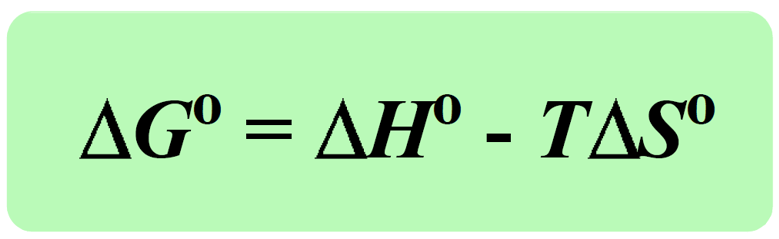
Today, we are going to see how the enthalpy, temperature, and entropy of the reaction affect the ΔGo. The first thing is you need to remember that a negative ΔGo indicates a spontaneous reaction, and a positive ΔGo indicates a nonspontaneous reaction:
♦ ΔG < 0: A negative ΔG corresponds to a spontaneous process.
♦ ΔG > 0: A positive ΔG corresponds to a nonspontaneous process.
♦ ΔG = 0: The system is at equilibrium. There is no net change.
Let’s first look at the big picture by isolating the two terms in the Gibbs free energy equation: the ΔHo and TΔSo terms:

To make the (more) process spontaneous, you want to make the ΔGo a negative large number. Therefore, a negative ΔHo, meaning an exothermic reaction, is a good contributor to making the reaction spontaneous. On the other hand, increasing the entropy makes the ΔGo smaller because of the negative sign and therefore, it also indicates a spontaneous reaction:
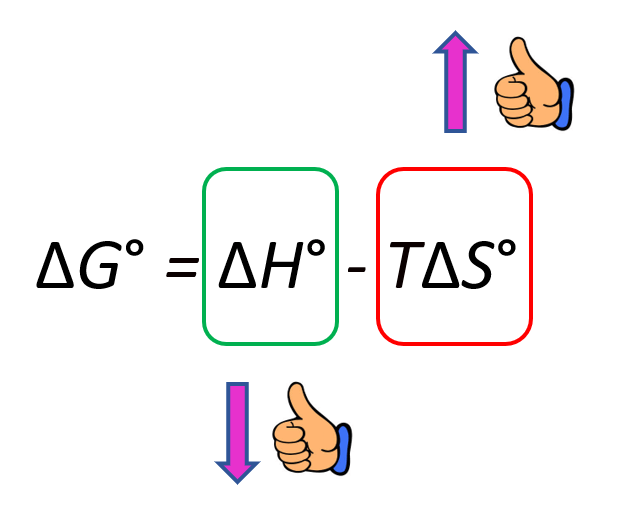
In general, there are four possibilities for the signs of the ΔHo and ΔSo which are summarized below:

Scenario 1. When ΔH is negative and ΔS is positive, ΔG is negative at all temperatures because regardless of the values, the net product is a negative number.
Therefore, we can state that exothermic reactions with a positive entropy change are always spontaneous.
Scenario 2. When ΔH is positive and ΔS is negative, ΔG is positive at all temperatures, and therefore, the reaction is nonspontaneous. This is expected because an endothermic reaction goes upwards energetically and decreasing the entropy makes the reaction less spontaneous too. To summarize, we can say that endothermic reactions with a negative entropy change are always nonspontaneous, regardless of the temperature.
Scenario 3. If both ΔH and ΔS are positive, then ΔG will be negative only when the T ΔS > H. Increasing the temperature will favor spontaneity as it makes the T ΔS a larger negative number because of the negative sign.
Scenario 4. If both ΔH and ΔS are negative, then ΔG will be negative only when the T ΔS < H. Decreasing the temperature will favor spontaneity as it makes the T ΔS a smaller positive number.
For example, given the values, ΔH°rxn = -18,000 J, and ΔS°rxn = -70 J/K, calculate the ΔG°rxn at 25 oC and determine if the reaction is spontaneous or not.
Solution:
ΔG°rxn = ΔH°rxn – TΔS°rxn = -18,000 J – (25 + 273) (-70 J/K) = 2,860 J
ΔG°rxn > 0, therefore, the process is nonspontaneous at 25 oC.
The temperature at Which the Reaction Becomes Spontaneous
Now, you need to know that if the reaction is not spontaneous at a given temperature, it does not mean it won’t be spontaneous at a different temperature. Sometimes, you may get a question on a test asking to determine the temperature at which a given reaction becomes spontaneous.
To do that, you need to first, set ΔG = 0 which corresponds to the equilibrium, and determine the corresponding temperature. This is the crossover temperature at which a reaction switches between being spontaneous and nonspontaneous and we derive it from the Gibbs free energy equation.
For example, at what temperature the reaction in the previous example will become spontaneous?
Solution: To find the temperature at which the reaction becomes spontaneous, first, set ΔG = 0 which corresponds to the equilibrium, and determine the corresponding temperature.
ΔG = ΔH – TΔS
0 = ΔH – TΔS
\[T\, = \,\frac{{\Delta H}}{{\Delta S}}\]
\[T{\mkern 1mu} = {\mkern 1mu} \frac{{\Delta H}}{{\Delta S}}\; = \;\frac{{18,000\,{\rm{J}}}}{{70\,{\rm{J/K}}}}\, = \;257\,{\rm{K}}\,\]
Next, identify the favorable term that makes ΔG negative. In this case, ΔH is the favorable term because it is negative and therefore, it decreases the ΔG. Because the entropy is negative, TΔSorxn is positive, we need to make the TΔSorxn a less significant contributor by decreasing the temperature. It means the process will become spontaneous below 257 K.
Note: If the ΔHorxn and ΔSorxn are not given in the problem, you need to calculate them first, using the data in the appendix, and then plug the values in the Gibbs free energy equation.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Gibbs Free Energy
- Entropy and State Change
- Entropy Changes in the Surroundings
- 𝚫Gorxn from the Free Energies of Formation
- Gibbs Free Energy and Hess’s Law
- Gibbs Free Energy Under Nonstandard Conditions
- Gibbs Free Energy and Equilibrium Constant
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
Practice
Given the values of ΔH and ΔS, which of the following changes will be spontaneous at constant T and P?
a) ΔH = +35 kJ, ΔS = +10 J/K, T = 300. K
b) ΔH = +45 kJ, ΔS = +153 J/K, T = 312 K
c) ΔH = – kJ, ΔS = +8.0 J/K, T = 298 K
d) ΔH = – kJ, ΔS = -60. J/K, T = 250 K
At what temperatures will the following processes be spontaneous?
a) ΔH = +25.0 kJ, ΔS = +40.0 J/K
b) ΔH = -5.00 kJ, ΔS = -30.0 J/K
c) ΔH = -20.0 kJ, ΔS = +60.0 J/K
c) ΔH = +45.0 kJ, ΔS = -70.0 J/K
