Chemical Thermodynamics

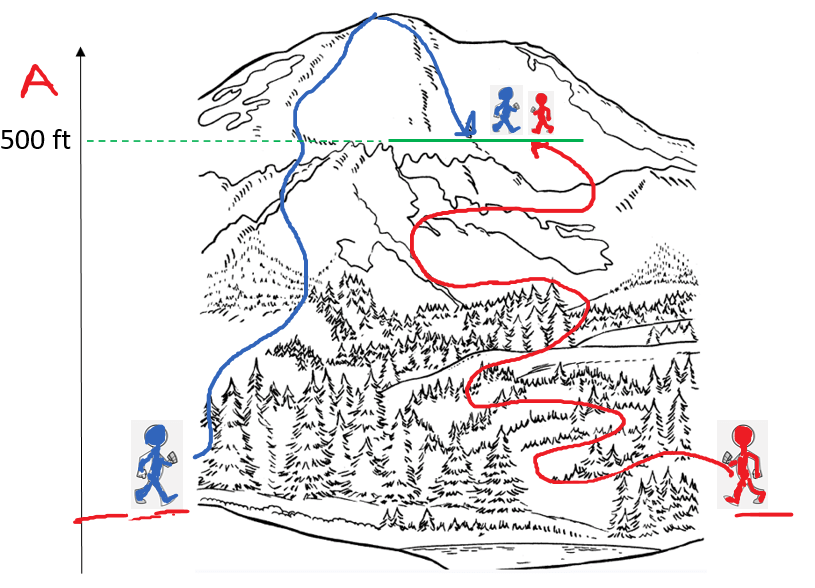
Because entropy is a state function, we can calculate the entropy change of a reaction if we know the standard entropies, So of the reactants and products. Remember, a state function depends only on the initial and final values and not on the path that leads to these states. A classic example of a state function is attitude. Regardless of the path the hikers have taken, they both are at the same altitude:

 

 

The standard entropy change of the reaction is calculated by subtracting the standard entropies of the reactants multiplied by their stoichiometric coefficients from the standard entropies of the products multiplied by their stoichiometric coefficients:

 

 

The standard entropies of reactants and products are given in textbooks under the appendix for thermodynamics data.

 

This is similar to how we calculate the enthalpy of a reaction from the standard enthalpies of formation.

Notice, however, that So, unlike ΔHo f and ΔGof for elements is not zero at 25 °C

 

For example, using the data in an appendix for homonymic data, calculate the standard entropy changes, ΔS for the following reactions at 25°C:

 

2H2S(g) + 3O2(g)  → 2SO2(g) + 2H2O(l)

 

The standard entropies of formation, S° (J/K) for the reactants and products are: H2S(g) = 205.8, for O2(g) = 205.2, for SO2(g) = 248.2, for H2O(l) = 70

 

Therefore, the standard entropy change for the reaction is:

 

ΔS°rxn = [2 x S° (H2O) + 2 x S° (SO2)] – [2 x S° (H2S) + 3 x S°(O2)]

ΔS°rxn = [2 x 70 J/K + 2 x 248.2 J/K] – [2 x 205.8 J/K + 3 x 205.2 J/K] = -390.8 J/K

 

Check Also

Practice

1.

Using the data in the attached Appendix, calculate the standard entropy changes, ΔS for the following reactions at 25°C:

 

a) 2KO2(aq)+ 2H2O(l) → 2KOH(aq) + O2(g)+ H2O2(l)

b) C2H5OH(l) + 3O2(g) → 2CO2(g) + 3H2O(g)

c) C2H4(g) + H2(g) → C2H6(g)

d) C(s)graphite + H2O(g) → CO(g) + H2(g)

e) 3NO2(g) + H2O(l) → 2HNO3(aq) + NO(g)

f) 2H2S(g) + 3O2(g) → 2H2O(l) + 2SO2(g)

g) N2O(g) + 3H2(g) → N2H4(l) + H2O(l)

h) 2C3H7OH(l) + 9O2(g) → 6CO2(g) + 8H2O(l)

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
e)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
f)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
g)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
h)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  

Leave a Comment

error: Content is protected !!