Percentage composition shows the amount of each element in a compound expressed as a mass percent.

To calculate the percentage of an element, multiply its molar mass and the subscript which shows how many moles of it are present in one mole of the compound, then divide the product by the molar mass of the compound.

For example, let’s determine the percent composition of sulfuric acid (H₂SO₄). If the element is not specified, we need to calculate the percentage of all the elements.

The molar mass of sulfuric acid is: M (H₂SO₄) = 2 x 1.0 + 32 + 4 x 16.0 = 98 g/mol.

\[{\rm{\% }}\;{\rm{(H)}}\;{\rm{ = }}\;\frac{{{\rm{2}}\;{\rm{ \times }}\,{\rm{M}}\,{\rm{(H)}}}}{{{\rm{M}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}}\;{\rm{ = }}\;\frac{{{\rm{2}}\,{\rm{ \times }}\,{\rm{1}}{\rm{.0}}\,}}{{{\rm{98}}\,}}\,{\rm{ \times }}\,100\% \; = \;2.0\% \]

\[{\rm{\% }}\;{\rm{(S)}}\;{\rm{ = }}\;\frac{{{\rm{M}}\,{\rm{(S)}}}}{{{\rm{M}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}}\;{\rm{ = }}\;\frac{{{\rm{32}}{\rm{.1}}\,}}{{{\rm{98}}\,}}\,{\rm{ \times }}\,100\% \; = \;33\% \]

\[{\rm{\% }}\;{\rm{(O)}}\;{\rm{ = }}\;\frac{{{\rm{4}}\;{\rm{ \times }}\,{\rm{M}}\,{\rm{(O)}}}}{{{\rm{M}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}}\;{\rm{ = }}\;\frac{{{\rm{4}}\,{\rm{ \times }}\,{\rm{16}}\,}}{{{\rm{98}}\,}}\,{\rm{ \times }}\,100\% \; = \;65\% \]

The sum of the percentages of all elements in the compound is 100%, so you can find the last one by subtracting the sum of the other elements from 100. This relies on the accuracy of the previous calculations, so double-check your calculation!

For example, let’s determine the percent composition of ammonia (NH₃).

\[{\rm{\% }}\;{\rm{(H)}}\;{\rm{ = }}\;\frac{{{\rm{3}}\;{\rm{ \times }}\,{\rm{M}}\,{\rm{(H)}}}}{{{\rm{M}}\;{\rm{(N}}{{\rm{H}}_{\rm{3}}}{\rm{)}}}}\;{\rm{ = }}\;\frac{{{\rm{3}}\,{\rm{ \times }}\,{\rm{1}}{\rm{.0}}\,}}{{{\rm{17}}\,}}\,{\rm{ \times }}\,100\% \; = \;17.6\% \]

Therefore, nitrogen makes 100 – 17.6 = 82.4% of ammonia by mass.

Empirical Formula

The empirical formula of a compound indicates the mole ratio of atoms in the simplest whole numbers. For example:

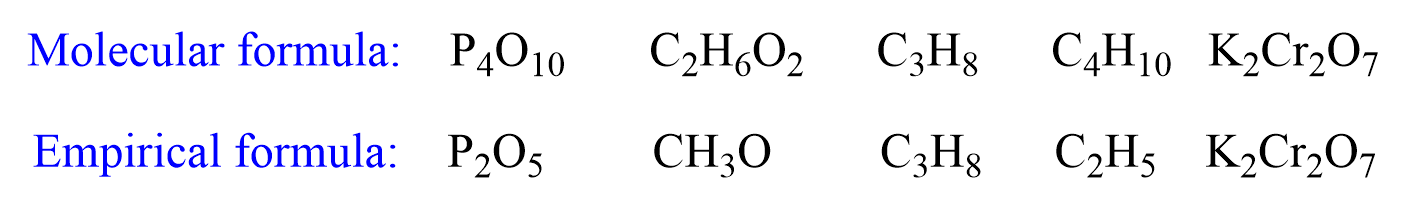
Notice that the empirical formula can be the same as the molecular formula if the numbers cannot be simplified any further.

Determining the Empirical and Molecular Formulas

To determine the empirical and molecular formulas, given the mass or percentage of the elements, you need to convert them to moles. This is because, remember, the formula of a compound tells us how many moles of each element there are in one mole of that compound.

For example, the formula of fructose C₆H₁₂O₆ indicates that in one mole of fructose, there are six moles of carbon, twelve moles of hydrogen, and six moles of oxygen.

Therefore, if you are asked to determine the empirical or molecular formula of a compound, you need to find the moles of each element.

For example, What are the empirical and molecular formulas of ascorbic acid if it consists of 40.92% carbon (C), 4.58% hydrogen (H), and 54.50% oxygen (O) and the molar mass is 176.1 g/mol?

The quantities are given in percentage, so we’ll go ahead and write these numbers as subscripts in the formula and convert them to moles following the steps in this plan:

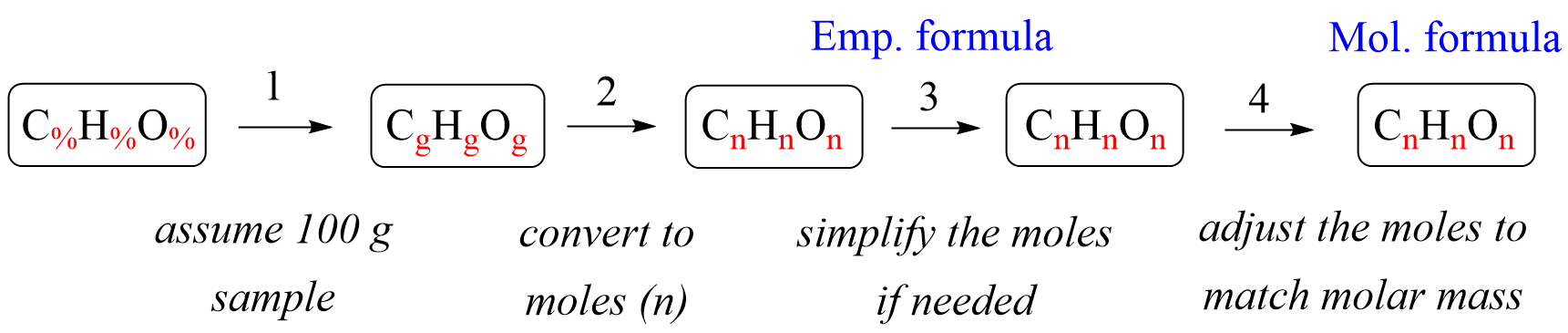
1) The first step is converting the % to mass, and you may be wondering how to achieve this transformation. Remember, whenever the quantities are not given or not relatable, you can assume a certain amount of the compound because whether it is, for example, 100 g or 450 g of water, the formula is always the same.

Now, when going from % to mass, the easiest is to assume a 100 g sample since this converts to units from % to grams without changing the numbers. So, assuming a 100 g sample, we have 40.92% g C, 4.58% g H, and 54.50% g O.

2) Find the moles of C, H, and O using their molar masses:

\[{\rm{n}}\;{\rm{(C)}}\;{\rm{ = }}\,\frac{{{\rm{m}}\;}}{{{\rm{M}}\;}}\,{\rm{ = }}\;\frac{{{\rm{40}}{\rm{.92}}\;{\rm{g}}\;}}{{{\rm{12}}{\rm{.0}}\;{\rm{g/mol}}\;}}\;{\rm{ = }}\,{\rm{3}}{\rm{.41}}\;{\rm{mol}}\]

\[{\rm{n}}\;{\rm{(H)}}\;{\rm{ = }}\,\frac{{{\rm{m}}\;}}{{{\rm{M}}\;}}\,{\rm{ = }}\;\frac{{{\rm{4}}{\rm{.58}}\;{\rm{g}}\;}}{{{\rm{1}}{\rm{.00}}\;{\rm{g/mol}}\;}}\;{\rm{ = }}\,{\rm{4}}{\rm{.58}}\;{\rm{mol}}\]

\[{\rm{n}}\;{\rm{(C)}}\;{\rm{ = }}\,\frac{{{\rm{m}}\;}}{{{\rm{M}}\;}}\,{\rm{ = }}\;\frac{{{\rm{54}}{\rm{.50}}\;{\rm{g}}\;}}{{{\rm{16}}{\rm{.0}}\;{\rm{g/mol}}\;}}\;{\rm{ = }}\,{\rm{3}}{\rm{.41}}\;{\rm{mol}}\]

Don’t worry about significant figures here and keep at least three decimals.

3) Dividing the numbers by the smallest one is usually a good start to simplifying them. So, dividing by 3.41, the moles are:

C₁H_1.343O₁

 We still need to simplify the moles of H. Remember, you can divide or multiply by any number to get a set of the simplest integers. Multiplying 1.343 by 3 is 4.029, which is approximately equal to 4 (4.029 ≈ 4). Make sure to multiply all the subscripts – you cannot multiply only one and leave the others because that would change the mole ratio of the elements. Therefore, by multiplying all the subscripts by 3, we get that the empirical formula is

C₃H₄O₃

4) Next, we need to check if the empirical formula is the same as the molecular formula of the compound. For this, calculate the molar mass of the empirical formula C₃H₄O₃, to see if it matches the actual molar mass given in the problem (176.1 g/mol):

3 x 12.0 + 4 x 1.00 + 3 x 16.0 = 88 g/mol

This indicates that the empirical formula of this compound is not the same as its molecular formula.

Divide 176.1 by 88 to see how many times larger the molar mass of the molecular formula is compared to the one of the empirical formula:

176.1/88 ≈ 2

Therefore, the subscripts (moles) in the empirical formula must be multiplied by two to obtain the molecular formula:

molecular formula = 2 x empirical formula

2 x C₃H₄O₃ = C₆H₈O₆

Calculate the molar mass of this formula to make sure it matches the one given in the problem:

M (C₆H₈O₆) = 6 x 12.0 + 8 x 1.00 + 6 x 16.0 = 176 g/mol

Check Also

• The Mole and Molar Mass
• Molar Calculations
• Percent Composition and Empirical Formula
• Stoichiometry of Chemical Reactions
• Limiting Reactant
• Reaction/Percent Yield
• Stoichiometry Practice Problems