First, we need to draw the Lewis structure of CO2.
In short, these are the steps you need to follow for drawing a Lewis structure:
1. Write the correct skeletal structure for the molecule.
* Hydrogen atoms are always terminal (only one bond)
* Put more electronegative elements in terminal positions
2. Sum the valence electrons from all the atoms.
3. Use a pair of electrons to form a bond between each pair of bound atoms.
4. Add the remaining electrons to satisfy the octet for a more electronegative atom first.
5. If any atoms lack an octet, make a double or triple bond to give them an octet.
Oxygen being more electronegative goes on the periphery:
![]()
For the valence electrons, we have 4 from the carbon and 2 x 6 = 12 from two oxygens, giving 16 valence electrons in total:

One bond between the carbon and each oxygen takes 4 electrons and we have 12 electrons left:

Place 6 on each oxygen and check for the octets:

The oxygens have 8 electrons. However, the carbon has only four and in these cases, you need to move one of the lone pairs, from the element that has an octet to the element lacking an octet to make another bond:

The same is done for the other carbon since it still lacks an octet:

At this point, all the atoms have 8 electrons. Notice that there are four electrons between the carbon and each oxygen which means they make two double bonds:

The steric number of carbon is two – two atoms, with no lone pairs, and therefore, the hybridization is sp.
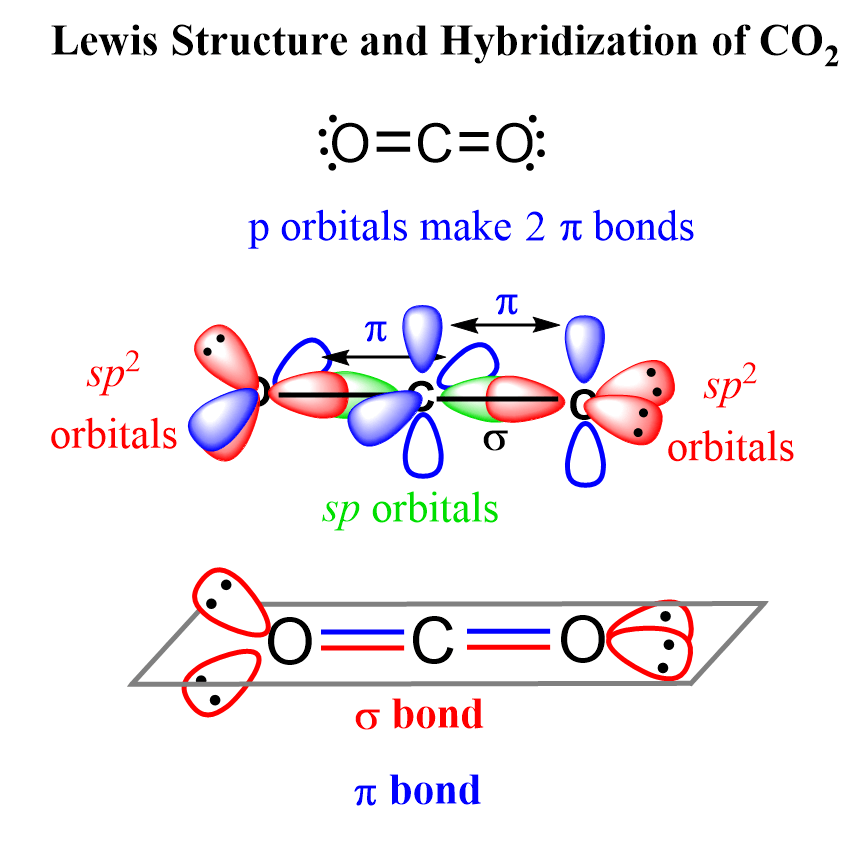
The sigma bond with each oxygen is formed by the linear overlap of the C(sp) and O(sp2) orbitals, while the pi bonds are formed by a side-to-side orbital overlap of the unhybridized p orbitals of the carbon and oxygens.
An interesting feature about this geometry is that the sp2 orbitals, containing the lone pairs of the oxygens, are at 90o because the unhybridized p orbitals of carbon are also oriented 90° to each other, and in order the overlap make the pi bonds, the p orbitals must be parallel.
Check this 99-question multiple-choice quiz on Geometry and Hybridization:
Check Also

