Because free energy, G is a state function, we can calculate the free energy change of a reaction, ΔGorxn by subtracting the free energies of the reactants of the reaction from the free energies of the products of the reaction.
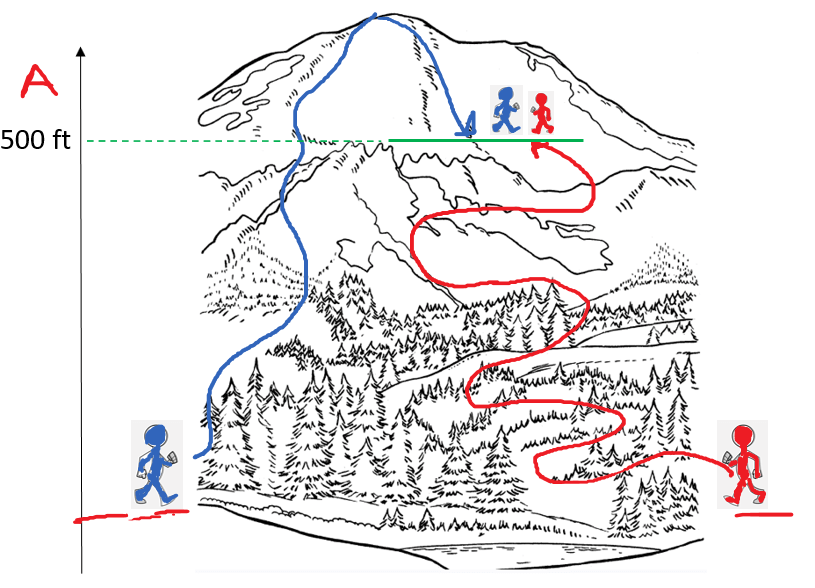
Remember, a state function depends only on the initial and final values and not on the path that leads to these states. A classic example of a state function is attitude. Regardless of the path the hikers have taken, they both are at the same altitude:
The standard free energy change of the reaction is calculated by subtracting the standard free energies of formation of the reactants multiplied by their stoichiometric coefficients from the standard free energies of formation of the products multiplied by their stoichiometric coefficients:

The standard free energy of formation of a compound, ΔGof is the free-energy change that occurs when 1 mole of the compound is synthesized from its elements in their standard states. This is similar to the definition of standard enthalpies of formation that we used to calculate the enthalpy of a reaction.
- The standard free energy of formation and products are given in textbooks under the appendix for thermodynamics data.
- Like the standard enthalpy of formation, ΔHof, ΔGof for elements is equal to zero at 25 °C.
For example, given the values of ΔGof, calculate ΔG°rxn for the following reaction at 25°C:
2C2H6(g) + 7O2(g) → 4CO2(g) + 6H2O(l)
Solution: To calculate 𝚫G°rxn, we need to subtract the standard free energies of formations of the reactants from the standard free energies of formations of products, both multiplied by their stoichiometric coefficients:
ΔG°rxn = ΣnpΔGof (products) – ΣnrΔGof (reactants)
where np and nr are the molar coefficients of the products and reactants in the balanced chemical equation
Remember, the standard free energies of formations of elements or their molecules in standard states are equal to zero.
From an appendix for thermodynamic data, we find that:
ΔGf° (kJ/mol): for C2H6(g) = -46.2, for O2(g) = 0, for CO2(g) = -394.4, for H2O(l) = -237.2
We can now enter the numbers to determine the heat of our reaction:
ΔG°rxn = [6 x Gf° (H2O) + 4 x Gf° (CO2)] – [2 x Gf° (C2H6) + 7 x Gf° (O2)]
ΔG°rxn = [6 x (-237.2 kJ) + 4 x (-394.4)] – [2 x (-32.89 kJ) + 7 x 0] = -2935 kJ/mol
As already mentioned, another way of determining the standard free energy change of a reaction is using the Gibbs free energy equation.
Which equation you need to use, depends largely on which one you can use. In some problems, it will be mentioned which one to use, in some, you will need to go based on the data given.
For example, this equation, ΔG°rxn = ΣnpΔGof (products) – ΣnrΔGof (reactants), is not suitable for calculating the free energy charge of reactions at higher temperatures because the values of ΔGof are usually given for 25 oC.
Instead, we use the Gibbs free energy formula correlating ΔG° with ΔH° and ΔS°:
ΔG° = ΔH° – TΔS°
You may ask how come we can use the tabulated values of ΔH°f and S° but not Gof.
The reason is that although the enthalpies and entropies are affected by temperature, the difference between their values is very little compared to the temperature change. As a result, the values of ΔH° and ΔS° do not change much with temperature. However, ΔG° is more sensitive to temperature which we can see by the presence of T in the equation ΔG° = ΔH° – TΔS°.
Check Also
- Standard Entropy Change (𝚫Sorxn) of a Reaction
- The Gibbs Free Energy
- The Effect of 𝚫H, 𝚫S, and T on 𝚫G – Spontaneity
- Entropy and State Change
- Entropy Changes in the Surroundings
- Gibbs Free Energy and Hess’s Law
- Gibbs Free Energy Under Nonstandard Conditions
- Gibbs Free Energy and Equilibrium Constant
- Entropy, Enthalpy, and Gibbs Free Energy Practice Problems
Practice
Using the data for standard free energies of formations in the attached appendix, calculate the standard free energy of each reaction at 25 oC.
a) 6Cl2(g) + 2Fe2O3(s) → 4FeCl3(s) + 3O2(g)
b) 2CH3OH(g) + H2(g) → C2H6(g) + 2H2O(g)
c) Fe2O3(s) + 3CO(g) → 2Fe(s) + 3CO2(g)
